�o�Ȑ��@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�W���`�F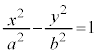 �C
�C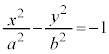 �@(
�@(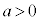 �C
�C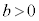 )
)
�o�Ȑ��̒�`�F2��_(�œ_�ƌ���)����̋����̍������ł���_�̏W�����o�Ȑ��ƌ����B
�o�Ȑ��́A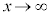 �C
�C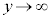 �Ƃ���ƁA����Ȃ��Q�ߐ��ɐڋ߂��Ă����B�W���`�ŗ^������o�Ȑ��̏ꍇ�A�Q�ߐ��́A
�Ƃ���ƁA����Ȃ��Q�ߐ��ɐڋ߂��Ă����B�W���`�ŗ^������o�Ȑ��̏ꍇ�A�Q�ߐ��́A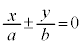
���ɁA�Q�ߐ�����������o�Ȑ����A���p�o�Ȑ��ƌ����B
�o�Ȑ��̒�`����A�o�Ȑ��̕������̕W���`���Ă݂܂��B
2�œ_���AF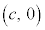 �C
�C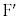
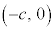 �C2�œ_�܂ł̋����̍���
�C2�œ_�܂ł̋����̍���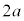 (
(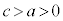 )�Ƃ��܂��B
)�Ƃ��܂��B
�o�Ȑ���̓_P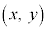 ��2�œ_�܂ł̋����̍��́A
��2�œ_�܂ł̋����̍��́A
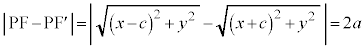
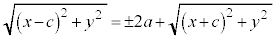
���ӂ�2�悷��ƁA
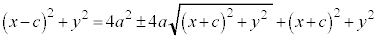
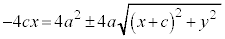
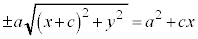
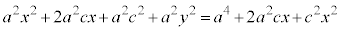
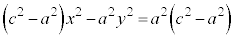
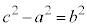 �@����@�@�Ƃ����āA���ӂ�
�@����@�@�Ƃ����āA���ӂ�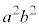 �Ŋ���ƁA
�Ŋ���ƁA
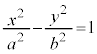
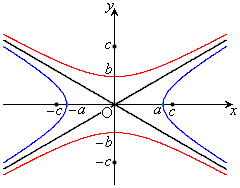 �����ŁA
�����ŁA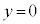 �Ƃ���ƁA
�Ƃ���ƁA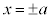
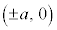 ��o�Ȑ������_�ƌ����܂��B
��o�Ȑ������_�ƌ����܂��B
�@�����A�o�Ȑ��F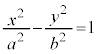 �̏œ_�̍��W
�̏œ_�̍��W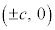 �ɂ��āA
�ɂ��āA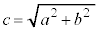 �@(�E�}���Q��)
�@(�E�}���Q��)
�o�Ȑ��̏œ_��y����ɂ���ꍇ�ɂ́A2�œ_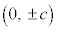 ����̋����̍���
����̋����̍���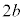 ���Ƃ��āA�o�Ȑ��̕������́A
���Ƃ��āA�o�Ȑ��̕������́A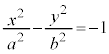 �ɂȂ�܂�(x�Ca�̗����y�Cb�̗��ꂪ���ꊷ���Ǝv���悢�B�E�}�Ԑ��Q��)�B���̂Ƃ��ɂ��A
�ɂȂ�܂�(x�Ca�̗����y�Cb�̗��ꂪ���ꊷ���Ǝv���悢�B�E�}�Ԑ��Q��)�B���̂Ƃ��ɂ��A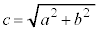 �ƂȂ�܂��B
�ƂȂ�܂��B
�o�Ȑ��̕������F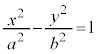 �C
�C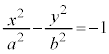 �����_
�����_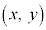 �ɑ��āAx�̂Ƃ����
�ɑ��āAx�̂Ƃ����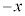 �������Ă��Ay�̂Ƃ����
�������Ă��Ay�̂Ƃ����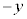 �������Ă��A�o�Ȑ��̕������͐��藧���܂��B�Ƃ������Ƃ́A�o�Ȑ��́Ax���Ɋւ��Ă��Ay���Ɋւ��Ă��A���_�Ɋւ��Ă��Ώ̂��Ƃ������Ƃł��B
�������Ă��A�o�Ȑ��̕������͐��藧���܂��B�Ƃ������Ƃ́A�o�Ȑ��́Ax���Ɋւ��Ă��Ay���Ɋւ��Ă��A���_�Ɋւ��Ă��Ώ̂��Ƃ������Ƃł��B
�o�Ȑ��̕������F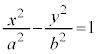 �ɂ����āA
�ɂ����āA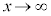 �C
�C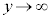 �Ƃ����Ƃ��A�E�ӂ�1�����ΓI�ɏ������Ȃ�̂ŁA�o�Ȑ���
�Ƃ����Ƃ��A�E�ӂ�1�����ΓI�ɏ������Ȃ�̂ŁA�o�Ȑ���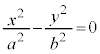 �ɋ߂Â����ƂɂȂ�A
�ɋ߂Â����ƂɂȂ�A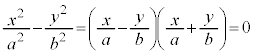 ���A�o�Ȑ��́A�Q�ߐ��F
���A�o�Ȑ��́A�Q�ߐ��F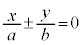 �����Ɨ������Ă����Ƃ悢�ł��傤�B
�����Ɨ������Ă����Ƃ悢�ł��傤�B
���m�ɂ́A�o�Ȑ��̕������F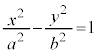 ��y�ɂ��ĉ����āA
��y�ɂ��ĉ����āA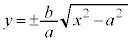
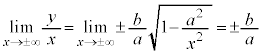 ���A�Q�ߐ��̌X���́A
���A�Q�ߐ��̌X���́A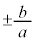
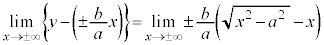
�@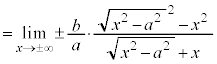
�@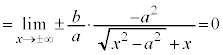
���A�Q�ߐ���y�ؕЂ�0
����āA�Q�ߐ��́A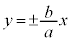
�o�Ȑ��F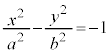 �̑Q�ߐ������l�ɁA
�̑Q�ߐ������l�ɁA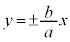 �ł��B
�ł��B
�o�Ȑ��F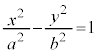 �ɐڂ���X��m�̐ڐ������߂Ă݂܂��B
�ɐڂ���X��m�̐ڐ������߂Ă݂܂��B
�o�Ȑ��̕�������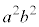 �������āA
�������āA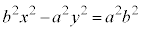
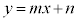 �ƘA�����āA
�ƘA�����āA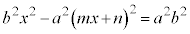
�������āA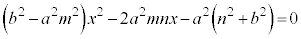
����2���������͏d���������܂�(2���������̈�ʘ_���Q��)�B
����āA���ʎ��F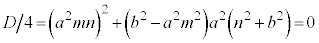
��������ƁA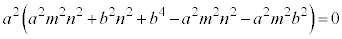
�� 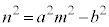
�� 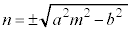
����ċ��߂�X��m�̐ڐ��́A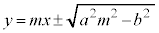
�o�Ȑ��̕������F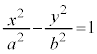 �̗��ӂ��A���̔����@�Ŕ�������ƁA
�̗��ӂ��A���̔����@�Ŕ�������ƁA
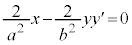
�� 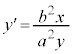
�o�Ȑ���̓_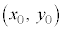 �ɂ�����ڐ��̌X���́A
�ɂ�����ڐ��̌X���́A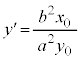
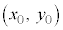 �ɂ�����ڐ��́A
�ɂ�����ڐ��́A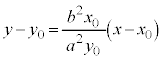
�� 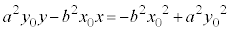 �@����A
�@����A
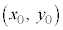 �͑o�Ȑ���̓_�Ȃ̂ŁA
�͑o�Ȑ���̓_�Ȃ̂ŁA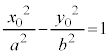 �����̂ŁA�A����
�����̂ŁA�A����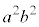 �Ŋ��邱�Ƃɂ��A
�Ŋ��邱�Ƃɂ��A
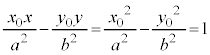
����āA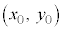 �ɂ�����ڐ��́A
�ɂ�����ڐ��́A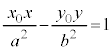
�o�Ȑ��F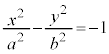 ��
��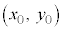 �ɂ�����ڐ������l�ɁA
�ɂ�����ڐ������l�ɁA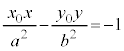 �ł��B
�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 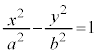 �C
�C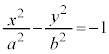 �@
�@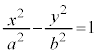 �C
�C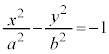 �@(
�@(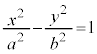
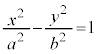 �̏œ_�̍��W
�̏œ_�̍��W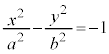 �ɂȂ�܂�(x�Ca�̗����y�Cb�̗��ꂪ���ꊷ���Ǝv���悢�B�E�}�Ԑ��Q��)�B���̂Ƃ��ɂ��A
�ɂȂ�܂�(x�Ca�̗����y�Cb�̗��ꂪ���ꊷ���Ǝv���悢�B�E�}�Ԑ��Q��)�B���̂Ƃ��ɂ��A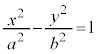 �C
�C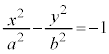 �����_
�����_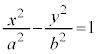 �ɂ����āA
�ɂ����āA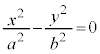 �ɋ߂Â����ƂɂȂ�A
�ɋ߂Â����ƂɂȂ�A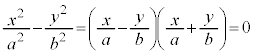 ���A�o�Ȑ��́A�Q�ߐ��F
���A�o�Ȑ��́A�Q�ߐ��F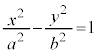 ��y�ɂ��ĉ����āA
��y�ɂ��ĉ����āA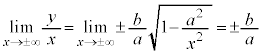 ���A�Q�ߐ��̌X���́A
���A�Q�ߐ��̌X���́A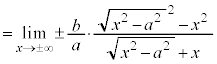
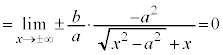
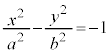 �̑Q�ߐ������l�ɁA
�̑Q�ߐ������l�ɁA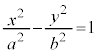 �ɐڂ���X��m�̐ڐ������߂Ă݂܂��B
�ɐڂ���X��m�̐ڐ������߂Ă݂܂��B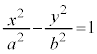 �̗��ӂ��A���̔����@�Ŕ�������ƁA
�̗��ӂ��A���̔����@�Ŕ�������ƁA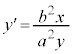
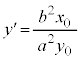
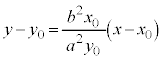
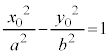 �����̂ŁA�A����
�����̂ŁA�A����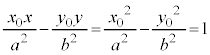
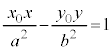
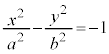 ��
��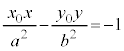 �ł��B
�ł��B