2���������̈�ʘ_�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
2���������F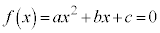 (
(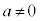 )���l���܂��B
)���l���܂��B
������������ƁA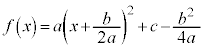
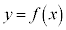 �̃O���t�́A
�̃O���t�́A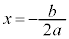 �����Ƃ��A
�����Ƃ��A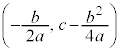 �_�Ƃ���������ɂȂ�܂�(2�����Q��)�B
�_�Ƃ���������ɂȂ�܂�(2�����Q��)�B
���_��x���W�Cy���W��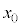 �C
�C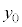 �Ƃ����܂��B
�Ƃ����܂��B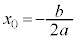 �C
�C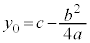 �ł��B
�ł��B
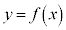 �̃O���t�̒��_�ƁA2���������F
�̃O���t�̒��_�ƁA2���������F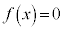 �̔��ʎ��F
�̔��ʎ��F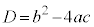 �Ƃ̊Ԃɂ́A
�Ƃ̊Ԃɂ́A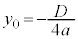 �Ƃ����W������܂��B
�Ƃ����W������܂��B
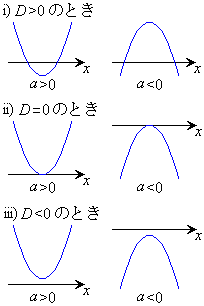 i)
i) 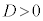 �̂Ƃ�
�̂Ƃ�
�E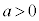 �Ȃ�O���t�͉��ɓʂ�
�Ȃ�O���t�͉��ɓʂ�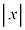 ��傫�����čs���ƁA
��傫�����čs���ƁA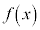 �̒l�͐��̒l�Ƃ��Ăǂ�ǂ�傫���Ȃ��Ă����܂��B
�̒l�͐��̒l�Ƃ��Ăǂ�ǂ�傫���Ȃ��Ă����܂��B
�@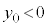 �Ȃ̂ŁA
�Ȃ̂ŁA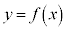 �̃O���t��x���ƕK��2��_�������܂��Bx���Ƃ̌�_��x���W��2���������F
�̃O���t��x���ƕK��2��_�������܂��Bx���Ƃ̌�_��x���W��2���������F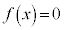 �̉��ł��B
�̉��ł��B
�@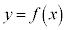 �̃O���t�͎��Ɋւ��đΏ̂Ȃ̂ŁAx���Ƃ̌�_�����ɑ��đΏ̂Ȉʒu��2����܂��B
�̃O���t�͎��Ɋւ��đΏ̂Ȃ̂ŁAx���Ƃ̌�_�����ɑ��đΏ̂Ȉʒu��2����܂��B
�@�]���āA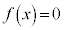 �̉��́A
�̉��́A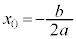 �ɁA���鐳�̒l���v���X�E�}�C�i�X�������̂ɂȂ�A
�ɁA���鐳�̒l���v���X�E�}�C�i�X�������̂ɂȂ�A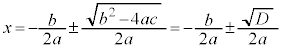 �@����@�@�ƂȂ�܂�(���̌���)�B
�@����@�@�ƂȂ�܂�(���̌���)�B
�E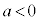 �Ȃ�O���t�͏�ɓʂ�
�Ȃ�O���t�͏�ɓʂ�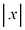 ��傫�����čs���ƁA
��傫�����čs���ƁA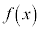 �̒l�͕��̒l�Ƃ��Đ�Βl���ǂ�ǂ�傫���Ȃ��Ă����܂��B
�̒l�͕��̒l�Ƃ��Đ�Βl���ǂ�ǂ�傫���Ȃ��Ă����܂��B
�@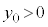 �Ȃ̂ŁA
�Ȃ̂ŁA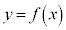 �̃O���t��x���ƕK��2��_�������܂��B
�̃O���t��x���ƕK��2��_�������܂��B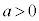 �̂Ƃ��Ɠ��l�ɁA����2��_�͎��Ɋւ��đΏ̂ŁA
�̂Ƃ��Ɠ��l�ɁA����2��_�͎��Ɋւ��đΏ̂ŁA
�@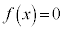 �̉��́A
�̉��́A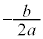 �ɁA���鐳�̒l���v���X�E�}�C�i�X�������̂ɂȂ�A
�ɁA���鐳�̒l���v���X�E�}�C�i�X�������̂ɂȂ�A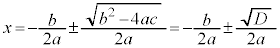 ����@�@�ƂȂ�܂��B
����@�@�ƂȂ�܂��B
ii) 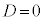 �̂Ƃ�
�̂Ƃ�
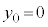 �ƂȂ�A
�ƂȂ�A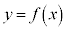 �̃O���t��x���Ɛڂ���悤�ɂȂ�܂��B�]���āA
�̃O���t��x���Ɛڂ���悤�ɂȂ�܂��B�]���āA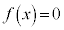 �̉���1��(�d��)
�̉���1��(�d��)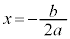 ��������܂���B
��������܂���B
�Ȑ��ƒ����A���邢�́A2�Ȑ��̌�������l����Ƃ��A���҂̕�������A������2����������������̂ł���A2���������̔��ʎ���0�ɂȂ邱�ƂƁA2�Ȑ����ڂ��邱�ƂƂ͓����Ӗ��������܂�(�u���l�v�ƌ����܂�)�B
iii) 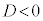 �̂Ƃ�
�̂Ƃ�
�E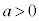 �Ȃ�
�Ȃ�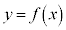 �̃O���t�͉��ɓʂ�
�̃O���t�͉��ɓʂ�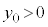 ���A�O���t��̑S�Ă̓_��x��������ɂ����āA�O���t��x���Ƌ��L�_�������܂���B
���A�O���t��̑S�Ă̓_��x��������ɂ����āA�O���t��x���Ƌ��L�_�������܂���B
�E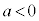 �Ȃ�
�Ȃ�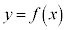 �̃O���t�͏�ɓʂ�
�̃O���t�͏�ɓʂ�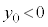 ���A�O���t��̑S�Ă̓_��x���������ɂ����āA�O���t��x���Ƌ��L�_�������܂���B
���A�O���t��̑S�Ă̓_��x���������ɂ����āA�O���t��x���Ƌ��L�_�������܂���B
�]���āAa�̐����ɂ�����炸�A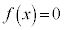 �͎������������܂���B
�͎������������܂���B
2����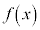 ���蕄���ł��邱�ƂƁA2��������
���蕄���ł��邱�ƂƁA2��������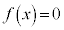 �̔��ʎ������ɂȂ邱�ƂƂ͓����Ӗ�(���l)�������܂��B
�̔��ʎ������ɂȂ邱�ƂƂ͓����Ӗ�(���l)�������܂��B
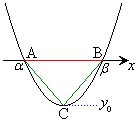 �E�}�̂悤�ɁA
�E�}�̂悤�ɁA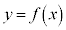 ��
��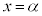 �C
�C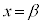 �ɂ�����x����2��_A�CB�����Ƃ��A
�ɂ�����x����2��_A�CB�����Ƃ��A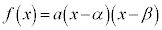 �ƈ�����������܂��B
�ƈ�����������܂��B
�@���A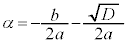 �C
�C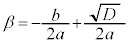 ���Ƃ��āA2��_�Ԃ̋���
���Ƃ��āA2��_�Ԃ̋���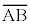 (2��������
(2��������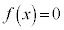 ��2���̍�)�́A
��2���̍�)�́A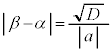
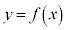 �̃O���t�̒��_��C�Ƃ��āA�O�p�`ABC�̍����A�����AC��x���Ƃ̋����́A
�̃O���t�̒��_��C�Ƃ��āA�O�p�`ABC�̍����A�����AC��x���Ƃ̋����́A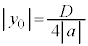
������A�O�p�`ABC�̖ʐς́A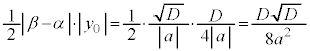 �ł��B
�ł��B
���ɁA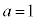 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A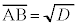 �C�O�p�`ABC�̖ʐς�
�C�O�p�`ABC�̖ʐς�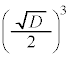 �ƂȂ�܂��B
�ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 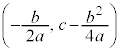 �_�Ƃ���������ɂȂ�܂�(2�����Q��)�B
�_�Ƃ���������ɂȂ�܂�(2�����Q��)�B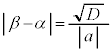
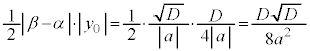 �ł��B
�ł��B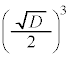 �ƂȂ�܂��B
�ƂȂ�܂��B