京大理系数学'13年[1]
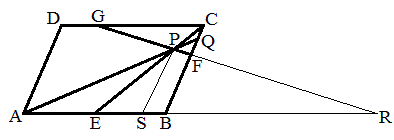
平行四辺形ABCDにおいて、辺ABを1：1に内分する点をE，辺BCを2：1に内分する点をF，辺CDを3：1に内分する点をGとする。線分CEと線分FGの交点をPとし、線分APを延長した直線と辺BCの交点をQとするとき、比AP：PQを求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 いくら易化傾向とは言っても、これでは標準的な高校入試問題です。高校3年間は何だったのか、と受験生に思われかねません。ベクトルを持ち出すまでもありませんね。
簡単にするために、
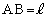とします。
直線GFと直線ABの交点をRとすると、
，
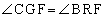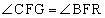より、△CGF∽△BRF
∴ CG：BR＝FC：FB＝1：2
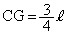より、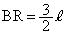
，
，
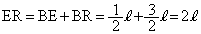
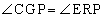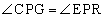より、△CGP∽△ERP
∴ PC：PE＝CG：ER＝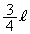
：
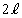＝3：8
Pを通り、BCに平行な直線と直線ABとの交点をSとすると、
ES：SB＝PE：PC＝8：3
∴ 
，
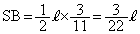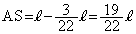
∴ AP：PQ＝AS：SB＝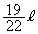
：
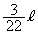＝19：3 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。