���嗝�n���w'99�N�O��[5]
�ȉ��̖₢�ɓ�����B�������A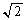 �C
�C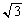 �C
�C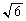 ���������ł��邱�Ƃ͎g���Ă悢�B
���������ł��邱�Ƃ͎g���Ă悢�B
(1) �L����p�Cq�Cr�ɂ��āA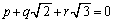 �Ȃ�A
�Ȃ�A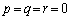 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (2) �����W����2����
�ɂ��āA �C
�C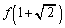 �C
�C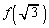 �̂����ꂩ�͖������ł��邱�Ƃ������B
�̂����ꂩ�͖������ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��֑�w�ł悭��������A�w���@��p����_�̖��ł��B
(2)�ł́Aa�Cb���u�����v�ƂȂ��Ă��邱�Ƃɒ��ӂ��܂��傤�BA�CB�������̏ꍇ�ɂ́A
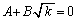 ��
�� 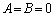
�܂��A����(��)�F
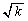 ���������̂Ƃ��A�L����A�CB���A
���������̂Ƃ��A�L����A�CB���A�����Ƃ��A
�����藧���Ƃ��ؖ����Ă����܂��B
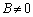 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA
�ƂȂ�A�E�ӂ͗L�����ŁA�������ƗL�������������Ƃ����s�������N���܂��B����āA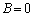 �ł���A
�ł���A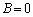 �Ȃ�
�Ȃ�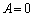 �ł��B
�ł��B
(1) 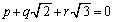 �@����@
�@����@ 2�悵�āA
 �C
�C �͗L�����Ȃ̂ŁA����(��)�ɂ��A
�͗L�����Ȃ̂ŁA����(��)�ɂ��A����āAp�Cq�̂ǂ��炩��0�ł��B
(i) 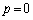 �̂Ƃ��A
�̂Ƃ��A �@���A
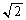 �������āA
�������āA �Cr�͗L�����Ȃ̂ŁA����(��)�ɂ��A
�Cr�͗L�����Ȃ̂ŁA����(��)�ɂ��A�܂�A �ł��B
�ł��B (ii)  �̂Ƃ��A
�̂Ƃ��A �@���A
q�Cr�͗L�����Ȃ̂ŁA����(��)�ɂ��A
�ȏ���A�L����p�Cq�Cr�ɂ��āA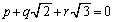 �Ȃ�A
�Ȃ�A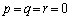
(2)  �C
�C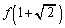 �C
�C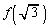 �����ׂėL�����ł���Ɖ��肵�܂��Bc�Cd�Ce��L�����Ƃ��āA
�����ׂėL�����ł���Ɖ��肵�܂��Bc�Cd�Ce��L�����Ƃ��āA ����a�Cb���c���Ă���ƁA����(��)�C���邢�́A(1)�̌��ʂ����p�ł��Ȃ��̂ŁAa�Cb��c�Cd�Ce�ŕ\�����Ƃ��l���܂��B���̂��߂ɁA�A�ƇC��a�Cb�Ɋւ���A���������ƌ��ĉ����܂��B
�C�|�A���A
�� 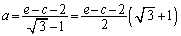 �@(�����L��������)�A���A
�@(�����L��������)�A���A �������B�ɑ������ƁA
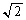 �������āA
�������āA(1)�̌��ʂ��g���ƁA �C
�C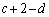 �C
�C �͗L�����Ȃ̂ŁA
�͗L�����Ȃ̂ŁA ������A
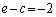 ����
���� 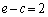
�Ƃ����������N���܂��B
����āA �C
�C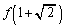 �C
�C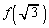 �����ׂėL�����ł���A�Ƃ�������͌��ŁA
�����ׂėL�����ł���A�Ƃ�������͌��ŁA
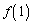 �C
�C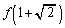 �C
�C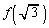 �̂����ꂩ�͖������ł��B
�̂����ꂩ�͖������ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B