関数の極限 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
関数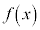 において、xがaと異なる値をとりながらaに限りなく近づくときに、
において、xがaと異なる値をとりながらaに限りなく近づくときに、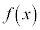 の値が限りなくαに近づくとします。
の値が限りなくαに近づくとします。
このとき、
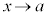 のとき、
のとき、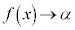
または、
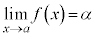
と書いて、αを極限値と言います。
関数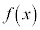 において、xがaと異なる値をとりながらaに限りなく近づくときに、
において、xがaと異なる値をとりながらaに限りなく近づくときに、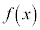 の値が限りなく大きくなるとします。
の値が限りなく大きくなるとします。
このとき、
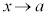 のとき、
のとき、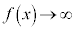
または、
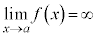
と書いて、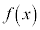 は正の無限大に発散する、と言います。
は正の無限大に発散する、と言います。
関数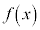 において、xがaと異なる値をとりながらaに限りなく近づくときに、
において、xがaと異なる値をとりながらaに限りなく近づくときに、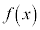 が負の値をとりながら、限りなく絶対値が大きくなるとします。
が負の値をとりながら、限りなく絶対値が大きくなるとします。
このとき、
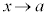 のとき、
のとき、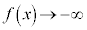
または、
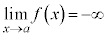
と書いて、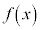 は負の無限大に発散する、と言います。
は負の無限大に発散する、と言います。
xが限りなく大きくなるときには、上記のaを正の無限大∞とします。
xが負の値をとりながら、その絶対値が限りなく大きくなるときには、上記のaを負の無限大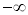 とします。
とします。
以上のいずれの場合についても、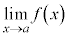 ,
,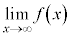 ,
,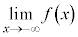 を極限と言います。
を極限と言います。
関数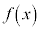 において、xが
において、xが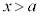 を満たしながらaに限りなく近づくときの極限を、
を満たしながらaに限りなく近づくときの極限を、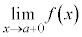 と書いて、右側極限、または、右方極限と言います。
と書いて、右側極限、または、右方極限と言います。
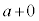 というのは、
というのは、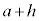 のhを0に近づけるという意味です。
のhを0に近づけるという意味です。
関数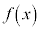 において、xが
において、xが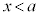 を満たしながらaに限りなく近づくときの極限を、
を満たしながらaに限りなく近づくときの極限を、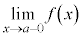 と書いて、左側極限、または、左方極限と言います。
と書いて、左側極限、または、左方極限と言います。
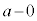 というのは、
というのは、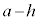 のhを0に近づけるという意味です。
のhを0に近づけるという意味です。
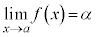 ⇔
⇔ 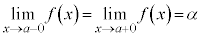
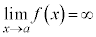 ⇔
⇔ 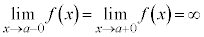
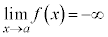 ⇔
⇔ 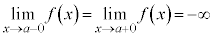
です。つまり、右側極限と左側極限が等しい場合にのみ、極限と言います。
右側極限と左側極限が一致しない場合には、極限とは言いません。
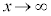 ,または、
,または、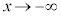 とするときに、
とするときに、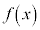 の値が1つの値に近づかないこともあります。このようなときには、
の値が1つの値に近づかないこともあります。このようなときには、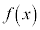 は振動すると言い、極限
は振動すると言い、極限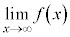 ,
,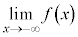 は存在しません。
は存在しません。
極限の性質
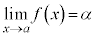 ,
,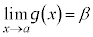 のとき、k,hを実数として、
のとき、k,hを実数として、
(線形性) 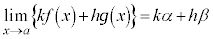
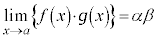
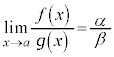 (但し、
(但し、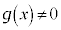 ,
,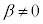 )
)
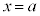 の近傍で
の近傍で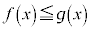 であれば、
であれば、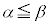
また、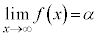 ,
,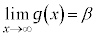 のとき、k,hを実数として、
のとき、k,hを実数として、
(線形性) 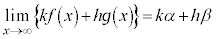
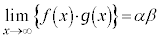
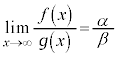 (但し、
(但し、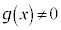 ,
,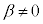 )
)
ある実数aについて、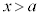 のとき
のとき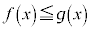 であれば、
であれば、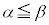
(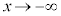 のときも同様)
のときも同様)
例1.a,bを実数として、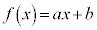 について、
について、 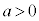 のとき、
のとき、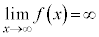 ,
,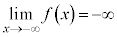 です。
です。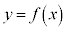 のグラフは右肩上がりの直線です。
のグラフは右肩上がりの直線です。
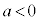 のとき、
のとき、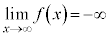 ,
,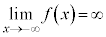 です。
です。 のグラフは右肩下がりの直線です。
のグラフは右肩下がりの直線です。
例2.a,b,cを実数として、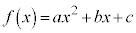 について、
について、 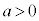 のとき、
のとき、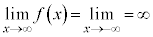 です。グラフは下に凸な放物線です。
です。グラフは下に凸な放物線です。
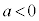 のとき、
のとき、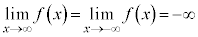 です。グラフは上に凸な放物線です。
です。グラフは上に凸な放物線です。
例3.一般的に、nが奇数,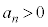 ,
,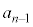 ,・・・,
,・・・,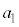 ,
,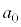 を実数として、
を実数として、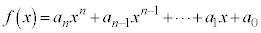 について、
について、 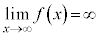 ,
,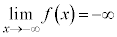 です。nが偶数,
です。nが偶数,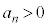 ,
,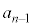 ,・・・,
,・・・,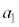 ,
,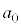 を実数として、
を実数として、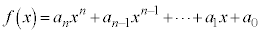 について、
について、
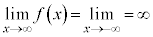 です。
です。
例4.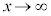 ,または、
,または、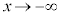 のとき、
のとき、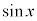 ,
,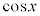 は振動するので、
は振動するので、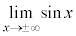 ,
,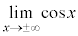 は存在しません。
は存在しません。
例7.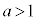 のとき、
のとき、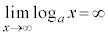 ,
,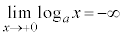
ですが、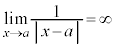 です。
です。
例9.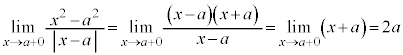
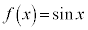
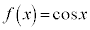
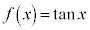
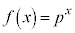 (
(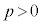 かつ
かつ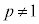 )のような関数では、任意の実数aについて、
)のような関数では、任意の実数aについて、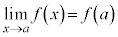 が成立します(関数の連続を参照)。
が成立します(関数の連続を参照)。
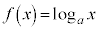 (
(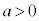 かつ
かつ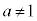 )の定義域は
)の定義域は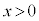 なので、任意の正数aについて、
なので、任意の正数aについて、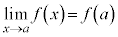 が成立します。
が成立します。
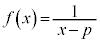 (pは実数)の定義域は
(pは実数)の定義域は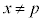 なので、
なので、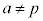 となる実数aについて、
となる実数aについて、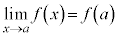 が成立します。
が成立します。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 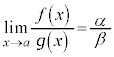 (但し、
(但し、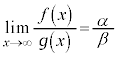 (但し、
(但し、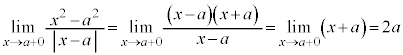
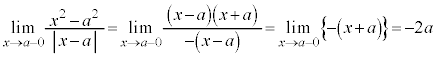
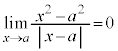 ですが、
ですが、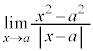 は存在しません。
は存在しません。