対数関数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
正数a,1以外の正数b,実数cに対して、 という関係があるとき、
という関係があるとき、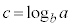 と書いて、cは、bを底とするaの対数であると言う。
と書いて、cは、bを底とするaの対数であると言う。
このとき、aを対数の真数と言う。
対数の真数は正数(この条件を真数条件と言います)、底は1以外の正数である。
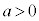 ,
,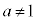 ,
,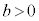 ,
,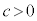 として、対数には、以下の性質がある。
として、対数には、以下の性質がある。
1) 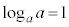
2) 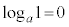
3) 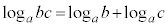
4) 
5) 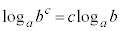
上記の対数の性質を証明しておきましょう。
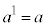 ⇔
⇔ 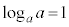
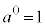 ⇔
⇔ 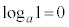
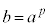 ,
,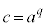 として、
として、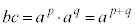 ⇔
⇔ 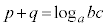
∴ 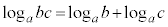
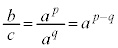 ⇔
⇔ 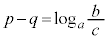
∴ 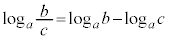
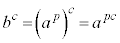 ⇔
⇔ 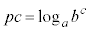
∴ 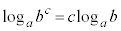 (証明終)
(証明終)
底の変換公式: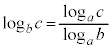
[証明] 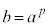 ,
,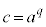 として、
として、
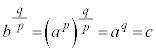 ⇔
⇔ 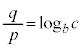
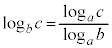
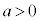 ,
,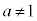 のとき、正数xに対して、実数yを、
のとき、正数xに対して、実数yを、 で決めるとき、
で決めるとき、 をaを底とする対数関数と言う。
をaを底とする対数関数と言う。
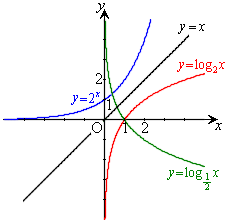
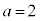 の場合と
の場合と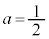 の場合について、
の場合について、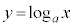 のグラフを右に示します。
のグラフを右に示します。
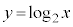 のグラフは、単調増加で、
のグラフは、単調増加で、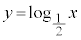 のグラフは、単調減少です。
のグラフは、単調減少です。
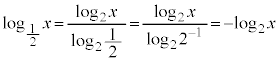 より、
より、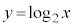 のグラフと
のグラフと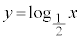 のグラフとは、x軸に関して対称です。
のグラフとは、x軸に関して対称です。
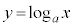 のグラフは、
のグラフは、 より、aの値にかかわらず、点
より、aの値にかかわらず、点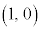 を通ります。
を通ります。
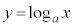 ⇔
⇔ 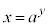 より、対数関数:
より、対数関数: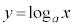 は、指数関数:
は、指数関数: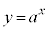 の逆関数です。
の逆関数です。
従って、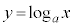 のグラフは、
のグラフは、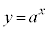 のグラフと、直線:
のグラフと、直線: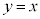 に関して対称です。
に関して対称です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 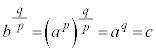 ⇔
⇔ 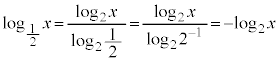 より、
より、