外積 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
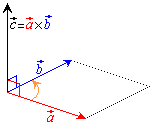 空間内に2個のベクトル
空間内に2個のベクトル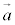 ,
,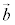 があって、
があって、
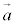 ,
,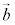 が1次独立でないときには、
が1次独立でないときには、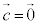 ,
,
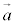 ,
,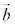 が1次独立なときには、
が1次独立なときには、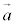 の向きから
の向きから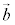 の向きまで回る向きを右ねじの回る向きとして、右ねじの進む向きをベクトルの向きとし、
の向きまで回る向きを右ねじの回る向きとして、右ねじの進む向きをベクトルの向きとし、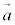 と
と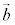 とで張られる平行四辺形の面積をベクトルの大きさとするようなベクトルを、
とで張られる平行四辺形の面積をベクトルの大きさとするようなベクトルを、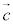
とするとき、この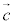 を
を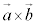 と書いて、
と書いて、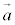 ,
,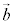 の外積と言う。
の外積と言う。
注.内積をスカラー積、外積をベクトル積と言うこともあります。
右ねじが進む向きは、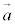 の向き、
の向き、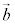 の向きのいずれとも垂直です。
の向きのいずれとも垂直です。
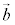 から
から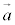 まで回る右ねじが進む向きは、
まで回る右ねじが進む向きは、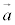 から
から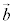 まで回る右ねじと進む向きが逆になるので、
まで回る右ねじと進む向きが逆になるので、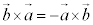 です。
です。
また、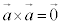 です。
です。
(1) 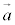 と
と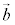 がともにxy平面内のベクトルで、
がともにxy平面内のベクトルで、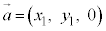 ,
,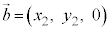 であるとき、
であるとき、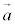 と
と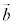 とで作る三角形の面積は、
とで作る三角形の面積は、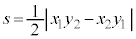 で与えられるので、
で与えられるので、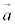 と
と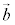 とで張られる平行四辺形の面積は、
とで張られる平行四辺形の面積は、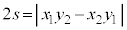 です。
です。 従って、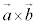 は、大きさが
は、大きさが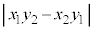 でz軸と平行なベクトルです。
でz軸と平行なベクトルです。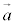 から
から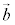 へと回る向きが、z軸正方向から見て反時計回りのときにはz軸正方向、時計回りのときにはz軸負方向になり、
へと回る向きが、z軸正方向から見て反時計回りのときにはz軸正方向、時計回りのときにはz軸負方向になり、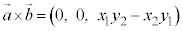 となります。
となります。
注.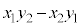 は、
は、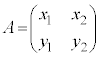 という行列の行列式
という行列の行列式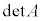
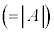 なので、
なので、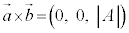 と書くことができます。
と書くことができます。
(2) 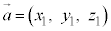 ,
,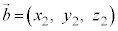 であるとき、
であるとき、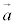 と
と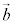 との外積は、行列式を用いて、
との外積は、行列式を用いて、 です。高校の範囲外ですが、これを暗記しておくと大学受験でも何かと便利です。(1)は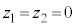 の場合に当たります。
の場合に当たります。
この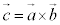 が上記の外積の定義を満たしていることを確かめておきます。
が上記の外積の定義を満たしていることを確かめておきます。 ∴ 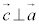
同様に、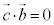 で、
で、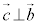
また、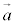 と
と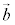 とで張られる平行四辺形の面積Sは、
とで張られる平行四辺形の面積Sは、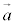 と
と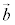 とで作る三角形の面積の2倍で、
とで作る三角形の面積の2倍で、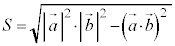
∴ 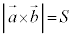
さてここで、(1)からわかるように、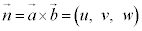 として、
として、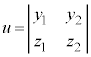 ,
,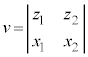 ,
,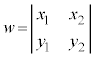 は、それぞれ、
は、それぞれ、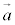 と
と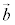 とで張られる平行四辺形に、x軸,y軸,z軸に平行に光を当てたときに、yz平面,zx平面,xy平面にできる影の面積に符号をつけたものです。この平行四辺形を含む平面πに垂直なベクトル(法線ベクトル)
とで張られる平行四辺形に、x軸,y軸,z軸に平行に光を当てたときに、yz平面,zx平面,xy平面にできる影の面積に符号をつけたものです。この平行四辺形を含む平面πに垂直なベクトル(法線ベクトル)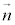 とx軸,y軸,z軸となす角をα,β,γとすると、
とx軸,y軸,z軸となす角をα,β,γとすると、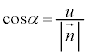 ,
,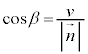 ,
,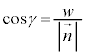 より、
より、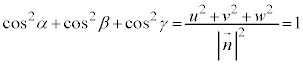 (これは、
(これは、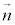 が外積だから言えることではなく、
が外積だから言えることではなく、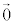 でないすべてのベクトルについて言えることです。
でないすべてのベクトルについて言えることです。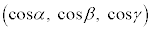 を方向余弦と言います)また、平面πの法線ベクトルとyz平面,zx平面,xy平面がなす角は、α,β,γなので、平行四辺形の面積をSとして、
を方向余弦と言います)また、平面πの法線ベクトルとyz平面,zx平面,xy平面がなす角は、α,β,γなので、平行四辺形の面積をSとして、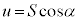 ,
,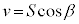 ,
,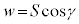
これより、 ∴ 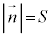
例1.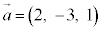 ,
,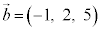 の双方に垂直なベクトルを1つ求める。
の双方に垂直なベクトルを1つ求める。
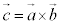
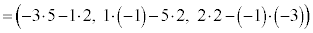
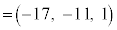
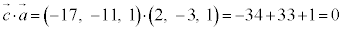
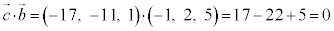
∴ 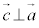 ,
,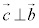
よって、求めるベクトルは、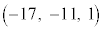 ......[答]
......[答]
注.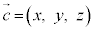 とおいて、
とおいて、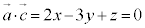 ,
,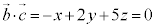 を連立しても同様の結果が得られます。
を連立しても同様の結果が得られます。
例2.3点A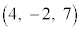 ,B
,B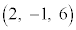 ,C
,C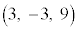 を頂点とする三角形の面積を求める。
を頂点とする三角形の面積を求める。
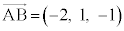 ,
,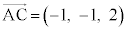
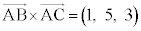
よって、求める三角形の面積は、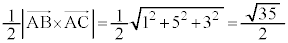 ......[答]
......[答]
注.公式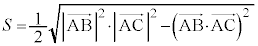 によっても、
によっても、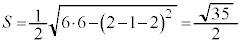 となります。
となります。
以上のように、外積は、大学入試においても、2つの空間ベクトルの双方に垂直なベクトルを求めたり、2つの空間ベクトルで張られる平行四辺形の面積、よって、三角形の面積を求めるときに有効な手段です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 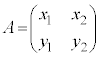 という行列の行列式
という行列の行列式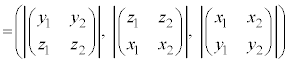
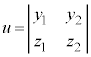 ,
,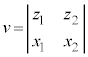 ,
,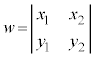 は、それぞれ、
は、それぞれ、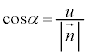 ,
,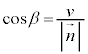 ,
,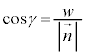 より、
より、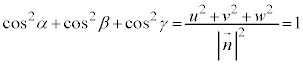 (これは、
(これは、