三角関数を含む方程式・不等式 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目の内容については、三角関数も参照してください。この項目では、三角関数を含む関数の増減を調べるときなどに出てくる三角関数を含む方程式・不等式の基本形を調べます。
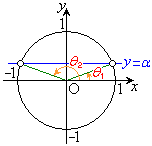 (i)
(i) 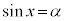 (
(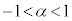 )
)
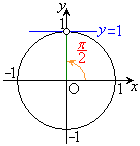
右図のように単位円を描いて、x軸に平行な直線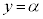 との交点を求め、原点とこの交点を直線で結んで、この直線までx軸から反時計回りに回った角を求めます。
との交点を求め、原点とこの交点を直線で結んで、この直線までx軸から反時計回りに回った角を求めます。
・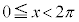 の場合、交点は2つできるので、解は、
の場合、交点は2つできるので、解は、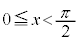 または
または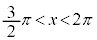 の範囲に1個(
の範囲に1個(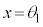 とします)、
とします)、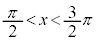 の範囲に1個(
の範囲に1個(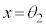 とします)、合わせて2個あります。
とします)、合わせて2個あります。
・xが全実数の場合の解は、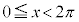 の範囲の解
の範囲の解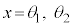 を用いて、
を用いて、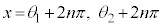 (nは整数)となります。
(nは整数)となります。
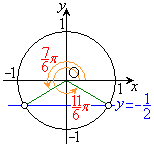 例1.(1)
例1.(1) 
・ の場合、
の場合、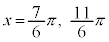
・xが全実数の場合の解は、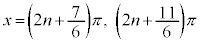 (nは整数)
(nは整数)
 (2)
(2) 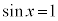
・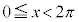 の場合、
の場合、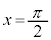
・xが全実数の場合の解は、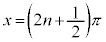 (nは整数)
(nは整数)
 (ii)
(ii) 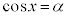 (
(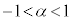 )
)
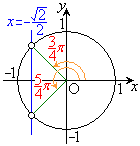
右図のように単位円を描いて、x軸に垂直な直線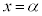 との交点を求め、原点とこの交点を直線で結んで、この直線までx軸から反時計回りに回った角を求めます。
との交点を求め、原点とこの交点を直線で結んで、この直線までx軸から反時計回りに回った角を求めます。
・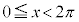 の場合、交点は2つできるので、解は、
の場合、交点は2つできるので、解は、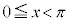 の範囲に1個(
の範囲に1個(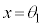 とします)、
とします)、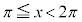 の範囲に1個(
の範囲に1個(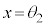 とします)、合わせて2個あります。
とします)、合わせて2個あります。
・xが全実数の場合の解は、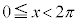 の範囲の解
の範囲の解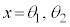 を用いて、
を用いて、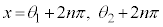 (nは整数)となります。
(nは整数)となります。
 例2.(1)
例2.(1) 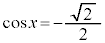
・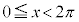 の場合、
の場合、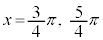
・xが全実数の場合の解は、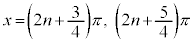 (nは整数)
(nは整数)
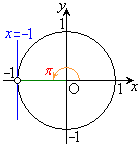 (2)
(2) 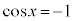
・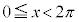 の場合、
の場合、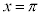
・xが全実数の場合の解は、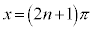 (nは整数)
(nは整数)
 (iii)
(iii) 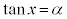
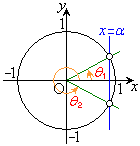
右図のように単位円を描いて右端で円に接する接線を引き、接線上でy座標がαの点と円の中心を直線で結び、x軸から反時計回りに回った角を求めます。
・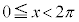 の場合、交点は2つあるので、解は、
の場合、交点は2つあるので、解は、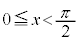 または
または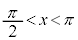 の範囲に1個(
の範囲に1個(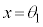 とします)、
とします)、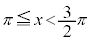 または
または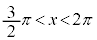 の範囲に1個(
の範囲に1個(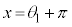 になります)、合わせて2個あります。
になります)、合わせて2個あります。
・xが全実数の場合の解は、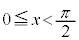 または
または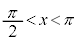 の範囲の解
の範囲の解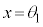 を用いて、
を用いて、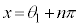 (nは整数)となります。
(nは整数)となります。
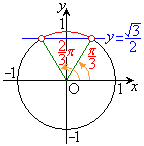
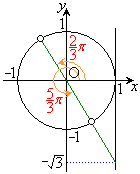 例3.
例3.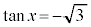
・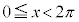 の場合、
の場合、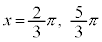
・xが全実数の場合の解は、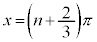 (nは整数)
(nは整数)
 例4.(1)
例4.(1) 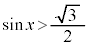
・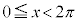 の場合、
の場合、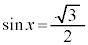 を満たすxは、
を満たすxは、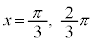 ,
,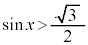 を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、
を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、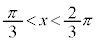
・xが全実数の場合の解は、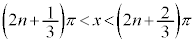 (nは整数)
(nは整数)
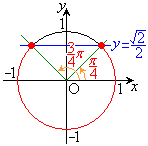 (2)
(2) 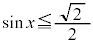
・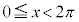 の場合、
の場合、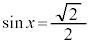 を満たすxは、
を満たすxは、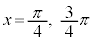 ,
,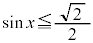 を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、
を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、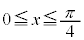 ,
,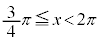
・xが全実数の場合の解は、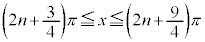 (nは整数)
(nは整数)
注.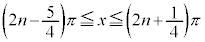 という解答でも同じです。
という解答でも同じです。
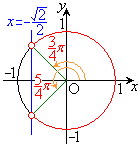 例5.(1)
例5.(1) 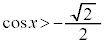
・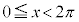 の場合、
の場合、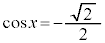 を満たすxは、
を満たすxは、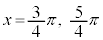 ,
,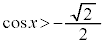 を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、
を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、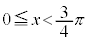 ,
,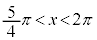
・xが全実数の場合の解は、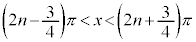 (nは整数)
(nは整数)
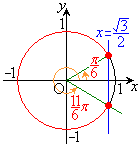 (2)
(2) 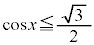
・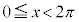 の場合、
の場合、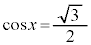 を満たすxは、
を満たすxは、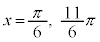 ,
,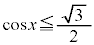 を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、
を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、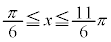
・xが全実数の場合の解は、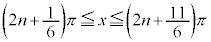 (nは整数)
(nは整数)
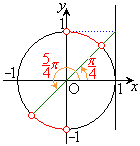 例6.(1)
例6.(1) 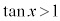
・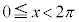 の場合、
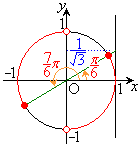
の場合、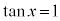 を満たすxは、
を満たすxは、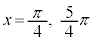 ,
,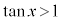 を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、
を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、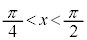 ,
,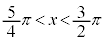
・xが全実数の場合の解は、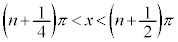 (nは整数)
(nは整数)
 (2)
(2) 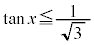
・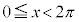 の場合、
の場合、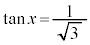 を満たすxは、
を満たすxは、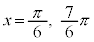 ,
,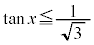 を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、
を満たすのは、右図の赤い部分の範囲と円の中心を結んでできる角で、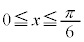 ,
,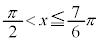 ,
,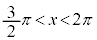
・xが全実数の場合の解は、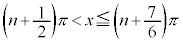 (nは整数)
(nは整数)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。