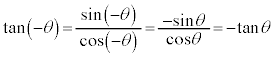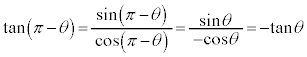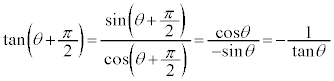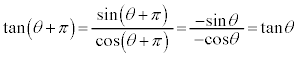三角関数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
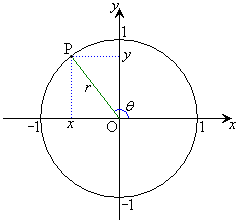 右図の、原点Oを中心とする半径rの円周上の点P
右図の、原点Oを中心とする半径rの円周上の点P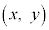 に対して、角θ はx軸から反時計回りに線分OPまで回転した角とする(時計回りに回るときには負の値とする)。
に対して、角θ はx軸から反時計回りに線分OPまで回転した角とする(時計回りに回るときには負の値とする)。
ここで、θ は、全実数をとりうるものとして、角θ は一般角で三角比を考えます。n周すると円周上の同じところに戻ってくるので、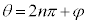 (
(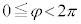 )として、
)として、
とします。
従って、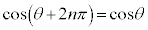 , ,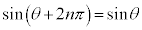 (nは整数) (nは整数) |
が成り立ちます。
こうして、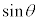 ,
,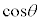 を、全ての実数で定義された関数として考えることができます。
を、全ての実数で定義された関数として考えることができます。
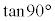 (
(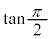 ),
),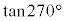 (
(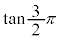 )が定義できないので、nを整数として、
)が定義できないので、nを整数として、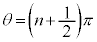 においては、
においては、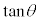 は定義できませんが、
は定義できませんが、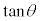 を、
を、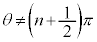 において定義される関数と考えることができます。
において定義される関数と考えることができます。
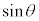 ,
,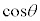 ,
,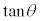 を総称して三角関数と言います。
を総称して三角関数と言います。
三角関数の値については(三角比の拡張を参照)、
などとなっています。
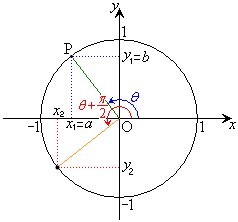
 右図の図1で、座標
右図の図1で、座標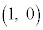 の点をAとします。単位円(原点を中心とする半径1の円)の円周上の点P
の点をAとします。単位円(原点を中心とする半径1の円)の円周上の点P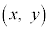 の座標は、
の座標は、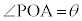 とするとき、
とするとき、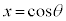 ,
,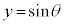 となります。また、直線OPと直線:
となります。また、直線OPと直線: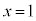 (点Aでx軸と直交する直線)との交点をQとすると、
(点Aでx軸と直交する直線)との交点をQとすると、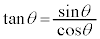 はQのy座標です。
はQのy座標です。
注.つまり、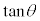 は直線OPの傾きです。一般に、直線:
は直線OPの傾きです。一般に、直線: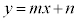 とx軸正方向との間の角をθとして、
とx軸正方向との間の角をθとして、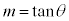 です。
です。
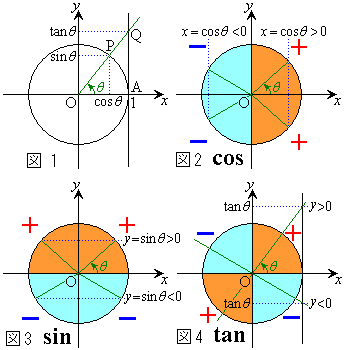
円周上の点のx座標,y座標の正負を考えることにより、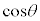 ,
,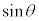 ,
,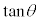 の符号は、第1象限、第2象限、第3象限、第4象限で右図の図2,図3,図4のようになります。
の符号は、第1象限、第2象限、第3象限、第4象限で右図の図2,図3,図4のようになります。
また、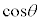 ,
,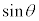 は円周上の点Pのx座標,y座標なので、最大値は1,最小値は
は円周上の点Pのx座標,y座標なので、最大値は1,最小値は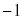 です。
です。
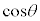 ,
,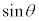 は
は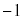 から1までの全ての実数をとります。
から1までの全ての実数をとります。
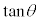 は、θ が0から
は、θ が0から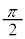 まで変化すると、どんどん大きな値になって行きます。
まで変化すると、どんどん大きな値になって行きます。
θ が0から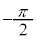 まで変化すると、どんどん小さな値(負の値で、絶対値はどんどん大きくなる)になって行きます。
まで変化すると、どんどん小さな値(負の値で、絶対値はどんどん大きくなる)になって行きます。
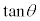 はすべての実数の値をとります。
はすべての実数の値をとります。
円はx軸に関して対称なので、単位円の円周に沿って、点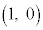 から角θ 回った位置のx座標と、角
から角θ 回った位置のx座標と、角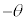 回った位置のx座標は同じです。よって、
回った位置のx座標は同じです。よって、
これは、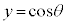 という関数が偶関数(グラフがy軸に関して対称)であることを意味しています。
という関数が偶関数(グラフがy軸に関して対称)であることを意味しています。
また、単位円の円周に沿って、点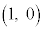 から角θ 回った位置のy座標と、角
から角θ 回った位置のy座標と、角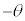 回った位置のy座標は、絶対値が等しく符号が逆です。よって、
回った位置のy座標は、絶対値が等しく符号が逆です。よって、
これは、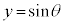 という関数が奇関数(グラフが原点に関して対称)であることを意味しています。
という関数が奇関数(グラフが原点に関して対称)であることを意味しています。
より、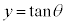 という関数は奇関数です。
という関数は奇関数です。
これらより、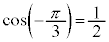 ,
,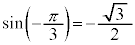 ,
,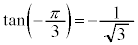 などとなります。
などとなります。
円はy軸に関して対称なので、単位円の円周に沿って、点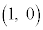 から角θ 回った位置のx座標と、点
から角θ 回った位置のx座標と、点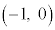 から角
から角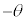 回った位置、つまり点
回った位置、つまり点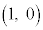 から
から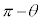 回った位置のx座標は、絶対値が等しく符号が逆です。よって、
回った位置のx座標は、絶対値が等しく符号が逆です。よって、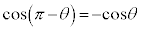
また、単位円の円周に沿って、点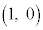 から角θ 回った位置のy座標と、点
から角θ 回った位置のy座標と、点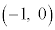 から角
から角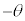 回った位置のy座標は同じです。よって、
回った位置のy座標は同じです。よって、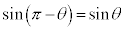
 右図のように、単位円の円周に沿って、点
右図のように、単位円の円周に沿って、点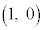 から角θ 回った点
から角θ 回った点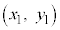 と、角
と、角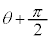 回った点
回った点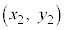 の座標を比べると、
の座標を比べると、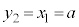 ,
,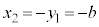 という関係があります。
という関係があります。
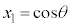 ,
,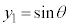 ,
,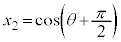 ,
,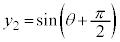 より、
より、
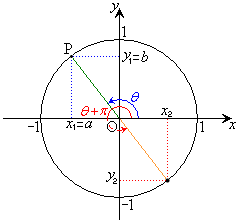 右図のように、単位円の円周に沿って、点
右図のように、単位円の円周に沿って、点 から角θ 回った点
から角θ 回った点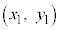 と、角
と、角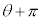 回った点
回った点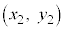 の座標を比べると、
の座標を比べると、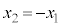 ,
,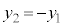 という関係があります。
という関係があります。
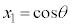 ,
,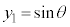 ,
,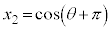 ,
,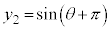 より、
より、
三角比の拡張で取り上げた公式も含め、以上をまとめると、
類似の公式がいくつも作れますが、混乱の元になるので、覚えるのは上記のものだけにすること。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。