東大理系数学'01年前期[1]
半径rの球面上に4点A，B，C，Dがある。四面体ABCDの各辺の長さは、
，
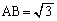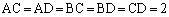
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 文理共通の問題で、本当は中学生でも解答可能な易しい空間図形の問題なのですが、第1問に来ているので、気負って取り組み、空間座標を設定し出したりするとハマってしまうかも知れません。ベクトルの内積計算を利用するのも、かえって煩雑になります。
空間図形の入試問題は、真に空間的な思考力を必要とする難問もありますが、ほとんどの問題は、本問のように、対称性や切断面をうまく考えて解決できます。
本問では、四面体はABの中点とC，Dを通る平面に関して対称なので、この面で切った断面の二等辺三角形がどうなるかというところから考えればよいのです。
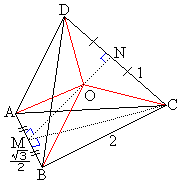右図のような図が描けてさえしまえば、三平方の定理のみで解決できてしまいます。
半径rの球面の中心をOとして、球面上に4点A，B，C，Dがあるので、
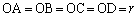(右図赤線)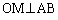
三角形OBMにおいて、三平方の定理より、
また、三角形ABCと三角形ABDは3辺が等しく合同です。従って、
三角形CDMは二等辺三角形です。これより、CDの中点をNとして、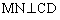
三角形OCNに三平方の定理を適用すると、
また、三角形CMBに三平方の定理を適用すると、
三角形CMNに三平方の定理を適用すると、
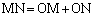より、
2乗して、
2乗して、
∴ 
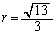......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
