東大理系数学'03年前期[6]
円周率が3.05より大きいことを証明せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 いろいろ考えられますが、円に内接する正多角形の周の長さを考えるのがやはり一番簡単です。
，
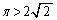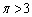を示しただけでは、
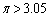を示したことにはならないので注意。
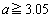だとして、
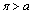を示さなければなりません。なお、条件・命題を参照してください。
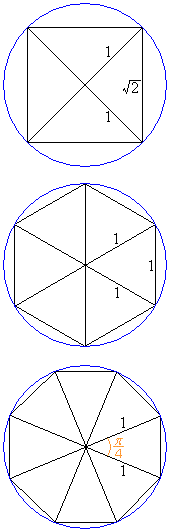
まず、半径1の円に内接する正方形を考えてみます。
半径1の円の円周の長さは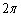
です。
半径1の円に内接する正方形の1辺の長さは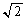
です。正方形の周の長さは4辺で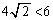
円周の長さは、円に内接する正方形の周の長さよりも長いので、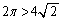
ですが、これでは、
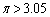が示せません。
次に、半径1の円に内接する正六角形を考えてみます。
この正六角形の1辺の長さは1です。正六角形の周の長さは6辺で6
円周の長さは、円に内接する正六角形の週の長さよりも長いので、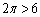
ですが、これでも、
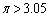は示せません。
今度は、半径1の円に内接する正八角形を考えてみます。
この正八角形の1辺の長さは、中心からこの1辺に垂線を下ろすと垂線の足はこの1辺の中点なので、
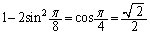より、
(
)
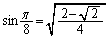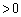円周の長さは、円に内接する正八角形の周の長さより長いので、
というわけで、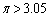
を言うためには、
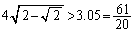，つまり、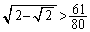
が言えればよいわけです。
2乗すると、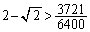
，移項して、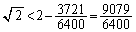
さらに2乗して、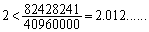
答案としては、
半径1の円周は、この円に内接する正八角形の周の長さ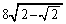
より長いから、
ところで、
∴ 
∴ 
∴ 
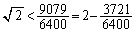
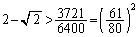
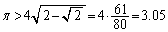
のようにまとめればよいでしょう。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
