東大文系数学'07年前期[3]

東大文系数学'07年前期[3]

正の整数の下2桁とは、100の位以上を無視した数をいう。たとえば2000，12345の下2桁はそれぞれ0，45である。mが正の整数全体を動くとき、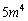

の下2桁として現れる数をすべて求めよ。

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

解答　mを10で割った余りで分類して考えます(整数を参照)。

mを10で割り、商をk，余りをjとします。jは、0，1，2，･･･，9のどれかです。

従って、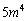

と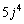

の下2桁は一致します。つまり、正の整数mに対して

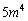の下2桁を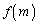

，正の整数nの下2桁を

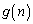として、

これを用いて、

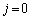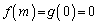
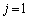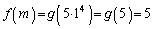
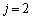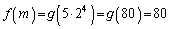
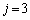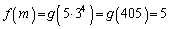
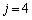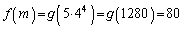
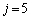のとき、

のとき、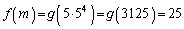

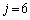のとき、

のとき、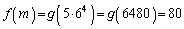

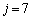のとき、

のとき、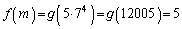

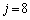のとき、

のとき、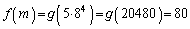

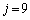のとき、

のとき、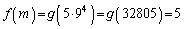

これですべての場合を尽くしました。

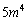の下2桁として現れる数は、0，5，25，80 ......[答]

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

　　数学TOP　　TOPページに戻る

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。

【広告】広告はここまでです。

各問題の著作権は
出題大学に属します。
©2005-2024
(有)りるらる

苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。