東大文系数学'08年前期[2]
白黒2種類のカードがたくさんある。そのうち4枚を手もとに持っているとき、次の操作(A)を考える。
(A) 手持ちの4枚の中から1枚を、等確率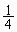 で選び出し、それを違う色のカードにとりかえる。
で選び出し、それを違う色のカードにとりかえる。 最初に持っている4枚のカードは、白黒それぞれ2枚であったとする。以下の(1),(2)に答えよ。
(1) 操作(A)を4回繰り返した後に初めて、4枚とも同じ色のカードになる確率を求めよ。
(2) 操作(A)をn回繰り返した後に初めて、4枚とも同じ色のカードになる確率を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 理系前期[2]の(1)の部分を1題にした問題です。ケアレスや勘違いのないように慎重に考えましょう。理系前期[2]も参考にしてください。
(1) 1回目に白を引く(白は4枚中2枚あるので、確率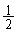 )と、白が黒に変わって、白1枚、黒3枚となり、さらに2回目に白を引く(白は4枚中1枚あるので、確率
)と、白が黒に変わって、白1枚、黒3枚となり、さらに2回目に白を引く(白は4枚中1枚あるので、確率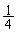 )と全て黒になります。この確率は、
)と全て黒になります。この確率は、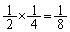 (独立試行の確率を参照)
(独立試行の確率を参照) このとき、2回目に黒を引く(黒は4枚中3枚あるので、確率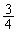 )と、元の状態に戻ってしまいます。この確率は、
)と、元の状態に戻ってしまいます。この確率は、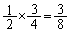
白と黒が逆になった場合も同じで、2回の操作で、4枚とも同じ色になる確率は、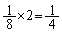 2回の操作で元の状態に戻る確率が、
2回の操作で元の状態に戻る確率が、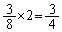
「初めて、4枚とも同じ色のカードになる確率」を聞いているので、2回の操作で4枚とも同じ色になってしまった以降を考える必要はありません。3回目の操作と4回目の操作では、1回目、2回目のときと同じことが起こります。つまり、3回目、4回目の2回の操作で、4枚とも同じ色になる確率は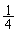 ,元に戻る確率は
,元に戻る確率は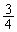 です。1回目、2回目の操作で元に戻ってしまう状況下で、3回目、4回目を考えるので、1回目、2回目、と、3回目、4回目、における結果は独立に起こります。
です。1回目、2回目の操作で元に戻ってしまう状況下で、3回目、4回目を考えるので、1回目、2回目、と、3回目、4回目、における結果は独立に起こります。
従って、1回目、2回目で元に戻り、3回目、4回目で4枚とも同じ色になる確率として、求める確率は、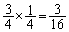 ......[答]
......[答]
(2) この後、同様のことが繰り返されて、mを自然数として、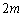 回操作を行うと、4枚とも同じ色になるか、元の状態に戻ります。一度、4枚とも同じ色になってしまうと、それ以降は考える必要はありません。
回操作を行うと、4枚とも同じ色になるか、元の状態に戻ります。一度、4枚とも同じ色になってしまうと、それ以降は考える必要はありません。 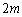 回の操作で元の状態に戻る確率は、
回の操作で元の状態に戻る確率は、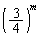
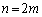 回の操作で4枚とも同じ色になる確率は、
回の操作で4枚とも同じ色になる確率は、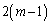 回目に元の状態で、その後の2回の操作で、同じ色を2回引いた場合です。その確率は、
回目に元の状態で、その後の2回の操作で、同じ色を2回引いた場合です。その確率は、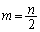 より、
より、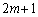 回目には、片方が3枚で、他方が1枚となり、4枚とも同じ色になることはありません。
回目には、片方が3枚で、他方が1枚となり、4枚とも同じ色になることはありません。
よって、n回の操作で、4枚とも同じ色になる確率は、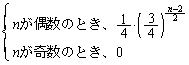 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 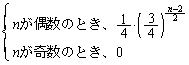 ......[答]
......[答]