���嗝�n���w'08�N�O��[2]
����2��ނ̃J�[�h����������B���̂���k���̃J�[�h������Ƃɂ����Ă���Ƃ��A���̑���(A)���l����B
(A)�@�莝����k���̒�����1�����A���m��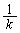 �őI�яo���A������Ⴄ�F�̃J�[�h�ɂƂ肩����B
�őI�яo���A������Ⴄ�F�̃J�[�h�ɂƂ肩����B �ȉ��̖�(1)�C(2)�ɓ�����B
(1) �ŏ��ɔ�2���A��2���A���v4���̃J�[�h�������Ă���Ƃ��A����(A)��n��J��Ԃ�����ɏ��߂āA4���Ƃ������F�̃J�[�h�ɂȂ�m�������߂�B
(2) �ŏ��ɔ�3���A��3���A���v6���̃J�[�h�������Ă���Ƃ��A����(A)��n��J��Ԃ�����ɏ��߂āA6���Ƃ������F�̃J�[�h�ɂȂ�m�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����́A��r�I�A�m���͎��g�݈Ղ���肪�����C�����܂��B�����_�A�P�A���X�A�ꍇ�����̘R��A�Ȃǂɒ��ӂ��Ă��������B
(1)�C(2)�Ƃ��A�������t�ɂȂ��Ă��ς�肪�Ȃ��Ƃ�������܂��l���܂��傤�B�܂��A�u���߂āv�����F�ɂȂ�m�������߂�̂ŁA��x�A�����F�ɂȂ��Ă��܂����ꍇ�́A����ȍ~�͍l����K�v���Ȃ����Ƃɂ����ӂ��Ă��������B
(1) 1��ڂɔ�������(�m��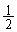 )�ƁA�������ɕς���āA��1���A��3���ƂȂ�A�����2��ڂɔ�������(�m��
)�ƁA�������ɕς���āA��1���A��3���ƂȂ�A�����2��ڂɔ�������(�m��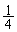 )�ƑS�č��ɂȂ�܂��B���̊m���́A
)�ƑS�č��ɂȂ�܂��B���̊m���́A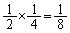 �@(�Ɨ����s�̊m�����Q��)
�@(�Ɨ����s�̊m�����Q��) ���̂Ƃ��A2��ڂɍ�������(�m��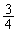 )�ƁA���̏�Ԃɖ߂��Ă��܂��܂��B���̊m���́A
)�ƁA���̏�Ԃɖ߂��Ă��܂��܂��B���̊m���́A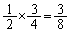
���ƍ����t�ɂȂ����ꍇ�������ŁA2��̑���ŁA4���Ƃ������F�ɂȂ�m���́A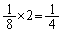 2��̑���Ō��̏�Ԃɖ߂�m�����A
2��̑���Ō��̏�Ԃɖ߂�m�����A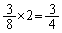
���̌�A���l�̂��Ƃ��J��Ԃ���āAm�����R���Ƃ��āA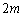 ����s���ƁA4���Ƃ������F�ɂȂ邩�A���̏�Ԃɖ߂�܂��B��x�A4���Ƃ������F�ɂȂ��Ă��܂��ƁA����ȍ~�͍l����K�v�͂���܂���B
����s���ƁA4���Ƃ������F�ɂȂ邩�A���̏�Ԃɖ߂�܂��B��x�A4���Ƃ������F�ɂȂ��Ă��܂��ƁA����ȍ~�͍l����K�v�͂���܂���B
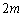 ��̑���Ō��̏�Ԃɖ߂�m���́A
��̑���Ō��̏�Ԃɖ߂�m���́A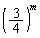
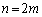 ��̑����4���Ƃ������F�ɂȂ�m���́A
��̑����4���Ƃ������F�ɂȂ�m���́A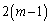 ��ڂɌ��̏�ԂŁA���̌��2��̑���ŁA�����F��2��������ꍇ�ł��B���̊m���́A
��ڂɌ��̏�ԂŁA���̌��2��̑���ŁA�����F��2��������ꍇ�ł��B���̊m���́A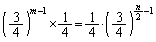
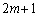 ��ڂɂ́A�Е���3���ŁA������1���ƂȂ�A4���Ƃ������F�ɂȂ邱�Ƃ͂���܂���B
��ڂɂ́A�Е���3���ŁA������1���ƂȂ�A4���Ƃ������F�ɂȂ邱�Ƃ͂���܂���B
����āAn��̑���ŁA4���Ƃ������F�ɂȂ�m���́A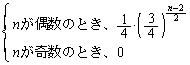 ......[��]
......[��]
(2) 1��ڂɔ��������ƁA����2���A����4���ƂȂ�A2��ڂɔ��������ƁA����1���A����5���ƂȂ�A3��ڂɔ��������ƁA6���Ƃ����ɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 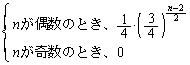 ......[��]
......[��] ......[��]
......[��]