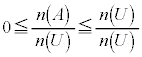積事象・和事象・余事象 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
2つの事象Aと事象Bが起こるときに、
事象Aと事象Bがともに起こるという事象を積事象と言います。事象を集合で表すと、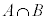 に相当します。
に相当します。
事象Aまたは事象Bが起こる事象を和事象と言います。事象を集合で表すと、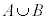 に相当します。
に相当します。
「事象Aと事象Bが同時に起こること」がないとき、つまり、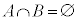 のとき、事象Aと事象Bは、排反であると言います。
のとき、事象Aと事象Bは、排反であると言います。
集合の公式(集合の要素の数を参照):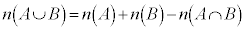
の両辺を、全事象の場合の数: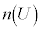 で割ると、
で割ると、
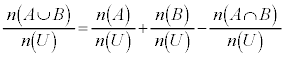
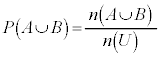 ,
,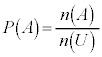 ,
,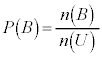 ,
,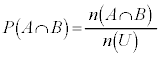 として(確率を参照)、
として(確率を参照)、
和事象の確率の公式: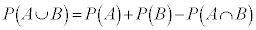
が得られます。
ここで、特に、事象Aと事象Bが排反であるとき、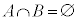 より、
より、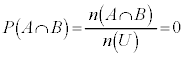 となり、
となり、
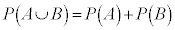
となります。これを確率の加法定理と言います。
3つ以上の事象についても、全く同様です。互いに排反な事象A,B,Cの和事象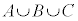 の確率は、それぞれの事象が起こる確率の和です。つまり、
の確率は、それぞれの事象が起こる確率の和です。つまり、
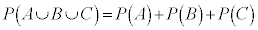
例1.1から30までの数が書かれたカードが1枚ずつ30枚ある。この中から1枚を無作為に選んだときに、5の倍数と7の倍数の書かれたカードを選ぶ確率を求めよ。
[解答] 1から30までの数の中には5の倍数であってかつ7の倍数である数は存在しないので、5の倍数を選ぶ事象と7の倍数を選ぶ事象は排反です。
5の倍数は6通りで、5の倍数を選ぶ確率は、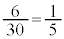
7の倍数は4通りで、7の倍数を選ぶ確率は、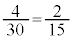
求める確率は、両者の和となり、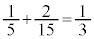 ......[答]
......[答]
ここで、1から60までのカードだと、5の倍数は12通り、7の倍数は8通り、35の倍数が1通りで、確率は、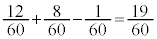 となります。
となります。
全事象Uに対して、「事象Aが起こらない」という事象を事象Aの余事象と言います。
集合の公式(集合の要素の数を参照):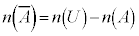
の両辺を、全事象の場合の数: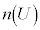 で割ると、
で割ると、
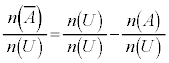
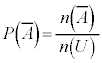 ,
,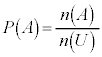 として、
として、
余事象の確率の公式: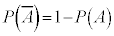
が得られます。
例2.サイコロを3個振るときに出た目の積が偶数になる確率を求めよ。
[解答] 3個の目の積が偶数となるのは、3個のうちどれか1個が偶数になればよいのですが、3個のうち2個が偶数の場合、3個とも偶数の場合の重複を考える必要があって面倒です。このように、場合分けが複雑になってしまうときに余事象を考えます。
出た目の積が偶数となる事象の余事象は、出た目の積が奇数という事象ですが、これは、3個の目が全て奇数のときにしか起こりません。
奇数が目が出る確率は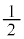 なので、3個とも奇数の目が出る確率は、
なので、3個とも奇数の目が出る確率は、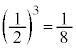 です。確率を考えている事象の余事象の確率が
です。確率を考えている事象の余事象の確率が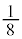 なので、元の事象の確率は、
なので、元の事象の確率は、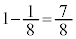 ......[答]
......[答]
なお、確率には重要な性質があります。
事象Aの確率を考えるときは、事象Aの場合の数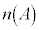 を全事象の場合の数
を全事象の場合の数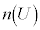 で割りますが、集合Aは全体集合Uの部分集合なので、
で割りますが、集合Aは全体集合Uの部分集合なので、
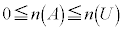 です。
です。
この各辺を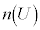 で割ると、
で割ると、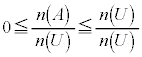
∴ 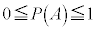
即ち、事象Aが起こる確率は、負の数になったり、1より大きい数にはなり得ません。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 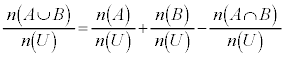
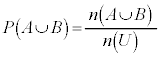 ,
,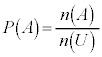 ,
,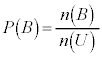 ,
,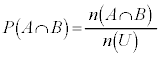 として(確率を参照)、
として(確率を参照)、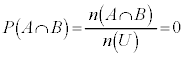 となり、
となり、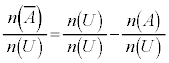
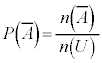 ,
,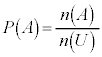 として、
として、