東京大学文系2010年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] Oを原点とする座標平面上に点A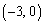
をとり、
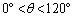の範囲にあるθ に対して、次の条件(i)，(ii)をみたす2点B，Cを考える。
(ii) Cは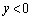
の部分にあり、
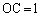かつ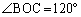
である。ただし、△ABCはOを含むものとする。 以下の問(1)，(2)に答えよ。
(1) △OABと△OACの面積が等しいとき、θ の値を求めよ。
(2) θ を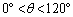
の範囲で動かすとき、△OABと△OACの面積の和の最大値と、そのときの
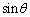の値を求めよ。 [解答へ]
[2] 2次関数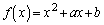
に対して
がxについて恒等式になるような定数a，b，cの組をすべて求めよ。
[解答へ]
[3] 2つの箱LとR，ボール30個、コイン投げで表と裏が等確率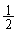
で出るコイン1枚を用意する。xを0以上30以下の整数とする。Lにx個，Rに
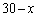個のボールを入れ、次の操作(＃)を繰り返す。
(＃) 箱Lに入っているボールの個数をzとする。コインを投げ、表が出れば箱Rから箱Lに、裏が出れば箱Lから箱Rに、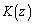
個のボールを移す。ただし、
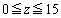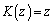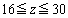のとき
，
のとき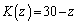
とする。
m回の操作の後、箱Lのボールの個数が30である確率を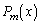
とする。たとえば
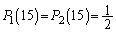となる。以下の問(1)，(2)，(3)に答えよ。
(1) 
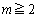のとき、xに対してうまくyを選び、
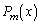を
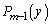で表せ。 (2) nを自然数とするとき、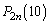
を求めよ。 [解答へ]
[4] Cを半径1の円周とし、AをC上の1点とする。3点P，Q，RがAを時刻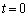
に出発し、C上を各々一定の速さで、P，Qは反時計回りに、Rは時計回りに、時刻
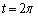まで動く。P，Q，Rの速さは、それぞれm，1，2であるとする。(したがって、QはCをちょうど一周する。)ただし、mは
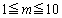をみたす整数である。△PQRがPRを斜辺とする直角二等辺三角形となるような速さmと時刻tの組をすべて求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
の部分にあり、
かつ
である。