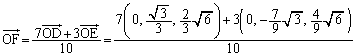東大文系数学'98年[4]
xyz空間に3点A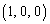 ,B
,B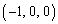 ,C
,C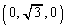 をとる。△ABCを1つの面とし、
をとる。△ABCを1つの面とし、 の部分に含まれる正四面体ABCDをとる。さらに△ABDを1つの面とし、点Cと異なる点Eをもう1つの頂点とする正四面体ABDEをとる。
の部分に含まれる正四面体ABCDをとる。さらに△ABDを1つの面とし、点Cと異なる点Eをもう1つの頂点とする正四面体ABDEをとる。
(1) 点Eの座標を求めよ。
(2) 正四面体ABDEの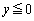 の部分の体積を求めよ。
の部分の体積を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 断面図が描けてしまえば、あとは一本道です。なお、空間ベクトルを参照してください。
 (1) 原点をOとして、Oは辺ABの中点で、
(1) 原点をOとして、Oは辺ABの中点で、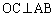 より、正四面体ABCDは、△CODを含む平面、つまり、yz平面に関して対称です。また、同様に、正四面体ABDEも、yz平面に関して対称です。従って、D,Eはyz平面上の点です。
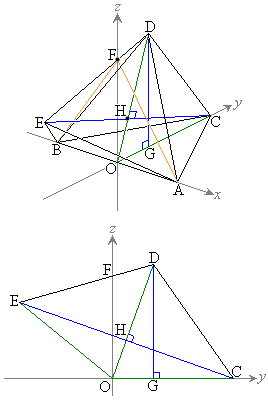
より、正四面体ABCDは、△CODを含む平面、つまり、yz平面に関して対称です。また、同様に、正四面体ABDEも、yz平面に関して対称です。従って、D,Eはyz平面上の点です。これより、右図のような鳥瞰図と、yz平面で切ったときの断面図が書けるはずです。
△ABCの重心をGとすると、断面図において、DGは△ABCを含む平面、つまり、xy平面に垂直 ・・・(*) で、Dのy座標はGのy座標に一致します。
よって、Dのy座標は です。また、
です。また、 と三平方の定理より、
と三平方の定理より、 これがDのz座標になります。
∴ 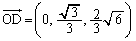
ODとCEの交点をHとすると、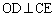 であって、Hは△ABDの重心です。
であって、Hは△ABDの重心です。
∴ 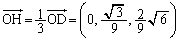
Eは直線OD (あるいは△ABD)に関してCと対称なので、 よって、点Eの座標は、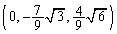 ......[答]
......[答] 注.(*)を示すのであれば、
よって、DGは△ABCを含む平面に垂直です。
(2) これも(1)の断面図を使って考えます。正四面体ABDEをzx平面で切ると、辺DEとz軸との交点をFとして、切り口は△ABFです。この△ABFを底面と見ると、高さはEのy座標の符号を変えたもの となり、求める体積Vは、
となり、求める体積Vは、 で与えられます。Dのy座標を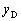 と書くと、GD // OFより、DF:FE =
と書くと、GD // OFより、DF:FE = 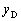 :
: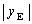 =
= 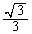 :
: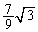 = 3:7∴
= 3:7∴ 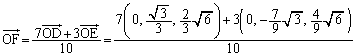
Fのz座標を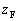 として、
として、 ∴  ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。