空間ベクトル 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
平面ベクトルにおいて、有向線分としてベクトルを定義しましたが、空間においても同様に、有向線分として空間ベクトルを定義します。
従って、平面ベクトルにおいて成り立つことは空間ベクトルにおいても、成分表示にz成分が付け加わるだけで、そのまま成り立ちます。
以下については、ベクトルとはを参照してください。
(1) 空間内に2点A,Bがあるとき、大きさが線分ABの長さであって、向きがAからBに向かう量を、ベクトル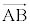 とする。
とする。 (2) 空間内に3点A,B,Cがあるとき、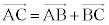
(4) 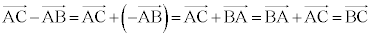
(5) 実数kについて、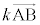 は、
は、 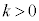 のとき、
のとき、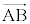 と同じ向きで長さがk倍となるベクトル
と同じ向きで長さがk倍となるベクトル
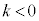 のとき、
のとき、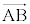 と正反対の向きで、長さが
と正反対の向きで、長さが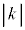 倍となるベクトル
倍となるベクトル
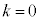 のとき、零ベクトル
のとき、零ベクトル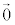
(6) ベクトルの和、差、実数倍は、文字の計算と同様に行う。
以下については、ベクトルの1次独立を参照してください。
(7) 空間内の2つのベクトル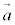 ,
,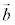 が平行 ⇔
が平行 ⇔ 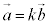 となる実数kがある。
となる実数kがある。 (8) 1次独立については、平面ベクトルと空間ベクトルで異なる点がある。
平面ベクトルでは、
平面上の2つのベクトル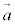 ,
,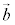 が1次独立
が1次独立
⇔ 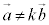 (k:実数) かつ
(k:実数) かつ 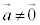 かつ
かつ 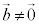
⇔ 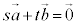 ならば
ならば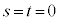
⇔ 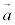 ,
,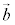 で三角形を作るような位置関係にある。
で三角形を作るような位置関係にある。
これが、空間ベクトルでは、
空間内の3つのベクトル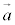 ,
,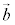 ,
,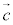 が1次独立
が1次独立
⇔ 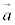 ,
,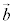 ,
,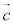 が零ベクトルでなく同一平面上に存在しない。
が零ベクトルでなく同一平面上に存在しない。
⇔ 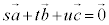 ならば
ならば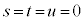
⇔ 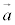 ,
,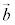 ,
,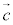 で四面体を作るような位置関係にある。
で四面体を作るような位置関係にある。
平面を2次元,空間を3次元と言うのは、平面ベクトルでは1次独立なベクトルの組が2個のベクトル、空間ベクトルでは1次独立なベクトルの組が3個のベクトルから成ることからきています。 (9) 1次結合の形も、平面ベクトルと空間ベクトルで異なる点がある。
平面ベクトルでは、1次独立な2つのベクトル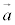 ,
,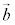 があるとき、平面内の任意のベクトル
があるとき、平面内の任意のベクトル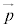 は、s,tを実数として、
は、s,tを実数として、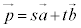 と表せる。また、実数s,tの組はただ1通りに定まる。
と表せる。また、実数s,tの組はただ1通りに定まる。
空間ベクトルでは、1次独立な3つのベクトル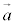 ,
,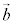 ,
,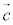 があるとき、空間内の任意のベクトル
があるとき、空間内の任意のベクトル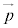 は、s,t,uを実数として、
は、s,t,uを実数として、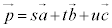 と表せる。また、実数s,t,uの組はただ1通りに定まる。
と表せる。また、実数s,t,uの組はただ1通りに定まる。
空間ベクトルでは、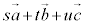 の形を1次結合と言う。
の形を1次結合と言う。 (10) 空間ベクトルでも、原点を始点とするベクトル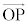 を、点Pの位置ベクトルと言う。
を、点Pの位置ベクトルと言う。
以下については、ベクトルの成分表示を参照してください。
(11) 空間ベクトルでも、大きさが1のベクトルを基本ベクトルと言う。
(12) 点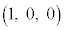 ,
,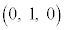 ,
,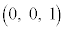 の位置ベクトルを
の位置ベクトルを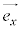 ,
,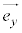 ,
,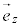 とすると、これらのベクトルは基本ベクトルであるとともに、1次独立である。空間内の任意の点P
とすると、これらのベクトルは基本ベクトルであるとともに、1次独立である。空間内の任意の点P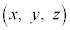 の位置ベクトル
の位置ベクトル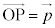 を、
を、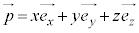 と表すことができる。x,y,zは点Pのx座標,y座標,z座標で、
と表すことができる。x,y,zは点Pのx座標,y座標,z座標で、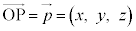 と表す。これを
と表す。これを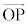 の成分表示と言い、x,y,zを
の成分表示と言い、x,y,zを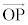 のx成分,y成分,z成分と言う。
のx成分,y成分,z成分と言う。 (13) 2つのベクトル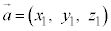 ,
,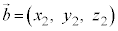 に対して、k,hを実数として、
に対して、k,hを実数として、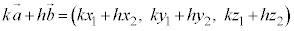
以下については、内積を参照してください。
(14) 2つのベクトル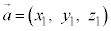 ,
,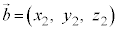 に対して、
に対して、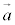 と
と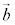 の内積
の内積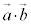 は、
は、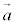 と
と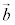 のなす角をθ として、
のなす角をθ として、 証明は、平面ベクトルにおける内積と同様に、三角形の余弦定理を用いればよい。 (15) 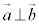 ⇔
⇔ 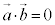
(16) 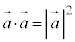
以下については、ベクトルの内分・外分を参照してください。
(17) 内分点、外分点の公式は、ベクトルとして書くときには、平面ベクトルと空間ベクトルとで同じ形をしています。
空間内の2点A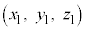 ,B
,B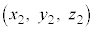 に対して、線分ABをm:nに内分する点Pの位置ベクトルは、
に対して、線分ABをm:nに内分する点Pの位置ベクトルは、 線分ABをm:nに外分する点Pの位置ベクトルは、
とくに、2点A,Bの中点は、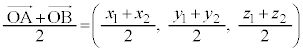
また、C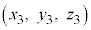 として、三角形ABCの重心は、
として、三角形ABCの重心は、
以下については、直線のベクトル方程式を参照してください。
(18) 直線のベクトル方程式は、ベクトルとして書くときには、平面ベクトルと空間ベクトルとで同じ形をしている。
空間内の点A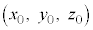 を通り、方向ベクトル:
を通り、方向ベクトル: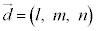 に平行な直線上の点Pの位置ベクトル
に平行な直線上の点Pの位置ベクトル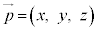 は、点Aの位置ベクトルを
は、点Aの位置ベクトルを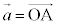 ,tを実数として、
,tを実数として、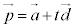
成分表示で書くと、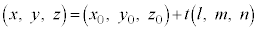
これより、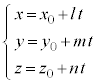 (これを直線の媒介変数表示と言う)媒介変数tを消去すると、
(これを直線の媒介変数表示と言う)媒介変数tを消去すると、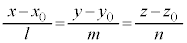 (
(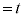 )これが空間図形における直線の方程式になる。
)これが空間図形における直線の方程式になる。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 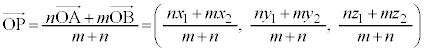
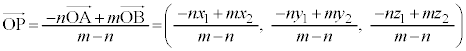
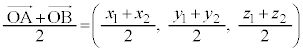
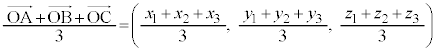
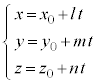 (これを直線の媒介変数表示と言う)
(これを直線の媒介変数表示と言う)