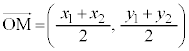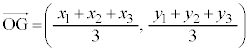ベクトルの内分・外分 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
 平面上の2点A
平面上の2点A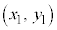 ,B
,B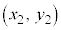 に対して、線分ABをm:nに内分する点Pの位置ベクトルは、
に対して、線分ABをm:nに内分する点Pの位置ベクトルは、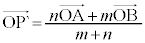
成分表示で書くと、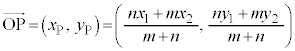 (図形と方程式で考えた内分点の座標と一致する。座標平面における内分・外分を参照)
(図形と方程式で考えた内分点の座標と一致する。座標平面における内分・外分を参照)
線分ABをm:nに外分する点のPの位置ベクトルは、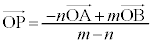
成分表示で書くと、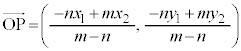 (図形と方程式で考えた外分の座標と一致する)
(図形と方程式で考えた外分の座標と一致する)
外分の公式は、内分の公式で、外分比の数値m,nのどちらかにマイナスをつけて、内分比と考えればOK。
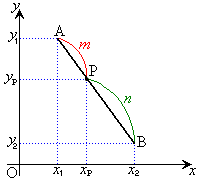
証明は、右上の図で、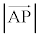 :
: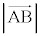 =
= 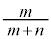 :1より、
:1より、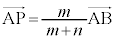
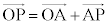
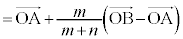
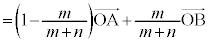
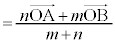
とくに、平面上の2点A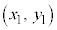 ,B
,B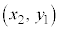 の中点Mの位置ベクトル
の中点Mの位置ベクトル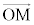 は、1:1に内分する点と考えれば、
は、1:1に内分する点と考えれば、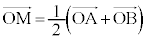
成分表示で書くと、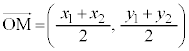
また、三角形の頂点がA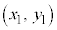 ,B
,B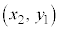 ,C
,C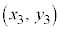 であるとき、三角形ABCの重心Gの位置ベクトルは、
であるとき、三角形ABCの重心Gの位置ベクトルは、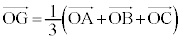
成分表示で書くと、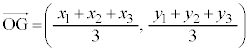
[証明] 2点A,Bの中点Mの位置ベクトルは、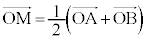
三角形ABCの重心Gは、線分CMを2:1に内分する点で、
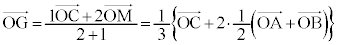
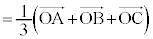
(証明終)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 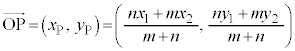 (図形と方程式で考えた内分点の座標と一致する。座標平面における内分・外分を参照)
(図形と方程式で考えた内分点の座標と一致する。座標平面における内分・外分を参照)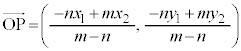 (図形と方程式で考えた外分の座標と一致する)
(図形と方程式で考えた外分の座標と一致する)