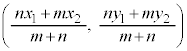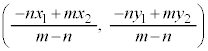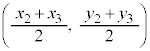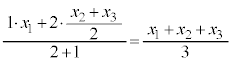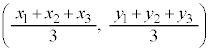座標平面における内分・外分 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
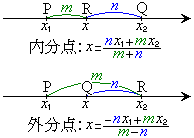1直線上に異なる3点P，Q，Rがあって、Rが線分PQ上にあって、PR：QR = m：n であるとき、Rは線分PQをm：nに内分すると言い、Rを内分点と言う。
また、Rが線分PQ上になく、PR：QR = m：nであるとき、Rは線分PQをm：nに外分すると言い、Rを外分点と言う。
数直線上に、2点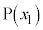
，
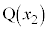があるとき、
線分PQをm：nに内分する点Rの座標は、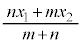
，
線分PQをm：nに外分する点Rの座標は、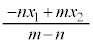
内分点では、内分比に出てくる数値の和が分母に来て、2点の座標の値にそれぞれの点から遠い方の比の数値をかけたものが分子に来る、という形をしています。
外分点は、外分比に出てくる数値の片方にマイナスをつけて、内分点と同様に考えればOK。
公式を証明しておきます。
線分PQをm：nに内分する点Rの座標をx，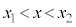
(
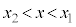の場合も同様です)だとして、
：
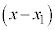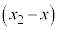= m：n より、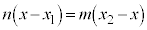
∴ 
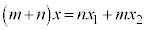
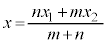
線分PQをm：nに外分する点Rの座標をx，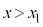
，
(
，
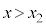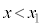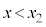の場合も同様です)だとして、
：
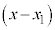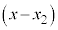= m：n より、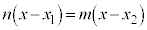
∴ 
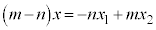
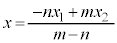
特に、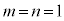
のとき、PQを1：1に内分する点(線分PQの中点)の座標は、
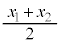となります。
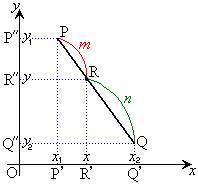座標平面上に2点P
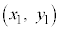，Q
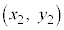があるとき、
線分PQをm：nに内分する点Rの座標は、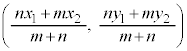
線分PQをm：nに外分する点Rの座標は、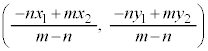
x座標だけ見れば、数直線上での内分点、外分点と同じです。y座標もxをyに変えたものになるだけです。
内分点R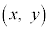
については、右図で、線分
をm：nに内分する点が
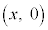，線分
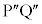をm：nに内分する点が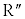
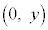と考えて、数直線上での内分点の公式を用いれば明らかでしょう。
外分点も同様です。
例．3点A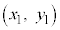
，B
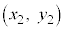，C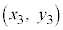
が与えられているとき、
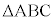の重心Gの座標を求めてみます(三角形の五心を参照)。
線分BCの中点Mの座標は、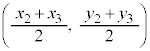
Gは線分AMを2：1に内分する点です。Gのx座標は、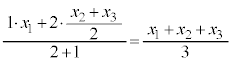
同様にGのy座標も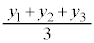
よって、重心Gの座標は、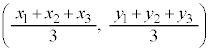
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。