�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�y�L���z�L���͂����܂łł��B
(3) ����π��̓_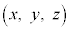 �̓_������������π�̕������́A�@���x�N�g����
�̓_������������π�̕������́A�@���x�N�g����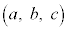 �Ƃ��āA
�Ƃ��āA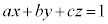
�_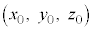 �ƕ���π�Ƃ̋���d�́A
�ƕ���π�Ƃ̋���d�́A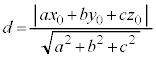
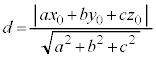
(1) ����π��̃x�N�g��
��������ƁA
�����ŁA
(�t�́A���܂̎��ό`���t�ɂ��ǂ邱�Ƃɂ��A�@���̂悤�ɏ�����̂ŁA�_P��3�_A�CB�CC���ʒu���镽��π��ɑ��݂��܂�)
(2) (1)�̇@�����A
����āA����π��̓_P�̈ʒu�x�N�g�����݂����������Ƃ��āA
�������܂��B
�����ŁA
�B�������ʂ�\���������ł��B
��
�D�������W��Ԃɂ����镽�ʂ̕������ł��B���ʂ̕�������x�Cy�Cz�̌W����x�����Ay�����Az�����Ƃ���x�N�g��
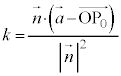
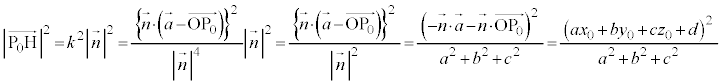 �@(�� �C)
�@(�� �C)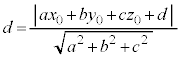
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��w�y�w�m ���������t���I
���n��w�l�b�g�m��w�y�w�m
(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B
���n��w�l�b�g�m��w�y�w�m
(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B