�����e�ʂ̌����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�d�וۑ����F�Ǘ������n�ɂ����ẮA�����̑O����d���̑��a�͈��ɂȂ�B
�Ód�e��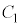 �C
�C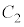 �C����C
�C����C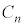 ���R���f���T�[������ڑ������Ƃ��������e��C�́A
���R���f���T�[������ڑ������Ƃ��������e��C�́A
�Ód�e��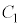 �C
�C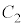 �C����C
�C����C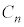 �̃R���f���T�[������ڑ������Ƃ��������e����C�Ƃ��āA
�̃R���f���T�[������ڑ������Ƃ��������e����C�Ƃ��āA
���w��������f���q�̔����Ɏ���܂ŁA�Ǘ������n�ɂ����ẮA�����̑O����d���̑��a�͈��ɂȂ邱�Ƃ������I�ɂ킩���Ă��܂��B���Ƃ����d�������݂��Ȃ������̈��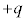 ���d����������Ƃ��ɂ́A
���d����������Ƃ��ɂ́A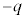 ���d�����ꏏ�ɐ�����̂ł��B
���d�����ꏏ�ɐ�����̂ł��B
���̎������d�וۑ����ƌ����܂��B
 �Ód�e��
�Ód�e��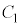 �C
�C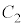 �C����C
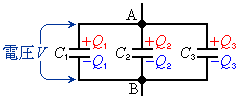
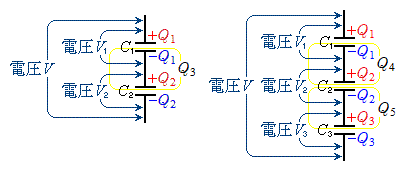
�C����C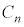 ���R���f���T�[��n�E�}�̂悤������ڑ�����ƁA�e�R���f���T�[��A�CB�Ԃ��d�ʍ���V�ŋ��ʂȂ̂ŁA�e�R���f���T�[�̒~�����d����
���R���f���T�[��n�E�}�̂悤������ڑ�����ƁA�e�R���f���T�[��A�CB�Ԃ��d�ʍ���V�ŋ��ʂȂ̂ŁA�e�R���f���T�[�̒~�����d����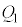 �C
�C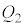 �C����C
�C����C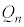 �Ƃ��āA
�Ƃ��āA
���A�S�R���f���T�[�̒~�����d���̑��a��Q�Ƃ��āA
n�̃R���f���T�[���Ód�e��C��1�̃R���f���T�[�ƌ���Ƃ��A
�Ƃ��āA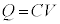 (�R���f���T�[���Q��)���������܂��B����C�������e���ƌ����܂��B
(�R���f���T�[���Q��)���������܂��B����C�������e���ƌ����܂��B
 �ŏ����d����~���Ă��Ȃ��Ód�e��
�ŏ����d����~���Ă��Ȃ��Ód�e��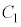 �C
�C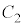 �C����C
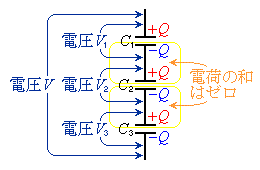
�C����C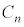 ���R���f���T�[��n�E�}�̂悤������ڑ�����ƁA�e�R���f���T�[�͋��ʂ��d��Q��~���܂��B�Ȃ��Ȃ�A�d�וۑ������A�אڂ���R���f���T�[�̊Ԃ��d�ׂ̘a�͂˂Ƀ[���ŁA����̃R���f���T�[�̋ɔ�
���R���f���T�[��n�E�}�̂悤������ڑ�����ƁA�e�R���f���T�[�͋��ʂ��d��Q��~���܂��B�Ȃ��Ȃ�A�d�וۑ������A�אڂ���R���f���T�[�̊Ԃ��d�ׂ̘a�͂˂Ƀ[���ŁA����̃R���f���T�[�̋ɔ�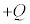 �������ƁA�t���̃R���f���T�[�̋ɔɂ�
�������ƁA�t���̃R���f���T�[�̋ɔɂ�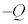 ���d��������邩��ł��B�e�R���f���T�[���d�ʍ���
���d��������邩��ł��B�e�R���f���T�[���d�ʍ���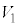 �C
�C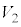 �C����C
�C����C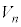 �Ƃ��āA
�Ƃ��āA
���A�S�R���f���T�[�̗��[���d�ʍ�(�e�d�ʍ��̑��a)��V�Ƃ��āA
n�̃R���f���T�[���Ód�e��C��1�̃R���f���T�[�ƌ���Ƃ��A
�Ƃ��āA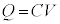 ���������܂��B����̏ꍇ�������e���́A����C�ɂȂ�܂��B
���������܂��B����̏ꍇ�������e���́A����C�ɂȂ�܂��B
�������A�R���f���T�[�̒���ڑ��̌������g����̂́A�R���f���T�[�Ԃ̕����̓d�ׂ��[���A�Ƃ����Ƃ������ł��B
 �X�C�b�`�̂Ȃ��ւ��Ȃǂɂ��A�R���f���T�[�Ԃɓd�ׂ��c���Ă���ꍇ������܂��B���̂Ƃ��́A�R���f���T�[��H�̌������Œ���E����f�ł��Ȃ��̂Œ��ӂ��K�v�ł��B
�X�C�b�`�̂Ȃ��ւ��Ȃǂɂ��A�R���f���T�[�Ԃɓd�ׂ��c���Ă���ꍇ������܂��B���̂Ƃ��́A�R���f���T�[��H�̌������Œ���E����f�ł��Ȃ��̂Œ��ӂ��K�v�ł��B
�Ⴆ�A�E�}�ŁA�Ód�e��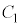 �C
�C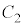 �̃R���f���T�[2�̏ꍇ�A
�̃R���f���T�[2�̏ꍇ�A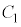 �C
�C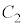 �̊Ԃ��d��
�̊Ԃ��d��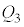 ���c���Ă����Ԃ�2�̃R���f���T�[�̗��[���d��V���������Ƃ��A
���c���Ă����Ԃ�2�̃R���f���T�[�̗��[���d��V���������Ƃ��A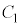 �̗����̋ɔ�
�̗����̋ɔ�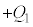 �C
�C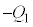 �C
�C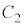 �̗����̋ɔ�
�̗����̋ɔ�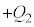 �C
�C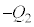 ���d���������āA
���d���������āA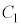 �̗��[���d����
�̗��[���d����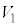 �C
�C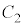 �̗��[���d����
�̗��[���d����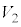 �ɂȂ����Ƃ��܂��B
�ɂȂ����Ƃ��܂��B
�@�{�A�~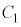 ���A
���A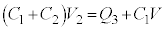 �@����B
�@����B
�� 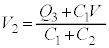
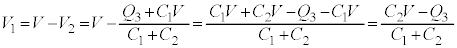 �@����C
�@����C �@�C�C�ɂ����āA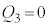 �̂Ƃ��Ɍ���A
�̂Ƃ��Ɍ���A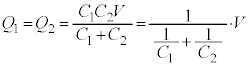 �ƂȂ��āA����̌������������܂��B�܂�A
�ƂȂ��āA����̌������������܂��B�܂�A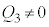 �ƂȂ�R���f���T�[�Ԃ��d�����c���Ă���ƁA����ڑ��Ɍ����Ă�����ɂȂ�܂���B
�ƂȂ�R���f���T�[�Ԃ��d�����c���Ă���ƁA����ڑ��Ɍ����Ă�����ɂȂ�܂���B
�����ŁA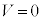 �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA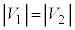 ��2�̃R���f���T�[���d���͓�����(����ڑ��̏�������)�̂ł����A�B�́A
��2�̃R���f���T�[���d���͓�����(����ڑ��̏�������)�̂ł����A�B�́A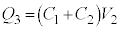 �ƂȂ�A
�ƂȂ�A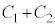 ��2�̃R���f���T�[�������e���Ƃ݂�ƁA����ڑ��Ɍ����Ă���2�̃R���f���T�[�����͕������A�Ƃ������Ƃ��N���肦�܂��B
��2�̃R���f���T�[�������e���Ƃ݂�ƁA����ڑ��Ɍ����Ă���2�̃R���f���T�[�����͕������A�Ƃ������Ƃ��N���肦�܂��B
�E�}�ŁA�Ód�e��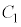 �C
�C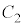 �C
�C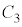 �̃R���f���T�[3�̏ꍇ�A
�̃R���f���T�[3�̏ꍇ�A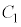 �C
�C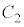 �̊Ԃ��d��
�̊Ԃ��d��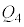 �C
�C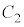 �C
�C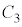 �̊Ԃ��d��
�̊Ԃ��d��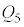 ���c���Ă����Ԃ�3�̃R���f���T�[�̗��[���d��V���������Ƃ��A
���c���Ă����Ԃ�3�̃R���f���T�[�̗��[���d��V���������Ƃ��A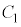 �̗����̋ɔ�
�̗����̋ɔ�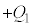 �C
�C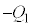 �C
�C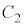 �̗����̋ɔ�
�̗����̋ɔ�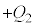 �C
�C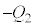 �C
�C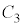 �̗����̋ɔ�
�̗����̋ɔ�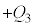 �C
�C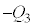 ���d���������āA
���d���������āA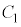 �̗��[���d����
�̗��[���d����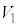 �C
�C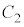 �̗��[���d����
�̗��[���d����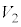 �C
�C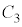 �̗��[���d����
�̗��[���d����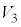 �ɂȂ�Ƃ���ƁA
�ɂȂ�Ƃ���ƁA
������(����E���q��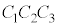 �Ŋ���)�A
�Ŋ���)�A
�D�C�E�C�F���A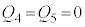 �̂Ƃ��Ɍ����āA
�̂Ƃ��Ɍ����āA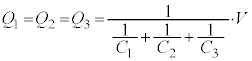 �ƂȂ��āA����̌������������܂��B�܂�A
�ƂȂ��āA����̌������������܂��B�܂�A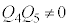 �ƂȂ�R���f���T�[�Ԃ��d�����c���Ă���ƁA����ڑ��Ɍ����Ă�����ɂȂ�܂���B�R���f���T�[�̐ڑ��́A��R�̐ڑ��ƈ���āA�������Ŕ��f���邱�Ƃ͂ł��Ȃ��Ɗo���Ă����Ă��������B
�ƂȂ�R���f���T�[�Ԃ��d�����c���Ă���ƁA����ڑ��Ɍ����Ă�����ɂȂ�܂���B�R���f���T�[�̐ڑ��́A��R�̐ڑ��ƈ���āA�������Ŕ��f���邱�Ƃ͂ł��Ȃ��Ɗo���Ă����Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 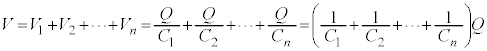
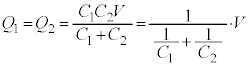 �ƂȂ��āA����̌������������܂��B�܂�A
�ƂȂ��āA����̌������������܂��B�܂�A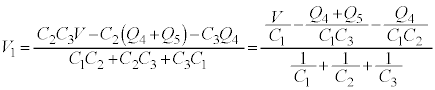 �@����D
�@����D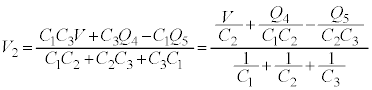 �@����E
�@����E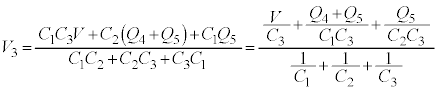 �@����F
�@����F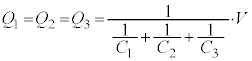 �ƂȂ��āA����̌������������܂��B�܂�A
�ƂȂ��āA����̌������������܂��B�܂�A