発散
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
ベクトル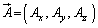
の各成分
，
，
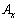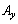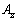がそれぞれx，y，zの関数になっているとき、
をベクトル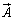
の発散(divergence)と言います。
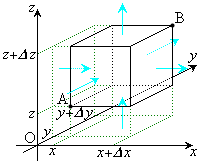右図のような直方体を考えます。直方体の各辺はx軸，y軸，z軸のどれかに平行で、x座標はxと
の間、y座標はyと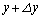
の間、z座標はzと
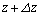の間にあります。
x方向について、xから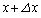
までの
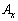の増分を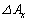
，y方向について、yから
までの
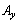の増分を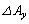
，z方向についてzから
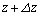までの
の増分を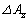
とすると、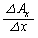
，
，
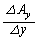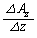は、ベクトル
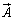の各成分のそれぞれの方向における平均変化率を表します。
ベクトル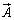
の流れのようなものを考えて、この流れがこの直方体を通過するとき、x方向の流れがy方向、z方向に回るものもあるし、y方向の流れがz方向、x方向に回るものもあるし、z方向の流れがx方向、y方向に回るものもあります。
ですが、点A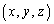
に隣接する3面から流入して、点B
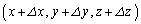に隣接する3面から流出する流れを考えると、ただ単にベクトルが流れていくだけであれば、3方向の平均変化率を加えたもの
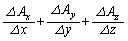は相殺されて0になるはずです。
ですが、この直方体の中で、ベクトルが湧き出したり、ベクトルが吸い込まれてしまう場合には0になりません。
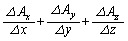は、この直方体の中で、ベクトルが湧き出したり吸い込まれてしまう分量を表しているのです。
ここで、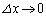
(y，zを固定)，
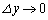(z，xを固定)，
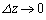(x，yを固定)としたものが、
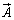の発散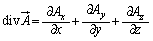
になります。
つまり、発散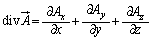
は、空間内のある点
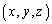において、微小な立方体を考えたときに、この直方体内で湧き出したり吸い込まれたりしたベクトル
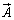の変化率を表しています。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 