�K�E�X�̖@���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�d�E�̑傫���ƁA�d�E�̌����ɐ����Ȗʂ��ʐ������������̂��d�C�͐��̑��{����\���B������K�E�X�̖@���ƌ����B
�^�ɂ����āA�d��q����L�т��d�C�͐��̑��{����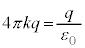 �{(�A���A
�{(�A���A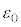 �͐^��̗U�d���A
�͐^��̗U�d���A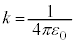 )�B
)�B
�_�d��q������r���ꂽ�_�ɂ����d�E�̋���E�́A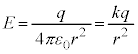
�K�E�X�̖@���ɂ��A�d�C�͐��̖��x���d�E�̋����ł��B
�^���_�d��q��1�u����Ă���Ƃ��āA�����_�d��������d�E���l���Ă݂܂��B
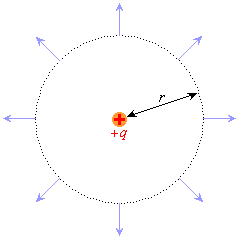 ��Ԃ̑Ώ̐�����A�_�d��q��������r�̂Ƃ���A���ar�̋��ʏ�̓_�ł́A�ǂ��ł������������d�E�ɂȂ�͂��ł��B�܂�A�d�C�͐��̖��x���������Ȃ�͂��ł��B
��Ԃ̑Ώ̐�����A�_�d��q��������r�̂Ƃ���A���ar�̋��ʏ�̓_�ł́A�ǂ��ł������������d�E�ɂȂ�͂��ł��B�܂�A�d�C�͐��̖��x���������Ȃ�͂��ł��B
�܂��A�d�C�͐������d������o�����d���ɏI�[����܂ő�����������������܂���B���ʏ���d�C�͐��̖��x���������Ȃ�̂ł���Ar��傫�����Ă����Ƃ��A���̋��ʂ��ʐ�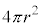 �ɔ���Ⴕ���d�C�͐��̖��x���������Ȃ�A�d�E�̋����͎�܂�ƍl����̂����R�ł��B����ɁA�d�C�͐��̖��x�A�����A�d�E�̋���E���_�d���̓d�C��q�ɔ�Ⴗ��ƍl����̂����R�ł��B�܂�A
�ɔ���Ⴕ���d�C�͐��̖��x���������Ȃ�A�d�E�̋����͎�܂�ƍl����̂����R�ł��B����ɁA�d�C�͐��̖��x�A�����A�d�E�̋���E���_�d���̓d�C��q�ɔ�Ⴗ��ƍl����̂����R�ł��B�܂�A
�^�ŁA���̔��萔��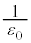 �Ƃ���ƁA
�Ƃ���ƁA
���ꂪ�^�Ō��_O�ɒu���ꂽ�_�d��q������r���ꂽ�_P�ɍ���d�E�̋�����^���܂��B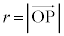 �ł��B
�ł��B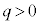 �ł���A������̐����_�d������Ԓ��̂ǂ��ɒu���Ă��˗��������̂ŁA�d�E�̌����́A
�ł���A������̐����_�d������Ԓ��̂ǂ��ɒu���Ă��˗��������̂ŁA�d�E�̌����́A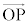 �̌����ł��B�_�d��q����͕��ˏ���d�E�x�N�g�������Ԃ��ƂɂȂ�܂��B
�̌����ł��B�_�d��q����͕��ˏ���d�E�x�N�g�������Ԃ��ƂɂȂ�܂��B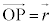 �Ƃ��āA�d�E�̌������܂߂ăx�N�g���ŕ\���ƁA�d�E�x�N�g��
�Ƃ��āA�d�E�̌������܂߂ăx�N�g���ŕ\���ƁA�d�E�x�N�g��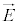 �́A
�́A
�ƕ\�����Ƃ��ł��܂��B
���萔�̒��ɏo�Ă���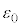 ���^��̗U�d���ƌ����܂��B
���^��̗U�d���ƌ����܂��B
�Ə�����̂ŁA�^��̗U�d���̒P�ʂ́A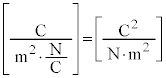 (
(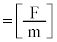 �C
�C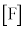 �́A�R���f���T�[�̌����F
�́A�R���f���T�[�̌����F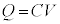 �ɏo�Ă���Ód�e��C�̒P�ʁF�t�@���b�h�ł��B
�ɏo�Ă���Ód�e��C�̒P�ʁF�t�@���b�h�ł��B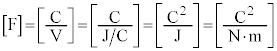 �ł�)�ƂȂ�܂��B
�ł�)�ƂȂ�܂��B
�A�́A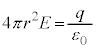 �ƌ��邱�Ƃ��ł��܂��B
�ƌ��邱�Ƃ��ł��܂��B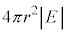 �͋��ʂ��ʐ����d�C�͐��̖��x�����������̂ŁA���ʂ�ʉ߂����d�C�͐��̖{����\���܂��B(2)�ɏ������悤�ɁA�d�C�͐������d������o�����đ���������������������d���Ɍ������̂ŁA
�͋��ʂ��ʐ����d�C�͐��̖��x�����������̂ŁA���ʂ�ʉ߂����d�C�͐��̖{����\���܂��B(2)�ɏ������悤�ɁA�d�C�͐������d������o�����đ���������������������d���Ɍ������̂ŁA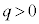 �̏ꍇ�A�_�d��q�����
�̏ꍇ�A�_�d��q�����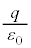 (
(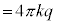 )�{���d�C�͐����o�čs���A
)�{���d�C�͐����o�čs���A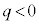 �̏ꍇ�ɁA�_�d��q��
�̏ꍇ�ɁA�_�d��q��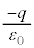 (
(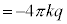 )�{���d�C�͐����I�[���܂��B���Z�̋��ȏ��ł́A���̎������K�E�X�̖@���ƌĂт܂��B
)�{���d�C�͐����I�[���܂��B���Z�̋��ȏ��ł́A���̎������K�E�X�̖@���ƌĂт܂��B
��1�@�^�ɂ����āA�ʐ�S�̕��ʏ���d��Q�����z���Ă���ꍇ�A���̕��ʂ��҂����蕢���Ȗʂ��l����ƁA�����ʐ���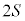 (��ʁA���ʂ̗��ʂ�����)�C
(��ʁA���ʂ̗��ʂ�����)�C
�K�E�X�̖@�����A���̕��ʂ̏㑤�A�������d�E�̋���(�[�̌��ʂ�����)�A�܂��d�C�͐��̖��x�́A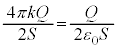
�U�d��ε�̕������ł́A�d�E�̋�����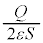 �ƂȂ�܂��B
�ƂȂ�܂��B
��2�@�^�ŁA�ʐ�S�̋ɔ��Ԋud���ւ��Ă�2�����s�Ɍ������킹��B�Е��̋ɔ�A���d��Q�C��������̋ɔ�B���d��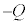 ��u���B
��u���B
���ɔ̊Ԃ��d�E�́A�e�ɔ�����d�E�̘a�ƂȂ�AA���d����B���d�����AA��B�̕������d�E����邩��A��1���A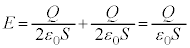
����AAB�Ԃ��d����V�Ƃ���ƁA�ɔԂ��d�E�͈�l������A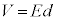
�� 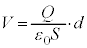 ��
�� 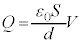
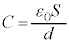 (���s�R���f���T�[���Ód�e��)�Ƃ����ƁA�R���f���T�[�̌����F
(���s�R���f���T�[���Ód�e��)�Ƃ����ƁA�R���f���T�[�̌����F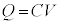 ��������܂��B
��������܂��B
�ɔԂɗU�d��ε�̕��������݂���ꍇ�ɂ́A�Ód�e���F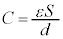 �Ƃ��āA
�Ƃ��āA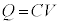 �ƂȂ�܂��B��U�d��
�ƂȂ�܂��B��U�d��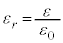 ��p���āA�Ód�e����
��p���āA�Ód�e����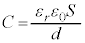 �Ə������Ƃ��ł��܂��B
�Ə������Ƃ��ł��܂��B
�^�ł͂Ȃ��A�U�d��ε�̕������ŁA���_O�ɒu���ꂽ�_�d��q���A����r���ꂽ�_�ɍ���d�E�̋����́A
�ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 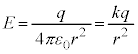
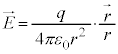 �@(
�@(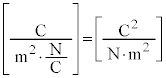 (
(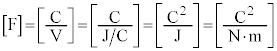 �ł�)�ƂȂ�܂��B
�ł�)�ƂȂ�܂��B