���Ȃ��@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�s�A�m��M�^�[�̂悤�Ȍ��y��̃`���[�j���O(���������킹����)���s���Ƃ��A2�̌��œ��������̉���炵�āA������A������A������A������ƕ������Ă�����A2�̌��ʼn����������Ă��Ȃ��A�����Ō��̒����������ƁA����A���̂����ԉ��т��Ă��āA���킠�`��A���킠�`��A���킠�`��A�ƂȂ�A�����������Ă���ɏ]���A���킠�`�`�`��A���킠�`�`�`��A�ƂȂ�A���ɁA���̂����Ȃ��Ȃ��Đ������������Ă���ƁA�`���[�j���O�����ł��B���̂��������Ȃ��ł��B���́A�@�B���g���ă`���[�j���O���邩���m��܂��A���Ȃ���Ȃ��炤�Ȃ肪�Ȃ��Ȃ�悤�ɒ�������A�Ƃ����̂��{���̃`���[�j���O�ł��B
���Ȃ�́A�����ɈقȂ�2���U�����̉����ɖ炷�Ɗϑ�����܂��B
����t �C�ʒu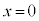 �ɂ�����A2���U����
�ɂ�����A2���U����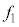 �C
�C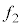 �̉��g���ψ�
�̉��g���ψ�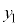 �C
�C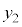 ��\�������g�̎��́A�U����A�C������v�Ƃ��A�����ʑ����l���Ȃ����Ƃɂ���ƁA
��\�������g�̎��́A�U����A�C������v�Ƃ��A�����ʑ����l���Ȃ����Ƃɂ���ƁA
����2�g���d�ˍ��킳���ƁA
���̒��ŁA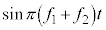 �́A
�́A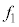 ��
��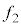 ���߂��l�̎��ɂ́A�قڌ��̉��g
���߂��l�̎��ɂ́A�قڌ��̉��g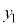 �C
�C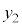 �̐U����\���܂��B
�̐U����\���܂��B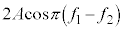 �����̉��g���U���̂悤�ȓ��������܂��B
�����̉��g���U���̂悤�ȓ��������܂��B
 �Ⴆ�A
�Ⴆ�A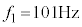 �C
�C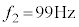 �Ƃ���ƁA
�Ƃ���ƁA
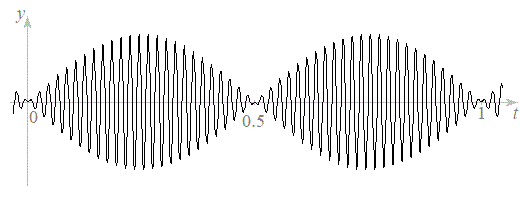
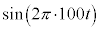 �́A���̉��g���U�����ɋ߂�100Hz�̐U����\���Ă��܂��B�}������ƁA�E�}�̂悤�ɂȂ�܂��B
�́A���̉��g���U�����ɋ߂�100Hz�̐U����\���Ă��܂��B�}������ƁA�E�}�̂悤�ɂȂ�܂��B
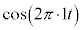 �́A1Hz�̐U����\���܂����A�l�Ԃ̎��ɕ�������100Hz�̉��͋���ƂȂ��ĕ������A�l�Ԃ̎��͂��Ȃ���A�U����2��ɔ�Ⴗ���g�̃G�l���M�[�̌`�A
�́A1Hz�̐U����\���܂����A�l�Ԃ̎��ɕ�������100Hz�̉��͋���ƂȂ��ĕ������A�l�Ԃ̎��͂��Ȃ���A�U����2��ɔ�Ⴗ���g�̃G�l���M�[�̌`�A
�Ŋ��m����̂ŁA���Ȃ���U���́A2Hz�̐U���̂悤�ɕ������܂��B�����ŁA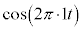 �́A1Hz�̐U���ł����A�u���Ȃ���U�����v�ƌ����Ƃ��́A2Hz (
�́A1Hz�̐U���ł����A�u���Ȃ���U�����v�ƌ����Ƃ��́A2Hz (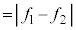 )�ƍl���܂��B
)�ƍl���܂��B
�܂�A2�̋߂��U����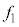 �C
�C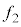 �̉��g���d�ˍ��킹���Ƃ��̂��Ȃ���U�����́A
�̉��g���d�ˍ��킹���Ƃ��̂��Ȃ���U�����́A
�܂��A���Ȃ�������́A
�ł�(��Βl������̂�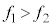 ��
��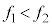 �͂�����̏ꍇ�ł������̒l�ɂ��邽�߂ł�)�B
�͂�����̏ꍇ�ł������̒l�ɂ��邽�߂ł�)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B