�f���q(����3)����̂Â��ł��B
1967�N�A���C���o�[�O�ƃT�������Ɨ��ɓd���C�͂Ǝア�͂�I�Ɉ������_(�d�㓝�ꗝ�_�ƌĂ�܂�)���o���܂����BSU(2)�~U(1)�Ƃ����Q�[�W�Q�ɏ]���Q�[�W���_�ł��B�O�q�̂悤�ɓd����̑��ݍ�p��}��闱�q�͎���0�̌��q�ł��B �̃N���C���E�S���h���̕��������d���g�̔g���������ɂȂ��Ă��܂�(�Q�[�W�ϊ����g���������ɂȂ��Ă���)�̂ŁA�Q�[�W�s�ϐ��̗v���ɂ����q�͎��ʂ����Ă܂���B�d���g�͉��g��2�̎��R�x�������Ă��āA
�̃N���C���E�S���h���̕��������d���g�̔g���������ɂȂ��Ă��܂�(�Q�[�W�ϊ����g���������ɂȂ��Ă���)�̂ŁA�Q�[�W�s�ϐ��̗v���ɂ����q�͎��ʂ����Ă܂���B�d���g�͉��g��2�̎��R�x�������Ă��āA �̉�]�Ώ̐�
�̉�]�Ώ̐� �������܂��B�d�㗝�_�ł͓d��Q�ł͂Ȃ��A��A�C�\�X�s���̑�3������
�������܂��B�d�㗝�_�ł͓d��Q�ł͂Ȃ��A��A�C�\�X�s���̑�3������ �Ƃ��āA�㒴�d��
�Ƃ��āA�㒴�d�� �̑Ώ̐�
�̑Ώ̐� ���l���܂��B�܂��A��A�C�\�X�s����Ԃ̕ϊ���
���l���܂��B�܂��A��A�C�\�X�s����Ԃ̕ϊ��� �Ώ̐��������A�Q�[�W��
�Ώ̐��������A�Q�[�W�� �̓p�E���s���p����
�̓p�E���s���p���� �̂悤�ɕ\����܂��B�N�H�[�N�ƃ��v�g���̂����A�������̂��̂�
�̂悤�ɕ\����܂��B�N�H�[�N�ƃ��v�g���̂����A�������̂��̂� �̃Q�[�W�ϊ�����̂ŁA�����͋��ϔ���
�̃Q�[�W�ϊ�����̂ŁA�����͋��ϔ��� (
( �͌����萔)�ƂȂ�A�Q�[�W��
�͌����萔)�ƂȂ�A�Q�[�W�� �Ƒ��ݍ�p���܂�(�E�����̂��̂́A�Q�[�W�s�ςő��ݍ�p���Ȃ�)�B������down�N�H�[�N�ɑ��鑊�ݍ�p��������ŁA�������ƉE�����ƂňقȂ�̂ŁA�ア���ݍ�p�ł̓p���e�B�[�ۑ����j��܂��B
�Ƒ��ݍ�p���܂�(�E�����̂��̂́A�Q�[�W�s�ςő��ݍ�p���Ȃ�)�B������down�N�H�[�N�ɑ��鑊�ݍ�p��������ŁA�������ƉE�����ƂňقȂ�̂ŁA�ア���ݍ�p�ł̓p���e�B�[�ۑ����j��܂��B ��
�� �̎��R�x�ɂ��3��̃Q�[�W���q
�̎��R�x�ɂ��3��̃Q�[�W���q �C
�C �C
�C ���o�Ă��܂����A�Q�[�W���q�ł���Ύ���0�̂͂��Ȃ̂ɁA����3��̗��q�͑傫�Ȏ��ʂ������A���̂��߂Ɏア���ݍ�p�̓��B�����͔��ɒZ���Ȃ�܂��B1964�N�ɁA�C�M���X�̃q�b�O�X���Q�[�W�Ώ̐��̔j��ɂ���āA�Q�[�W���q�����ʂ��l������A�Ƃ����q�b�O�X�@�\�̗��_����܂����B���C���o�[�O�ƃT�����͂��̍l�������̂����āA
���o�Ă��܂����A�Q�[�W���q�ł���Ύ���0�̂͂��Ȃ̂ɁA����3��̗��q�͑傫�Ȏ��ʂ������A���̂��߂Ɏア���ݍ�p�̓��B�����͔��ɒZ���Ȃ�܂��B1964�N�ɁA�C�M���X�̃q�b�O�X���Q�[�W�Ώ̐��̔j��ɂ���āA�Q�[�W���q�����ʂ��l������A�Ƃ����q�b�O�X�@�\�̗��_����܂����B���C���o�[�O�ƃT�����͂��̍l�������̂����āA �C
�C �����ʂ������Ƃ�������܂����B
�����ʂ������Ƃ�������܂����B
���C���o�[�O�E�T�������_�ł́A�Q�[�W���q�̏�ϕ�� �Ƃ��āA�Î~�G�l���M�[���������q�b�O�X�E�|�e���V�����G�l���M�[(�O���t�ɕ`�����`�烁�L�V�J���E�n�b�g�E�|�e���V�����ƌĂ�܂�)�A
�Ƃ��āA�Î~�G�l���M�[���������q�b�O�X�E�|�e���V�����G�l���M�[(�O���t�ɕ`�����`�烁�L�V�J���E�n�b�g�E�|�e���V�����ƌĂ�܂�)�A
�ƁA���v�g���A�N�H�[�N�Ƃ̑��ݍ�p�ׂ܂��B�@�́A �̂Ƃ���
�̂Ƃ��� (
( �ŁA�Ώ̐������݂�����)������Ȃ荇���̈ʒu�ɂȂ�܂��B�ł����A
�ŁA�Ώ̐������݂�����)������Ȃ荇���̈ʒu�ɂȂ�܂��B�ł����A (μ�F������)�ɂȂ��Ă��܂��ƁC
(μ�F������)�ɂȂ��Ă��܂��ƁC �ɂ�����V���ɏ��l�����A����Ȃ荇���̈ʒu���ω����܂��B
�ɂ�����V���ɏ��l�����A����Ȃ荇���̈ʒu���ω����܂��B �Ƃ����āA������^����Ғl�ƌ����܂��B�܂�A�^��́A�G�l���M�[���[���̏�Ԃɂ���̂ł͂Ȃ��A�L���̊��Ғl������ϕ����Ԃɖ����Ă���Ƃ����̂ł��B
�Ƃ����āA������^����Ғl�ƌ����܂��B�܂�A�^��́A�G�l���M�[���[���̏�Ԃɂ���̂ł͂Ȃ��A�L���̊��Ғl������ϕ����Ԃɖ����Ă���Ƃ����̂ł��B �̂Ƃ��́A�Ώ̐��̂���
�̂Ƃ��́A�Ώ̐��̂��� �̏�Ԃ��s����ŁA
�̏�Ԃ��s����ŁA (�ꂪ�A��������
(�ꂪ�A�������� �C
�C �ƂȂ�A��]�Ώ̐��̎���ꂽ���)�Ɉڍs���A��ԑS�̂ɂ킽���āA�^�Ώ̐��̂����Ԃ���Ώ̐��̕��ꂽ��ԂɈڍs���Ă��܂��܂��B����������I�Ώ̐��̔j���ƌ����܂��B���̂Ƃ��̇@��
�ƂȂ�A��]�Ώ̐��̎���ꂽ���)�Ɉڍs���A��ԑS�̂ɂ킽���āA�^�Ώ̐��̂����Ԃ���Ώ̐��̕��ꂽ��ԂɈڍs���Ă��܂��܂��B����������I�Ώ̐��̔j���ƌ����܂��B���̂Ƃ��̇@�� �Ƃ��������A
�Ƃ��������A �ƌ���ƁA
�ƌ���ƁA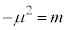 �����ʂ�^���A�Q�[�W���q�ƃ��v�g���A�N�H�[�N�Ƃ̑��ݍ�p�̑傫������A�E�B�[�N�{�\���A���v�g���A�N�H�[�N�̎��ʂ����܂�܂��B���̂��炭����q�b�O�X�@�\�ƌ����܂��B�q�b�O�X�@�\�ɂ���āA�E�B�[�N�E�{�\���͎��ʂ��l�����܂��B
�����ʂ�^���A�Q�[�W���q�ƃ��v�g���A�N�H�[�N�Ƃ̑��ݍ�p�̑傫������A�E�B�[�N�{�\���A���v�g���A�N�H�[�N�̎��ʂ����܂�܂��B���̂��炭����q�b�O�X�@�\�ƌ����܂��B�q�b�O�X�@�\�ɂ���āA�E�B�[�N�E�{�\���͎��ʂ��l�����܂��B
�C���t���[�V�����F���_�ł́A�r�b�O�E�o������̉F�������܂����G�l���M�[�̍�����Ԃ������̂��A�F�����₦�đs��ȑ��]�ڂ��N�����A ��
�� �ň��肾�����^�A
�ň��肾�����^�A ��
�� �ň���ƂȂ�悤�ɑ��]�ڂ��A�f���q�����ʂ��l�������A�ƍl�����Ă��܂��B���C���o�[�O�E�T�����̗��_�́A1970�N��ɓ���A�I�����_�̃g�z�[�t�g�ɂ���Ă��荞�݉\�Ȃ��Ƃ�������A1983�N�A�z�q�E���z�q�Փˎ����̒���W�{�\���AZ�{�\���̔����A
�ň���ƂȂ�悤�ɑ��]�ڂ��A�f���q�����ʂ��l�������A�ƍl�����Ă��܂��B���C���o�[�O�E�T�����̗��_�́A1970�N��ɓ���A�I�����_�̃g�z�[�t�g�ɂ���Ă��荞�݉\�Ȃ��Ƃ�������A1983�N�A�z�q�E���z�q�Փˎ����̒���W�{�\���AZ�{�\���̔����A
����������Ď�����܂����B
�A���A���`���̂ɂ͓d���g(���͐�)���N���ł����A���`���̂����S�������������Ƃ����}�C�X�i�[���ʂ��m���Ă��āA���q�������I�Ȏ��ʂ����ꍇ������܂��B���������u�����I�Ώ̐��̔j��v�Ƃ����A�C�f�A�́A�암�z��Y���}�C�X�i�[���ʂ��璅�z�������̂ƌ����Ă��܂��B
�ꎞ�́A�N�H�[�N�͕X�I�ɉ��z���ꂽ���w�I���f���ɉ߂��Ȃ��A�Ƃ����ӌ�������܂����B�����ŁA�K�C�K�[�ƃ}�[�X�f���������q�Ƀ����ĂČ��q�j�̓����\������͂����悤�ɁA1968�N�A�j�q�ɍ��G�l���M�[�̓d�q�ĂĊj�q�̓����\���ׂ����(�[����e���U���ƌ����Ă��܂�)���s���܂���(���̎����́A�O�q�̃X�^���t�H�[�h��̐��`������ŁA�𑜓x���グ�Ĕ��\���ׂ邽�߂ɃG�l���M�[��傫�����ēd�q�g�̔g���F ������ɒZ��������ǂ��s�������u�ōs���܂���)�B�����A�N�H�[�N���������q��̂��̂Ȃ�d�q���e���U�������Ɨ\�z����܂����A�U���͔�e���U���ŁA�������j�q�̓����ɂ́A�N�H�[�N�̉e���ƍl������3�̌����Ό��_��������̂́A�^���ʂ�3�̃N�H�[�N��
������ɒZ��������ǂ��s�������u�ōs���܂���)�B�����A�N�H�[�N���������q��̂��̂Ȃ�d�q���e���U�������Ɨ\�z����܂����A�U���͔�e���U���ŁA�������j�q�̓����ɂ́A�N�H�[�N�̉e���ƍl������3�̌����Ό��_��������̂́A�^���ʂ�3�̃N�H�[�N�� ���̉^���ʂ����̂ł͂Ȃ��A�L�������^���ʕ��z�������Ă���A�ʂ̗��q�̑��݂��������錋�ʂƂȂ�܂����B���̕ʂ̗��q�͓d�q�Ƒ��ݍ�p�����A�O���[�I��(�N�H�[�N���m���܂Ƃ߂Ă���d�׃[���̗��q)�ƍl�����A�j�q��(�]���Č��q�j��)�ŃN�H�[�N���O���[�I�����z�����Ȃ��痬���I�ɓ����Ă���悤�ȃC���[�W�ł��B��������������1969�N�Ƀt�@�C���}���ɂ���čl����ꂽ���̂��p�[�g���͌^�ƌĂ�Ă��܂��B�p�[�g���͌^�ɂ��U���f�ʐς𐳊m�Ɍv�Z���邱�Ƃ��ł��܂��B�������Ȃ���A���݂Ɏ���܂ŃN�H�[�N�̓����\���܂ł͌����Ă��܂���B
���̉^���ʂ����̂ł͂Ȃ��A�L�������^���ʕ��z�������Ă���A�ʂ̗��q�̑��݂��������錋�ʂƂȂ�܂����B���̕ʂ̗��q�͓d�q�Ƒ��ݍ�p�����A�O���[�I��(�N�H�[�N���m���܂Ƃ߂Ă���d�׃[���̗��q)�ƍl�����A�j�q��(�]���Č��q�j��)�ŃN�H�[�N���O���[�I�����z�����Ȃ��痬���I�ɓ����Ă���悤�ȃC���[�W�ł��B��������������1969�N�Ƀt�@�C���}���ɂ���čl����ꂽ���̂��p�[�g���͌^�ƌĂ�Ă��܂��B�p�[�g���͌^�ɂ��U���f�ʐς𐳊m�Ɍv�Z���邱�Ƃ��ł��܂��B�������Ȃ���A���݂Ɏ���܂ŃN�H�[�N�̓����\���܂ł͌����Ă��܂���B
�דd���q�̎U���f�ʐς̌v�Z���s���ƁA�U���f�ʐς͊�{���q�̓d�ׂ�2��ɔ�Ⴕ�܂��B�d�q�E�j�q�Փˎ����̌��ʂł́A�z�q�A�����q�̓d�ׂ�2��́A�e�X �C
�C �ɂȂ�܂��B�N�H�[�N�͌^�ł́A�z�q��up�N�H�[�N(�d��
�ɂȂ�܂��B�N�H�[�N�͌^�ł́A�z�q��up�N�H�[�N(�d�� )2��down�N�H�[�N(�d��
)2��down�N�H�[�N(�d�� )1����ł��Ă��āA�d�ׂ�2��̘a���v�Z����ƁA
)1����ł��Ă��āA�d�ׂ�2��̘a���v�Z����ƁA
�����q��up�N�H�[�N1�Adown�N�H�[�N2����ł��Ă���̂ŁA�d�ׂ�2��̘a���v�Z����ƁA
�ƂȂ�A�������ʂƈ�v���A����������N�H�[�N�E���f���̗L�������m�F�ł��܂����B
�d�q�Ɨz�d�q���Փ˂�����Ƃ��A�d�q�̎��ʂ� �Ƃ��āA���҂͐Î~�G�l���M�[
�Ƃ��āA���҂͐Î~�G�l���M�[ �������Ă���A�Փ˂ɂ���Ĕ���������q�̃G�l���M�[�͗��҂̉^���G�l���M�[�̘a��K�Ƃ��āA
�������Ă���A�Փ˂ɂ���Ĕ���������q�̃G�l���M�[�͗��҂̉^���G�l���M�[�̘a��K�Ƃ��āA �ƂȂ�܂��B���̒l�����܂�傫���Ȃ���A�����������q�͍Ăѓd�q�E�z�d�q�ɖ߂�܂��B�ł����Aup�N�H�[�Nu�Adown�N�H�[�Nd�̎��ʂ��e�X
�ƂȂ�܂��B���̒l�����܂�傫���Ȃ���A�����������q�͍Ăѓd�q�E�z�d�q�ɖ߂�܂��B�ł����Aup�N�H�[�Nu�Adown�N�H�[�Nd�̎��ʂ��e�X �C
�C (
( )�Ƃ��āA
)�Ƃ��āA �ɂȂ�ƁA
�ɂȂ�ƁA
�Ƃ����������N���܂��B �ɂȂ�ƁA
�ɂȂ�ƁA
�ʗ��q�̎��ʂ� �Ƃ��āA
�Ƃ��āA �ɂȂ�ƁA
�ɂȂ�ƁA
�Ƃ��������������܂��B���̂Ƃ��A�~���[���q�����̔����f�ʐς� �Ƃ���ƁA
�Ƃ���ƁA
�ł��Bstrange�N�H�[�Ns�̔���
���܂߂āAu�Cd�Cs�̓d�ׂ� �C
�C �C
�C �Ȃ̂ŁA�n�h�������������锽���̒f�ʐ�
�Ȃ̂ŁA�n�h�������������锽���̒f�ʐ� �́A
�́A
�ƂȂ�A ��
�� �̔�R�́A
�̔�R�́A
�ƂȂ�̂ł����A��q����charm�N�H�[�N�̎��ʂ� �Ƃ��āA
�Ƃ��āA ���������ȃG�l���M�[�Ŏ������s���Ă��������ɂ́A�������ʂ�
���������ȃG�l���M�[�Ŏ������s���Ă��������ɂ́A�������ʂ� �ł����B�����ŁA�N�H�[�N�̐F�ɂ��Ⴂ�ɂ��A
�ł����B�����ŁA�N�H�[�N�̐F�ɂ��Ⴂ�ɂ��A �C
�C �C
�C �C
�C �C
�C �C
�C �C
�C �C
�C �C
�C ���قȂ闱�q�ƍl���邱�Ƃɂ���ƁA
���قȂ闱�q�ƍl���邱�Ƃɂ���ƁA
 �C
�C
�܂��A�z�q�E���z�q�Փˎ����ł́A�N�H�[�N�E���N�H�[�N�̃y�A�A���Ԏq�A�n�h�����A���v�g�����V�����[�̂悤�ɐ��������̂ł����A�z�q�E���z�q�Փˎ����̉�͂���A�N�H�[�N���m�̊Ԃɓ��������͂́A�N�H�[�N�Ԃ̋������������Ȃ�Ə������Ȃ�A�������傫���Ȃ�Ƒ傫���Ȃ邱�Ƃ��킩���Ă��܂��B������Q�ߓI���R���ƌ����܂��B�Փ˂ɂ�萶�����N�H�[�N�Ɣ��N�H�[�N�̃y�A�́A�S���R�̂悤�Ȃ��̂Ō���Ă��ăN�H�[�N������Ă����ƈ��������͂��傫���Ȃ�A����ɗ���悤�Ƃ���ƁA�d�C�͂ł͓d�C�͐��͖����ɒ����L�т܂����A�����͂̏ꍇ�͐^��ɋ����̗͂͐����i��悤�Ȍ��ʂ������āA�S���R���L�т�ƃS���R����A�ꂽ�Ƃ���ɃN�H�[�N�Ɣ��N�H�[�N���������A�S���R�̗��[�ɕK���N�H�[�N�����ꗼ�҂̐F�ׂ̏d�ˍ��킹�����ɂȂ�悤�ɒ��Ԏq���ł��܂��B���ꂪ���X�ɋN����̂ŁA���Ԏq���V�����[�̂悤�ɕ��o����܂��B����ŁA�N�H�[�N���m���߂Â��ƁA�N�H�[�N���O���[�I������o���ĐF���ς�����(�Ⴆ�A�ԃN�H�[�N���ԁ{���̃O���[�I������o���ĐN�H�[�N�ɕς��A�N�H�[�N���ԁ{���̃O���[�I�����z�����ĐԃN�H�[�N�ɕς��)�ɂ���āA�^��ɂɂ��N�H�[�N�̎��͂ɂł��������̃N�H�[�N�̐F�ׂ̏d�ˍ��킹�����ɂȂ�A�����͂���܂��Ă��܂��A�Ƃ����悤�ɐ�������Ă��܂��B�O�q�̃p�[�g���͌^�́A�Q�ߓI���R���ɂ��N�H�[�N�Ԃ̗͂���܂邱�Ƃ�O��Ƃ����l�����ł��B
�d�q�A�d�q�j���[�g���m�����v�g��(�y���q)�̑g���1����A�ʗ��q�A�ʃj���[�g���m�̑g�����v�g���̑�2����ƌ����܂��B1970�N���܂łɁA�N�H�[�N�́Aup�N�H�[�Nu��down�N�H�[�Nd(u��d�ő�1����ƌ����܂�)�̑g�ƁAstrange�N�H�[�Ns����������Ă���A�o���I����3��ނ̃N�H�[�N�ō\������Ă���A�Ƃ���Ă��܂����B�܂��A���v�g����N�H�[�N�̎ア���ݍ�p�ɂ�����́A������݂̂ŋN����ƍl�����Ă��܂����B�Ƃ��낪�A������ (�E�B�[�N�E�{�\��
(�E�B�[�N�E�{�\�� ��
�� �ƕ��܂�)�����łȂ��A
�ƕ��܂�)�����łȂ��A �C
�C �̂悤�Ȕ������ϑ�����A����Ԃō����荇���Ĕ������N���邱�Ƃ��킩���Ă��܂����B1963�N�C�^���A�̃J�r�{�́Aup�N�H�[�N�ƑɂȂ�̂́Adown�N�H�[�N
�̂悤�Ȕ������ϑ�����A����Ԃō����荇���Ĕ������N���邱�Ƃ��킩���Ă��܂����B1963�N�C�^���A�̃J�r�{�́Aup�N�H�[�N�ƑɂȂ�̂́Adown�N�H�[�N ��strange�N�H�[�N
��strange�N�H�[�N ���d�Ȃ荇�����A
���d�Ȃ荇�����A (
( �C�J�r�{�p�ƌ����܂�)���Ǝ咣���܂����B1964�N�AK���Ԏq�̕����CP�Ώ̐�(���q�Ɣ����q�]������דd����ϊ�C�ƃp���e�B�ϊ�P�̐ςɊւ���Ώ̐�)���j��Ă��邱�Ƃ����������ƁA1973�N�A���ѐ��Ɖv��q�p�́ACP�Ώ̐��̔j���������邽�߂ɁA���݂��\������Ă������̂̓����������Ă��Ȃ���2�����strange�N�H�[�N�̑���A�܂��A��3����̃N�H�[�N��z�肵�āA�J�r�{�̍l�������g�����A3�s3���CKM�s��(�J�r�{�E���сE�v��s��)�����āA���n��(d�Cs�Cb)�̃N�H�[�N�̍�������n��̃N�H�[�N(u�Cc�Ct)�ɕ���A�Ƃ������_�\���܂����B
�C�J�r�{�p�ƌ����܂�)���Ǝ咣���܂����B1964�N�AK���Ԏq�̕����CP�Ώ̐�(���q�Ɣ����q�]������דd����ϊ�C�ƃp���e�B�ϊ�P�̐ςɊւ���Ώ̐�)���j��Ă��邱�Ƃ����������ƁA1973�N�A���ѐ��Ɖv��q�p�́ACP�Ώ̐��̔j���������邽�߂ɁA���݂��\������Ă������̂̓����������Ă��Ȃ���2�����strange�N�H�[�N�̑���A�܂��A��3����̃N�H�[�N��z�肵�āA�J�r�{�̍l�������g�����A3�s3���CKM�s��(�J�r�{�E���сE�v��s��)�����āA���n��(d�Cs�Cb)�̃N�H�[�N�̍�������n��̃N�H�[�N(u�Cc�Ct)�ɕ���A�Ƃ������_�\���܂����B
1974�N�A ������ō����ɉ������ꂽ�d�q�E�z�d�q�̏Փˎ����ŁAstrange�N�H�[�N�̑���ƂȂ�N�H�[�N���\�����q�Ƃ���A�`���[�����q�ƌĂ���A�̃n�h��������������A���̃N�H�[�N��charm�N�H�[�N�Ɩ�������܂����B���̂Ƃ��Acharm�N�H�[�N�̎��ʂ�
������ō����ɉ������ꂽ�d�q�E�z�d�q�̏Փˎ����ŁAstrange�N�H�[�N�̑���ƂȂ�N�H�[�N���\�����q�Ƃ���A�`���[�����q�ƌĂ���A�̃n�h��������������A���̃N�H�[�N��charm�N�H�[�N�Ɩ�������܂����B���̂Ƃ��Acharm�N�H�[�N�̎��ʂ� �Ƃ��āA
�Ƃ��āA (
( ���Ԏq�̃G�l���M�[)�ƂȂ��Ă���Aup�N�H�[�N�Adown�N�H�[�N�Astrange�N�H�[�N�ɐԐ�3��ނ�charm�N�H�[�N(�d��
���Ԏq�̃G�l���M�[)�ƂȂ��Ă���Aup�N�H�[�N�Adown�N�H�[�N�Astrange�N�H�[�N�ɐԐ�3��ނ�charm�N�H�[�N(�d�� )��������āA�n�h�����̔����f�ʐςɂ��āA
)��������āA�n�h�����̔����f�ʐςɂ��āA
 �C
�C
 ���Ԏq(
���Ԏq( )���������Ă��܂����B�܂��A�d�q�E�z�d�q�̃G�l���M�[������ɏグ�������̒�����A���v�g����1975�N�ї��q����������A��3����̃��v�g���ł���ї��q�A�уj���[�g���m�̑g���m�F����܂����B�������炳��ɍ��G�l���M�[�̗̈�ł́A
)���������Ă��܂����B�܂��A�d�q�E�z�d�q�̃G�l���M�[������ɏグ�������̒�����A���v�g����1975�N�ї��q����������A��3����̃��v�g���ł���ї��q�A�уj���[�g���m�̑g���m�F����܂����B�������炳��ɍ��G�l���M�[�̗̈�ł́A �̔�r����Ƀї��q������E�B�[�N�E�{�\��������蕡�G�ɂȂ�܂��B1977�N�ɂ́Abottom�N�H�[�N���\�����q�Ƃ��郲(�E�v�V����)���q����������A1995�N�ɁA����top�N�H�[�N���Atop�N�H�[�N�����Ăł����ƌ�����W�{�\����bottom�N�H�[�N�E�W�F�b�g���m�F����A���сE�v�엝�_��������܂����B
�̔�r����Ƀї��q������E�B�[�N�E�{�\��������蕡�G�ɂȂ�܂��B1977�N�ɂ́Abottom�N�H�[�N���\�����q�Ƃ��郲(�E�v�V����)���q����������A1995�N�ɁA����top�N�H�[�N���Atop�N�H�[�N�����Ăł����ƌ�����W�{�\����bottom�N�H�[�N�E�W�F�b�g���m�F����A���сE�v�엝�_��������܂����B
�N�H�[�N�̍ł�����ȕ������q�́A�z�q�ƒ����q�ł��B�z�q�̎����̑���̂��߂ɁA���_���̃X�[�p�[�E�J�~�I�J���f�ɂ����āA���N �̗z�q���ϑ�����Ă��܂����A���̂Ƃ����x���z�q����͊ϑ�����Ă��Ȃ��Ƃ̂��ƂŁA�z�q�̎�����
�̗z�q���ϑ�����Ă��܂����A���̂Ƃ����x���z�q����͊ϑ�����Ă��Ȃ��Ƃ̂��ƂŁA�z�q�̎����� �N�ȏ�Ƃ���Ă��܂��B�����q�͌��q�j���ł͋ɂ߂Ĉ���ł����A�j�O�ɏo�Ă��܂��ƕs����ɂȂ�A15����ŗz�q�Ɠd�q�Ɣ��d�q�j���[�g���m�Ƀ����Ă��܂��܂��B�����q�̎����́A���o����ŕ������𐔂�����@�ƁA�e����ɒ����q������߂Ă����c���������q���𐔂�����@�ƂŌ��ʂ��قȂ�A���̌�������Ƃ���Ă��܂��B���m�̑f���q�̒a���Ƃ����\�����l�����邻���ł��B
�N�ȏ�Ƃ���Ă��܂��B�����q�͌��q�j���ł͋ɂ߂Ĉ���ł����A�j�O�ɏo�Ă��܂��ƕs����ɂȂ�A15����ŗz�q�Ɠd�q�Ɣ��d�q�j���[�g���m�Ƀ����Ă��܂��܂��B�����q�̎����́A���o����ŕ������𐔂�����@�ƁA�e����ɒ����q������߂Ă����c���������q���𐔂�����@�ƂŌ��ʂ��قȂ�A���̌�������Ƃ���Ă��܂��B���m�̑f���q�̒a���Ƃ����\�����l�����邻���ł��B
�W�����_�ł́A�j���[�g���m�͎��ʂ������Ȃ��ƍl�����Ă��܂����B���ʂ������Ȃ����q�͌����ňړ����܂����A���ʂ������q�̑��x�͌����ɒB���邱�Ƃ͂���܂���B�j���[�g���m�͍������̃j���[�g���m�����������Ă��܂���B���j���[�g���m�͉E�����̂��̂����������Ă��܂���B���̂��߂ɁA�j���[�g���m�ɂ͎��ʂ��Ȃ��ƍl�����܂����B�������̃j���[�g���m�ɉ��Ɏ��ʂ�����Ƃ��āA���������x���Ƃ���ƁA�������̃j���[�g���m�����Ă����ϑ��҂��j���[�g���m���������X�s�[�h�ł��̃j���[�g���m��ǂ��z���U��Ԃ��ăj���[�g���m������ƉE�����Ɍ�����͂��ł����A�E�����̃j���[�g���m�͊ϑ�����Ă��܂���B����́A�j���[�g���m�������Ŕ�щ���Ă��Ď��ʂ������Ă��Ȃ��؋����A�Ƃ������ƂɂȂ��Ă��܂����B
��X�̎��͂ōő�̃j���[�g���m�������͑��z�ł��B���z�������j���[�g���m�z�j���[�g���m�ƌ����܂��B1960�N����A���z�j���[�g���m�̊ϑ����s���Ă��܂����A�{���\������Ă��鐔�� �̃j���[�g���m�����ϑ�����Ă��Ȃ��̂ł��B���̖��́u���z�j���[�g���m���v�ƌ����Č����҂�Y�܂��Ă��܂����B
�̃j���[�g���m�����ϑ�����Ă��Ȃ��̂ł��B���̖��́u���z�j���[�g���m���v�ƌ����Č����҂�Y�܂��Ă��܂����B
�܂��A�n���ɂ͉F��������j���[�g���m������Ă��܂��B1987�N�ɑ�}�[�������_�̒��ŋN�������V������(�n������16�����N�̂��Ȃ��Ȃ̂ŁA���ۂ̔������N�����̂�16���N�O�ł�)�Ŕ��������j���[�g���m�́A���̃J�~�I�J���f�ɂ����Ă�10�b���x�̊Ԃ�11��ϑ�����܂����B���V���̔������f������\�������l�ƈ�v������̂ł����B�܂��A�F���������Ă���l�X�ȉF�������n����C���̌��q�j�ƏՓ˂��āA�j���[�g���m�����܂��B�j���[�g���m�́A���̕����Ƃ̑��ݍ�p���������A�_����痈��ʃj���[�g���m�ƒn���̗������痈��ʃj���[�g���m�̐��͖{�������̂͂��ł����A�X�[�p�[�J�~�I�J���f�̊ϑ����ʂɂ��ƁA�����������Ă���ʃj���[�g���m�͗\���̔������x��������܂���ł����B�X�[�p�[�J�~�I�J���f�̊ϑ����ʂ���A1998�N�A���c���͂�́A�ʃj���[�g���m���n���̒��a���x�̋�����i�ފԂɃуj���[�g���m�ɓ]�����ăX�[�p�[�J�~�I�J���f�����蔲���Ă��܂��A�ƁA�������܂����B�j���[�g���m���ʎ�ɓ]�����錻�ۂ��A�ʂ��тɂȂ�����܂��ʂɖ߂����肷��̂��j���[�g���m�U���ƌ����܂�(�����_�ł́A�d�q�j���[�g���m���A�ʃj���[�g���m�E�уj���[�g���m�ɓ]�����錻�ۂ��m�F����Ă��܂�)�B����ɂ��A�]�����鎞�Ԃ����邱�Ƃ���j���[�g���m�̈ړ����x�͌��������A�Ƃ������ƂɂȂ�A�j���[�g���m�͎��ʂ������Ă���A�ƌ��_����܂����B
�����܂ŁA�f���q�����w�Ɍ����Ώ̐��ɂ��ĐF�X�����Ă��܂����B�ʎq�F�͊w�� �Ώ̐��A�d�����ݍ�p�Ǝア���ݍ�p��I�Ɉ������C���o�[�O�E�T�������_�ɂ�����
�Ώ̐��A�d�����ݍ�p�Ǝア���ݍ�p��I�Ɉ������C���o�[�O�E�T�������_�ɂ����� �Ώ̐��A���ɂ����ΐ����_�ɂ����郍�[�����c�s�ϐ��A�Q�[�W�ϊ��ɂ�����Q�[�W�s�ϐ��Ȃǂ��o�ꂵ�܂��B�������x���ł��A�Ε����˂̂悤�ȓ�����������Ƃ��ɁA�Ώ̐��𗘗p����Ƃ��܂�������ꍇ������܂��B���������Ώ̐��ƕۑ����Ƃ�I�ɍl����u�l�[�^�[�̒藝�v�Ƃ������w�̒藝������܂��B�h�C�c�̕s���̃��_���l�������w�҃G�~�[�E�l�[�^�[�ɂ���āA1915�N�ɏؖ�����1918�N�ɔ��\���ꂽ�藝�ł����A
�Ώ̐��A���ɂ����ΐ����_�ɂ����郍�[�����c�s�ϐ��A�Q�[�W�ϊ��ɂ�����Q�[�W�s�ϐ��Ȃǂ��o�ꂵ�܂��B�������x���ł��A�Ε����˂̂悤�ȓ�����������Ƃ��ɁA�Ώ̐��𗘗p����Ƃ��܂�������ꍇ������܂��B���������Ώ̐��ƕۑ����Ƃ�I�ɍl����u�l�[�^�[�̒藝�v�Ƃ������w�̒藝������܂��B�h�C�c�̕s���̃��_���l�������w�҃G�~�[�E�l�[�^�[�ɂ���āA1915�N�ɏؖ�����1918�N�ɔ��\���ꂽ�藝�ł����A
�Ώ̐��@�́@�ۑ���
�Ƃ������Ƃ��咣���Ă���藝�ł��B���̒藝�ɂ��ƁA
��ԕ��i�ɑ��ĕs�ςł���ƑS�^���ʂ��ۑ�����A��ԉ�]�ɑ��ĕs�ςł���ƑS�p�^���ʂ��ۑ�����A���Ԍo�߂ɑ��ĕs�ςł���ƑS�G�l���M�[���ۑ�����A�Q�[�W�ϊ��ɑ��ĕs�ςł���ƑS�d�ׂ��ۑ������A�Ƃ������Ƃ������܂��B��发�ł́A�l�[�^�[�̒藝�Ɋ�Â��đf���q�_�̑Ώ̐����o���Ă���̂��悭���܂��B
�Ō�ɁA�W���͌^�ɂ�����f���q�̕��ނɂ��Ă܂Ƃ߂Ă����܂��傤�B
(1) �Q�[�W�{�\�����F�f���q�Ԃɓ����͂�`�B����X�s��1�̗��q�B�{�[�Y���v�ɏ]���܂��B
���qγ�F�d���g�ƂȂ��ēd���I�ȗ͂�}������ȃQ�[�W���q�B���ʂ�0�ł��B
�O���[�I���F�N�H�[�N�Ԃ����������鋭���͂�`�B���闱�q�B�P�̂ł͌������Ă��܂���B�F�ׂ������A���ʂ�0�ł��B
�v�{�\���F�ア���ݍ�p�œ������q�ł��B�Q�[�W���q�ł����A�q�b�O�X�@�\�ɂ��傫�Ȏ��� �������A�ɂ߂ĒZ�����ł��B���d�ׂ�����
�������A�ɂ߂ĒZ�����ł��B���d�ׂ����� �C���d�ׂ�����
�C���d�ׂ����� ������܂��B������̉ߒ��ŁA
������܂��B������̉ߒ��ŁA  �C
�C
�̂悤�ɁA����܂��B
�y�{�\���G�ア���ݍ�p�œ������q�ł��B�Q�[�W���q�ł����A�q�b�O�X�@�\�ɂ��傫�Ȏ��� �������A�ɂ߂ĒZ�����ł��B�d�ׂ�0�ł��B�t�F���~���q�Ɣ��t�F���~���q�ɕ��܂��B
�������A�ɂ߂ĒZ�����ł��B�d�ׂ�0�ł��B�t�F���~���q�Ɣ��t�F���~���q�ɕ��܂��B (2) �q�b�O�X���q�F�q�b�O�X�@�\�ɂ��f���q�Ɏ��ʂ�^���闱�q�B
(3) ���v�g���F�������ݍ�p�Ɋ֗^���Ȃ��X�s�� �̌y���q�B�t�F���~���v�ɏ]���܂��B�N�H�[�N�A���v�g���̎�ނ��t���[�o�[�ƌ����܂��B
�̌y���q�B�t�F���~���v�ɏ]���܂��B�N�H�[�N�A���v�g���̎�ނ��t���[�o�[�ƌ����܂��B �E��1����
�d�qe�F�ɂ߂Ĉ���ŁA�d�� �������܂��B���ʂ́A
�������܂��B���ʂ́A �B���d��
�B���d�� �����z�d�q
�����z�d�q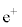 �͔����q�B
�͔����q�B �d�q�j���[�g���m �F����ȗ��q�œd��0�D���ʂ�
�F����ȗ��q�œd��0�D���ʂ� ���x�ȉ��ł��B
���x�ȉ��ł��B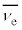 �͔����q�B
�͔����q�B �E��2����
�ʗ��q(�~���[�I��)�F�d�q�ɂ悭���Ă���d�� �̗��q�C���ʂ́A
�̗��q�C���ʂ́A �B���d��
�B���d�� ������
������ �͔����q�B����
�͔����q�B���� �ŁA
�ŁA �ƕ��܂��B
�ʃj���[�g���m �F�d��0�̈���ȗ��q�B���ʂ͋ɂ߂ď������B
�F�d��0�̈���ȗ��q�B���ʂ͋ɂ߂ď������B �͔����q�B
�͔����q�B �E��3����
�ї��q(�^�E�I��)�F�d���_�������A�d�q�ɂ悭���Ă���d�� �̗��q�C���ʂ́A
�̗��q�C���ʂ́A �B���d��
�B���d�� ������
������ �͔����q�B����
�͔����q�B���� �ŁA
�ŁA �Ȃǂƕ��܂��B�Ȃ��A
�ȂǂƁA�n�h�����ɂ����܂��B
�уj���[�g���m �F�d��0�̈���ȗ��q�B���ʂ͋ɂ߂ď������B
�F�d��0�̈���ȗ��q�B���ʂ͋ɂ߂ď������B (4) �N�H�[�N�F�z�q�A�����q�A�Β��Ԏq�̂悤�ȃn�h�������\������X�s��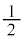 �̗��q�Ńt�F���~���v�ɏ]���܂��B�O���[�I���ɂ�鋭���͂Ō������Ă���A�P�̂ł͔�������Ă��܂���B�F��(�X�I�ɁA�ԁA�A��3�ʂ�)�������A�F�ׂ̍��������ɂȂ�悤�ɁA2�A���邢�́A3�̑g�Ńn�h����(2�Œ��Ԏq�A3�Ńo���I��)���\�����܂��B�����p�ɂ́A(4)�̐����Ɗe�N�H�[�N�̓d�ׂ��L�����Ă��������B
�̗��q�Ńt�F���~���v�ɏ]���܂��B�O���[�I���ɂ�鋭���͂Ō������Ă���A�P�̂ł͔�������Ă��܂���B�F��(�X�I�ɁA�ԁA�A��3�ʂ�)�������A�F�ׂ̍��������ɂȂ�悤�ɁA2�A���邢�́A3�̑g�Ńn�h����(2�Œ��Ԏq�A3�Ńo���I��)���\�����܂��B�����p�ɂ́A(4)�̐����Ɗe�N�H�[�N�̓d�ׂ��L�����Ă��������B �E��1����
up�N�H�[�N(u)�F ���x�̎��ʂ�������ȗ��q�ŁA�d��
���x�̎��ʂ�������ȗ��q�ŁA�d�� �������܂��B�����q��
�������܂��B�����q�� �͓d��
�͓d�� �������܂��B
�������܂��B down�N�H�[�N(d)�F ���x�̎��ʂ�������ȗ��q�ŁA�d��
���x�̎��ʂ�������ȗ��q�ŁA�d�� �������܂��B�����q��
�������܂��B�����q�� �͓d��
�͓d�� �������܂��B��������down�N�H�[�N�̓�����ɂ��A
�������܂��B��������down�N�H�[�N�̓�����ɂ��A �ƕ��܂�(���̔����͊o���Ă�������)�B
�E��2����
charm�N�H�[�N(c)�F ���x�̎��ʂ����s����ȗ��q�ŁA�d��
���x�̎��ʂ����s����ȗ��q�ŁA�d�� �������܂��B
�������܂��B strange�N�H�[�N(s)�F ���x�̎��ʂ����s����ȗ��q�ŁA�d��
���x�̎��ʂ����s����ȗ��q�ŁA�d�� �������܂��B
�������܂��B �E��3����
top�N�H�[�N(t)�F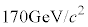 ���x�̎��ʂ������q�ŁA�d��
���x�̎��ʂ������q�ŁA�d�� �������܂��B�������ݍ�p���������Ԃ����������Z���A�n�h�������\���ł��܂���B
�������܂��B�������ݍ�p���������Ԃ����������Z���A�n�h�������\���ł��܂���B bottom�N�H�[�N(b)�F ���x�̎��ʂ����s����ȗ��q�ŁA�d��
���x�̎��ʂ����s����ȗ��q�ŁA�d�� �������܂��B
�������܂��B (5) �n�h�����F2�̃N�H�[�N����\������A�����X�s���̃{�[�Y���q�ł��钆�Ԏq(���\��)�ƁA3�̃N�H�[�N����\������A�������X�s���̃t�F���~���q�ł���o���I��������B
�E���Ԏq(���\��)
�Β��Ԏq�F����G�����\���������q�ŁA�j�q�Ԃɓ����j�͂�}��܂��B�X�g�����W�l�X0�ł��B���� �ŁA���d�ׂ�L����
�ŁA���d�ׂ�L���� (
( )�C���d�ׂ�L����
)�C���d�ׂ�L���� (
( )�C����
)�C���� �œd�ׂ������Ȃ�
�œd�ׂ������Ȃ� (
( )������A
)������A �C
�C �́A����
�́A���� �ŁA
�ŁA  �C
�C
�̂悤�ɕ��܂��B �́A����
�́A���� �ŁA
�ŁA �̂悤�ɕ��܂��B
K���Ԏq�F���� �ŁA�X�g�����W�l�X1�Ő��d�ׂ�L����
�ŁA�X�g�����W�l�X1�Ő��d�ׂ�L���� (
( )�C�X�g�����W�l�X
)�C�X�g�����W�l�X �ŕ��d�ׂ�L����
�ŕ��d�ׂ�L���� (
( )�́A����
)�́A���� �ł����A
�ł����A �͊���̕���p�^�[��������A
�͊���̕���p�^�[��������A  (64��)
(64��)
 (21��)
(21��)
 (6��)
(6��)
 (5��)
(5��)
 (2��)
(2��)�̂悤�ɕ��܂��B���ɁA�d�ׂ������Ȃ����� �C�X�g�����W�l�X1��
�C�X�g�����W�l�X1�� (
( )�ƁA���̔����q�ŃX�g�����W�l�X
)�ƁA���̔����q�ŃX�g�����W�l�X ��
�� (
( )������A
)������A �ɂ́A
�ɂ́A ��
�� �̍����ł��钷������
�̍����ł��钷������ (
( )�ƒZ������
)�ƒZ������ (
( )������(�������������O��
)������(�������������O�� �������̂�
�������̂� �������̂��A�����������Ȃ��̂ō������l����)�A
�������̂��A�����������Ȃ��̂ō������l����)�A �̂悤�ɕ��܂�(���̕���̍ۂ�CP�Ώ̐����j��܂�)�B
����ɒ��Ԏq�ɂ͑��ɁA�X�s��0�� �C�X�s��1��
�C�X�s��1�� �C
�C �C
�C �C
�C �C
�C �C��
�C�� �Ȃǂ�����܂��B
�Ȃǂ�����܂��B �E�o���I���F�����p�ɂ́A�z�q�A�����q�̃N�H�[�N�̍\�����L�����܂��傤�B
�z�q(p)�F�N�H�[�Nuud�̑g�ݍ��킹�œd�� �����ɂ߂Ĉ���ȗ��q�ł��B�X�g�����W�l�X��0�C���ʂ́A
�����ɂ߂Ĉ���ȗ��q�ł��B�X�g�����W�l�X��0�C���ʂ́A �B
�B �́A���d��
�́A���d�� �������z�q�ł��B
�������z�q�ł��B �����q(n)�F�N�H�[�Nudd�̑g�ݍ��킹�œd�ׂ������Ȃ����q�ł��B�X�g�����W�l�X0�C���ʂ� �ł��B���q�j���ł͈���ł����A�P�Ƃł͖�
�ł��B���q�j���ł͈���ł����A�P�Ƃł͖� �Ń�����(�ア���ݍ�p)���āA
�Ń�����(�ア���ݍ�p)���āA �ƂȂ�܂��B
�����q�F�N�H�[�Nuds�̑g�ݍ��킹�œd�ׂ������Ȃ��X�g�����W�l�X �̗��q�B����
�̗��q�B���� �ł����A����
�ł����A���� �ŁA
�ŁA �̂悤�Ɏア���ݍ�p�ŕ��܂��B
�����q�F�d�� ��
�� (uus)�́A����
(uus)�́A���� �C����
�C���� �ŁA
�ŁA �̂悤�Ɏア���ݍ�p�ŕ��܂��B���ɁA�d�� �C����
�C���� �C����
�C���� ��
��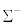 (dds)�C�d�ׂ������Ȃ�����
(dds)�C�d�ׂ������Ȃ����� ��
�� (uds)������܂����A
(uds)������܂����A �͎���
�͎���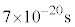 �Ń����āA
�Ń����āA �ƂȂ�܂��B �C
�C �C
�C ��������X�g�����W�l�X��
��������X�g�����W�l�X�� �ł��B
�ł��B �����q�F�d�� ��
�� (dss)�́A����
(dss)�́A���� �C����
�C���� �ŁA
�ŁA �̂悤�Ɏア���ݍ�p�ŕ��܂��B�d�ׂ������Ȃ� (uss)�́A����
(uss)�́A���� �C����
�C���� �ŁA
�ŁA �̂悤�Ɏア���ݍ�p�ŕ��܂��B �C
�C �Ƃ��ɃX�g�����W�l�X
�Ƃ��ɃX�g�����W�l�X �ł��B
�ł��B �����q�F�N�H�[�Nsss�̍\���ŁA���� �C�d��
�C�d�� �����X�g�����W�l�X
�����X�g�����W�l�X �̗��q�ŁA���̗��q�̓X�s��
�̗��q�ŁA���̗��q�̓X�s�� �ł��B����
�ł��B���� �ŁA
�ŁA �̂悤�Ɏア���ݍ�p�ŕ��܂��B
�����q�F�d�� ��
�� (uuu)�C�d��
(uuu)�C�d�� ��
�� (uud)�C�d��0��
(uud)�C�d��0�� (udd)�C�d��
(udd)�C�d�� ��
�� (ddd)������܂��B��������A���ʂ�
(ddd)������܂��B��������A���ʂ�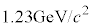 �C����
�C���� (�j�q�ƃΒ��Ԏq�ɕ��܂�)�ŁA�X�g�����W�l�X��0�C�X�s��
(�j�q�ƃΒ��Ԏq�ɕ��܂�)�ŁA�X�g�����W�l�X��0�C�X�s�� �̗��q�ł�(�����q���N�H�[�N�̍\����udd�ł����A�X�s����3�̂���1���t�����A
�̗��q�ł�(�����q���N�H�[�N�̍\����udd�ł����A�X�s����3�̂���1���t�����A �ł�3�Ƃ��������)�B
�ł�3�Ƃ��������)�B
138���N�O�A�r�b�O�o���ɂ���Ēa�������������̉F���ł͈͗͂�ł����B��������A4�̗́A�d�́A�d���́A�����́A�ア�͂ɕ�����A�F�����₦�ăq�b�O�X�@�\�ɂ�莿�ʂ��ł��܂����B���݁A�F���̕����̂����A�W�����_�Ő��������̂�5�������ŁA�_�[�N�}�^�[��������ł��Ă��邩����ł��B�j���[�g���m�U���A���邢�́A��4����ȍ~�̃N�H�[�N�E���v�g���͑��݂���̂�(��4����j���[�g���m�́A���݂���Ƃ��Ă�����Ȏ��ʂ̂͂��ŁA���̊m���͂��Ȃ菬���������ł�)�A�P�̃g�b�v�E�N�H�[�N�ȂǁA�W�����_�Ő����̂��Ȃ����ۂ��������Ă��܂��B
���݁ASU(3)�~SU(2)�~U(1)�Ώ̐�������ɓ����I�ɑ�����SU(5)�Ώ̐��ɂ��哝�ꗝ�_������Ă��܂��B�����w�����ꂩ�猩�����悤�Ȍ����_�̒�����Ȃ���Ă��܂��B�f���q�_�́A�~�N���ȕ������������̕�����1����Ƃ����̂łȂ��A�ߎ���ۓ��₻�̑��̌v�Z�Z�I���܂߂āA�F���̐��藧���܂ł��ΏۂƂ��镨���w�S�̂��I�Ɉ������_�ɂȂ��Ă��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �̂悤�ɕ\����܂��B�N�H�[�N�ƃ��v�g���̂����A�������̂��̂�
�̂悤�ɕ\����܂��B�N�H�[�N�ƃ��v�g���̂����A�������̂��̂� �Ƃ��āA�Î~�G�l���M�[���������q�b�O�X�E�|�e���V�����G�l���M�[(�O���t�ɕ`�����`�烁�L�V�J���E�n�b�g�E�|�e���V�����ƌĂ�܂�)�A
�Ƃ��āA�Î~�G�l���M�[���������q�b�O�X�E�|�e���V�����G�l���M�[(�O���t�ɕ`�����`�烁�L�V�J���E�n�b�g�E�|�e���V�����ƌĂ�܂�)�A �ɂ�����V���ɏ��l�����A����Ȃ荇���̈ʒu���ω����܂��B
�ɂ�����V���ɏ��l�����A����Ȃ荇���̈ʒu���ω����܂��B �Ƃ����āA������^����Ғl�ƌ����܂��B�܂�A�^��́A�G�l���M�[���[���̏�Ԃɂ���̂ł͂Ȃ��A�L���̊��Ғl������ϕ����Ԃɖ����Ă���Ƃ����̂ł��B
�Ƃ����āA������^����Ғl�ƌ����܂��B�܂�A�^��́A�G�l���M�[���[���̏�Ԃɂ���̂ł͂Ȃ��A�L���̊��Ғl������ϕ����Ԃɖ����Ă���Ƃ����̂ł��B
 �C
�C

 �C�X�s��1��
�C�X�s��1�� �C
�C