�f���q(����2)����̂Â��ł��B
1898�N�A���U�t�H�[�h�ɂ���Ĕ������ꂽ������ł́A���q�j���ŁA
�Ƃ����������N���܂����A�����́A�j���[�g���m ���d�C�I�ɒ����Ŗ����ɔ�Ղ��c�����A���̔������m���Ă��܂���ł����B���̂��߁A��������
���d�C�I�ɒ����Ŗ����ɔ�Ղ��c�����A���̔������m���Ă��܂���ł����B���̂��߁A�������� ���Ȃ��ƁA�����q
���Ȃ��ƁA�����q �̎��ʂƗz�q
�̎��ʂƗz�q �Ɠd�q
�Ɠd�q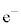 �̎��ʂ̍�����яo���Ă���d�q
�̎��ʂ̍�����яo���Ă���d�q �̉^���G�l���M�[�ƈ�v���Ȃ��Ȃ�̂ŁA�G�l���M�[�ۑ������藧���Ȃ��̂ł͂Ȃ����A�ƌ����Ă��܂����B�������d�q�̃G�l���M�[�E�X�y�N�g�������X�y�N�g���łȂ��A���X�y�N�g���ł����B�܂��A�����q�̃X�s����
�̉^���G�l���M�[�ƈ�v���Ȃ��Ȃ�̂ŁA�G�l���M�[�ۑ������藧���Ȃ��̂ł͂Ȃ����A�ƌ����Ă��܂����B�������d�q�̃G�l���M�[�E�X�y�N�g�������X�y�N�g���łȂ��A���X�y�N�g���ł����B�܂��A�����q�̃X�s���� �C������̗z�q�A�d�q�̃X�s����
�C������̗z�q�A�d�q�̃X�s���� �̂����ꂩ�ŁA�����ŃX�s�����ۑ����܂���B1930�N�X�C�X�̃p�E���́A������ɂ����Ă��G�l���M�[�ۑ��A�X�s���̕ۑ��𐬗������邽�߂ɁA�X�s��
�̂����ꂩ�ŁA�����ŃX�s�����ۑ����܂���B1930�N�X�C�X�̃p�E���́A������ɂ����Ă��G�l���M�[�ۑ��A�X�s���̕ۑ��𐬗������邽�߂ɁA�X�s�� �C�d�C�I�ɒ����Ȗ��m�̗��q����яo���Ă���Ƃ�����������܂����B1934�N�C�^���A�̃t�F���~�����m�̗��q���j���[�g���m�ƌĂсA�j���[�g���m���܂߂�������̗��_�\���܂����B�t�F���~�́A������̌����萔���A�������ݍ�p�̌����萔�Ɣ�ׂĔ��ɏ������A������̉ߒ����ア���ݍ�p�ƌĂт܂����B�j���[�g���m�͎��ʂ�0�������͔��ɏ��������o�̓�����q�ŁA1950�N��ɓ���A�č��̃��C�l�X�ƃJ���������q�F���甭������j���[�g���m�Ɛ��Ƃ̔������ϑ����邱�Ƃɂ�葶�݂��ؖ�����܂����B
�C�d�C�I�ɒ����Ȗ��m�̗��q����яo���Ă���Ƃ�����������܂����B1934�N�C�^���A�̃t�F���~�����m�̗��q���j���[�g���m�ƌĂсA�j���[�g���m���܂߂�������̗��_�\���܂����B�t�F���~�́A������̌����萔���A�������ݍ�p�̌����萔�Ɣ�ׂĔ��ɏ������A������̉ߒ����ア���ݍ�p�ƌĂт܂����B�j���[�g���m�͎��ʂ�0�������͔��ɏ��������o�̓�����q�ŁA1950�N��ɓ���A�č��̃��C�l�X�ƃJ���������q�F���甭������j���[�g���m�Ɛ��Ƃ̔������ϑ����邱�Ƃɂ�葶�݂��ؖ�����܂����B
1947�N�A�F�����̑��ݍ�p�̒�����K���Ԏq�ƃ����q����������܂����B�d�ׂ������Ȃ� ��
�� �́A���̉ߒ��Ő�������܂��B
�́A���̉ߒ��Ő�������܂��B
 �@����@
�@����@ �́A�j�q����ʉ߂���
�́A�j�q����ʉ߂��� ���x�̎��Ԃ̊Ԃɗz�q�ƏՓ˂�
���x�̎��Ԃ̊Ԃɗz�q�ƏՓ˂� ���x�̎��Ԃ�
���x�̎��Ԃ� ��
�� �����܂��B�Ƃ��낪�A
�����܂��B�Ƃ��낪�A �͐������Ԃ������Ȃ蒷��
�͐������Ԃ������Ȃ蒷�� ���x�̎��ԂŁA
���x�̎��ԂŁA
 �@����A
�@����A ���v�Z���
���v�Z��� ���x�̎��������͂��ł������A
���x�̎��������͂��ł������A �Ƃ�����r�I�������ԂŁA
�Ƃ�����r�I�������ԂŁA
 �@����B
�@����B ��
�� ���������ݍ�p������̂Ńn�h�����ł����A�������Ԃƕ��Ԃ̔䂪1�F
���������ݍ�p������̂Ńn�h�����ł����A�������Ԃƕ��Ԃ̔䂪1�F �Ƃ��܂�ɑ傫���Astrange particles�ƌĂ�܂����B1953�N�A����O�v�A�����a�F�A�č��̃Q���}���́A�f���q���X�g�����W�l�XS�Ƃ����ʎq���������Ă��āA�������ݍ�p�ł́A�X�g�����W�l�XS���ۑ�����锽��������������A�A�C�B�̓n�h�������m�̔����ł����Ă��������ݍ�p�ł͂Ȃ��A���̂��߂�
�Ƃ��܂�ɑ傫���Astrange particles�ƌĂ�܂����B1953�N�A����O�v�A�����a�F�A�č��̃Q���}���́A�f���q���X�g�����W�l�XS�Ƃ����ʎq���������Ă��āA�������ݍ�p�ł́A�X�g�����W�l�XS���ۑ�����锽��������������A�A�C�B�̓n�h�������m�̔����ł����Ă��������ݍ�p�ł͂Ȃ��A���̂��߂� ��
�� ��(�f���q�Ƃ��Ă�)�������������̂��A�Ǝ咣���܂����B�@�̔����́A
��(�f���q�Ƃ��Ă�)�������������̂��A�Ǝ咣���܂����B�@�̔����́A ��
�� ��
�� �C
�C ��
�� �C
�C ��
�� �C�X�g�����W�l�XS���ۑ������̂ŋ������ݍ�p�ł����A�A�C�B�̔����́A
�C�X�g�����W�l�XS���ۑ������̂ŋ������ݍ�p�ł����A�A�C�B�̔����́A ��
�� �ŁA�ǂ�����X�g�����W�l�X��1�ω����Ă��邽�߁A�ア���ݍ�p�ɂ���ċN����A�ƍl����ꂽ�̂ł��BK���Ԏq�́A
�ŁA�ǂ�����X�g�����W�l�X��1�ω����Ă��邽�߁A�ア���ݍ�p�ɂ���ċN����A�ƍl����ꂽ�̂ł��BK���Ԏq�́A ������
������ �C�d�ׂ�����
�C�d�ׂ����� ��
�� ������
������ �Ŋj�q���͏��������ʂł����A
�Ŋj�q���͏��������ʂł����A �͎���
�͎��� �ŁA�z�q�̎���
�ŁA�z�q�̎���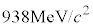 �C�����q�̎���
�C�����q�̎��� �Ɠ����x�̏d�����q�ł��B�z�q�A�����q�A�����q�́A�o���I��(�d���q)�ƌĂ�A�o���I����1�Ƃ���܂��BK���Ԏq�A�Β��Ԏq�͔�r�I�y���o���I����0�ł��B�d�C�f�ʂ�P�ʂƂ���d�ׂ�Q�C�o���I������B�C�X�g�����W�l�X��S�C�A�C�\�X�s����
�Ɠ����x�̏d�����q�ł��B�z�q�A�����q�A�����q�́A�o���I��(�d���q)�ƌĂ�A�o���I����1�Ƃ���܂��BK���Ԏq�A�Β��Ԏq�͔�r�I�y���o���I����0�ł��B�d�C�f�ʂ�P�ʂƂ���d�ׂ�Q�C�o���I������B�C�X�g�����W�l�X��S�C�A�C�\�X�s���� �Ƃ��āA
�Ƃ��āA
�Ƃ����W������܂��B�����ŁA �����d���ƌ����܂��BK���Ԏq�⃩���q���n�h�����ɕ���Ƃ��A�ア���ݍ�p�̏ꍇ�ɂ́A�X�g�����W�l�XS���ۑ����Ȃ��̂ŁA�A�C�\�X�s��
�����d���ƌ����܂��BK���Ԏq�⃩���q���n�h�����ɕ���Ƃ��A�ア���ݍ�p�̏ꍇ�ɂ́A�X�g�����W�l�XS���ۑ����Ȃ��̂ŁA�A�C�\�X�s�� �C���d��Y���ۑ����܂���B
�C���d��Y���ۑ����܂���B
�����ŁA�Q�[�W�ϊ��ƑΏ̐��ɂ��ĐG��Ă����܂��B�}�N�X�E�F���̕����������d��������߂�Ƃ��A�^�ŁA �C
�C �Ƃ��āA
�Ƃ��āA
 �@����C
�@����C ��
�� �����߂�Ηǂ��̂ł����A
�����߂�Ηǂ��̂ł����A (
( ���x�N�g���E�|�e���V�����ƌ����܂�)�Ƃ����ƇC��4�Ԗڂ̎��́A
���x�N�g���E�|�e���V�����ƌ����܂�)�Ƃ����ƇC��4�Ԗڂ̎��́A

 �Ȃ̂ŁA
�Ȃ̂ŁA �Ƃ������Ƃ��ł��܂��B������A
�Ƃ������Ƃ��ł��܂��B������A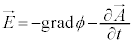
 ��ϕ�����߁A
��ϕ�����߁A �C
�C �����߂�Ηǂ��̂ł����A
�����߂�Ηǂ��̂ł����A
 �C
�C �@����D
�@����D
 �C
�C
 �C
�C ���A
���A
 �C
�C
 �C
�C �Ɠ������������܂��B�}�N�X�E�F���̕������͇D�̕ϊ��ɑ��ĕs�ςȂ̂ł��B�D���Q�[�W�ϊ��ƌ����܂��B�D�̃Q�[�W�ϊ��́A���Θ_�I�ȏ�����������ƁA
�Ɠ������������܂��B�}�N�X�E�F���̕������͇D�̕ϊ��ɑ��ĕs�ςȂ̂ł��B�D���Q�[�W�ϊ��ƌ����܂��B�D�̃Q�[�W�ϊ��́A���Θ_�I�ȏ�����������ƁA ���0����
���0���� �C
�C ��
�� �C
�C �C
�C �����Ƃ���4���x�N�g��
�����Ƃ���4���x�N�g�� ���g���āA
���g���āA �Ə����A
�Ə����A �ƂȂ�܂��B�f�B���b�N������
�ƂȂ�܂��B�f�B���b�N������
 �@����E
�@����E �Ƃ����ϊ����s���Ă����藧���܂��B���̕ϊ��́A
�Ƃ����ϊ����s���Ă����藧���܂��B���̕ϊ��́A �̂悤�ɏ�����Ƃ��A
�̂悤�ɏ�����Ƃ��A �̂悤�Ɉʑ���δ�������炷���Ƃɑ������A����̊e�_����l�ɓ����ϊ�����̂ŁA��ǓI�ϊ�(�O���[�o���ϊ�)�ƌ����܂��B�܂��A
�̂悤�Ɉʑ���δ�������炷���Ƃɑ������A����̊e�_����l�ɓ����ϊ�����̂ŁA��ǓI�ϊ�(�O���[�o���ϊ�)�ƌ����܂��B�܂��A �S�̂�1�������j�^���Q
�S�̂�1�������j�^���Q �����܂��B
�����܂��B
����ɑ��āA���̈ʑ��̂���δ����Ԃ̊e�_�ňقȂ�A�ʒux�̊� �ɂȂ�Ƃ��܂��B���̂Ƃ��A
�ɂȂ�Ƃ��܂��B���̂Ƃ��A �Ƃ����ϊ�(�Ǐ��I�ϊ��ƌ����܂�)���s���ƁA�f�B���b�N�������E�́A
�Ƃ����ϊ�(�Ǐ��I�ϊ��ƌ����܂�)���s���ƁA�f�B���b�N�������E�́A
�ƂȂ��āA�]�v�ȍ� ������A���̂��߂ɁA�f�B���b�N�������E���������Ȃ��Ȃ��Ă��܂��܂��B�����ŁA�d��q�Ƃ��A�x�N�g����
������A���̂��߂ɁA�f�B���b�N�������E���������Ȃ��Ȃ��Ă��܂��܂��B�����ŁA�d��q�Ƃ��A�x�N�g���� �����āA�f�B���b�N��������
�����āA�f�B���b�N�������� �����ϔ����F
�����ϔ����F �Œu������(���ϔ����Ƃ����l�����́A�V�����[�f�B���K�[���d���ꒆ�̉דd���q�ɑ���V�����[�f�B���K�[�������œ������Ă������̂ł�)�A
�Œu������(���ϔ����Ƃ����l�����́A�V�����[�f�B���K�[���d���ꒆ�̉דd���q�ɑ���V�����[�f�B���K�[�������œ������Ă������̂ł�)�A
�Ƃ����`�ŁA�Q�[�W�ϊ��̉e�����Ȃ��f�B���b�N���������l���܂��B���̈Ӗ��ŁA�Ǐ��I�ϊ����Q�[�W�ϊ��A ���Q�[�W���ƌ����܂��B���̂Ƃ����A
���Q�[�W���ƌ����܂��B���̂Ƃ����A �S�̂�1�������j�^���Q
�S�̂�1�������j�^���Q �����܂��B�Q�[�W��ɂ��A�דd���q�Ԃɓ����́A���̗͂�}��闱�q������܂��B�A���A�}�N�X�E�F���̕������ɁA
�����܂��B�Q�[�W��ɂ��A�דd���q�Ԃɓ����́A���̗͂�}��闱�q������܂��B�A���A�}�N�X�E�F���̕������ɁA �Ƃ���
�Ƃ��� �Ƃ����悤�Ȏ��ʍ������Ă��܂��ƁA
�Ƃ����悤�Ȏ��ʍ������Ă��܂��ƁA �Ƃ��āA
�Ƃ��āA
�ƂȂ�A�Q�[�W�Ώ̐������Ă��܂��̂ŁA�Q�[�W���q(���q)�͎��ʂ������Ƃ��ł��܂���(��ɁA �̃N���C���E�S���h�����������d���g�̕������ɂȂ邱�Ƃɂ��G��܂����B�f���q(����2)���Q��)�B
�̃N���C���E�S���h�����������d���g�̕������ɂȂ邱�Ƃɂ��G��܂����B�f���q(����2)���Q��)�B
1954�N�A�����ƃ~���Y�́A�z�q�E�����q�̃A�C�\�X�s�� �ɑ��āA2�s2��̃��j�^���s��U�ŕ\�����Q�[�W�ϊ�����p������
�ɑ��āA2�s2��̃��j�^���s��U�ŕ\�����Q�[�W�ϊ�����p������ �̕ϊ��ɑ���
�̕ϊ��ɑ��� �Ώ̐��ɏ]�����_�����܂����B
�Ώ̐��ɏ]�����_�����܂����B �ɑ�����s��̐ς͔���Ȃ̂ŁA����Q�[�W���_�ł��B�����E�~���Y�Ƃ͓Ɨ��ɓ��R���Y����ʑ��ΐ����_�������Q�[�W���_�����݂��Ă���A������ɂ���N�ȏ�x��Ĕ��\�����̂ł����A�ނ���A�����E�~���Y���_����ʑ��ΐ����_�������Ƃ̊m�F�ɂȂ�܂����B�����E�~���Y���_�́A�z�q�E�����q�̎��ʍ���d����̑Ώ̐��̔j��ɂ���Đ������悤�Ƃ����̂ł����A�������ʂƍ����܂���ł����B�ł����A���̗��_�́A���C���o�[�O�E�T�����̓d�㓝��
�ɑ�����s��̐ς͔���Ȃ̂ŁA����Q�[�W���_�ł��B�����E�~���Y�Ƃ͓Ɨ��ɓ��R���Y����ʑ��ΐ����_�������Q�[�W���_�����݂��Ă���A������ɂ���N�ȏ�x��Ĕ��\�����̂ł����A�ނ���A�����E�~���Y���_����ʑ��ΐ����_�������Ƃ̊m�F�ɂȂ�܂����B�����E�~���Y���_�́A�z�q�E�����q�̎��ʍ���d����̑Ώ̐��̔j��ɂ���Đ������悤�Ƃ����̂ł����A�������ʂƍ����܂���ł����B�ł����A���̗��_�́A���C���o�[�O�E�T�����̓d�㓝�� ���_�A�N�H�[�N�E�O���[�I�����L�q����
���_�A�N�H�[�N�E�O���[�I�����L�q���� �̗ʎq�F�͊w�ɂ��Ȃ���܂����B
�̗ʎq�F�͊w�ɂ��Ȃ���܂����B
�O�q�̃X�g�����W�l�X���ۑ����Ȃ�K���Ԏq�̕����A
 �@����F
�@����F
 �@����G
�@����G �ɈႢ���Ȃ����Ƃ������Ă��܂����B1956�N�A���[�ƃ����́A�ア���ݍ�p�ł̃p���e�B�[�ۑ���������Ă��Ȃ����Ƃ���A���҂͓��ꗱ�q�̕���ŁA���̔����ł̓p���e�B�[���ۑ����Ă��Ȃ��A�Ǝ咣���܂����B���N�A�E�[���A
�ɈႢ���Ȃ����Ƃ������Ă��܂����B1956�N�A���[�ƃ����́A�ア���ݍ�p�ł̃p���e�B�[�ۑ���������Ă��Ȃ����Ƃ���A���҂͓��ꗱ�q�̕���ŁA���̔����ł̓p���e�B�[���ۑ����Ă��Ȃ��A�Ǝ咣���܂����B���N�A�E�[���A
�Ƃ���������ŁA�ɒቷ�ɒu�����Ƃɂ��A �̃X�s���̌����𑵂��Ď������s�����Ƃ���A�㉺�ϓ��ɏo��͂��̓d�q�����A
�̃X�s���̌����𑵂��Ď������s�����Ƃ���A�㉺�ϓ��ɏo��͂��̓d�q�����A �̃X�s���Ƌt�����ɏo�Ă�����̂̕��������A�Ƃ����������ʂ������A�������痂�N�A�E�[�́A������ł̓p���e�B�[�ۑ�(��Ԕ��]�Ώ̐�)���j��Ă���A�ƌ��_���܂����B�]���āA�ア���ݍ�p�̑Ώ̐���
�̃X�s���Ƌt�����ɏo�Ă�����̂̕��������A�Ƃ����������ʂ������A�������痂�N�A�E�[�́A������ł̓p���e�B�[�ۑ�(��Ԕ��]�Ώ̐�)���j��Ă���A�ƌ��_���܂����B�]���āA�ア���ݍ�p�̑Ώ̐��� �ł͂Ȃ��A��]�Ώ̐���
�ł͂Ȃ��A��]�Ώ̐��� �ł��B�܂��A�{���A���q�Ɣ����q�Ƃ͓������ł���͂��Ȃ̂ɁA��X�̉F���ɂ͂قƂ�ǔ����q������܂���B�����A�����q���������݂��Ă���Η��q�ƌ������Č��q�ɂȂ��Ă��܂��A���̉F�������݂ł��Ȃ������m��܂���B���̉F�������R�Ƃ��đ��݂��Ă���A�Ƃ������Ƃ́A�F�����ł����Ƃ��ɉ��炩�̕肪�����Ă����A�Ƃ������Ƃ����m��܂���B
�ł��B�܂��A�{���A���q�Ɣ����q�Ƃ͓������ł���͂��Ȃ̂ɁA��X�̉F���ɂ͂قƂ�ǔ����q������܂���B�����A�����q���������݂��Ă���Η��q�ƌ������Č��q�ɂȂ��Ă��܂��A���̉F�������݂ł��Ȃ������m��܂���B���̉F�������R�Ƃ��đ��݂��Ă���A�Ƃ������Ƃ́A�F�����ł����Ƃ��ɉ��炩�̕肪�����Ă����A�Ƃ������Ƃ����m��܂���B
�ϊ��ƑΏ̐��̘b�ɖ߂�܂����A �C
�C (I�F�P�ʍs��)�Ƃ��āA�s��X�̎w����
(I�F�P�ʍs��)�Ƃ��āA�s��X�̎w���� ��(�}�N���[�����W�J���Q��)
��(�}�N���[�����W�J���Q��)
�ƒ�`����ƁA���f���𐬕��Ƃ���N���̃��j�^���s��U ( �C
�C )�́A�G���~�[�g�s��X (
)�́A�G���~�[�g�s��X ( )��p���āA
)��p���āA �ƕ\����邱�Ƃ��m���Ă��܂��B������m���߂Ă݂܂��B
�ƕ\����邱�Ƃ��m���Ă��܂��B������m���߂Ă݂܂��B
 ���A
���A
����āA
�����A �̓��j�^���s��ł��BV�CD�CX��N�������s��Ƃ��āA�G���~�[�g�s��̓��j�^���s��V�ɂ���đΊp���\�Ȃ̂ŁA
�̓��j�^���s��ł��BV�CD�CX��N�������s��Ƃ��āA�G���~�[�g�s��̓��j�^���s��V�ɂ���đΊp���\�Ȃ̂ŁA �Ƃ��āA
�Ƃ��āA �C
�C
����āA �̍s�́A
�̍s�́A
 �ɑ����郆�j�^���s��̍s��1�Ȃ̂ŁA
�ɑ����郆�j�^���s��̍s��1�Ȃ̂ŁA �Ƃ���ƁA
�Ƃ���ƁA
����āA �́AN���̃G���~�[�g�s��őΊp�a
�́AN���̃G���~�[�g�s��őΊp�a ���[���ɂȂ����(��发�ł̓��[�㐔�ƌĂсA��������
���[���ɂȂ����(��发�ł̓��[�㐔�ƌĂсA�������� �ƕ\�L)��X�Ƃ��āA
�ƕ\�L)��X�Ƃ��āA �Ƃ��ē����郆�j�^���s��S��(��发�ł́A���[�㐔�ɑΉ����ă��[�Q�ƌĂ�ł��܂�)���Ƃ������Ƃ��킩��܂��B
�Ƃ��ē����郆�j�^���s��S��(��发�ł́A���[�㐔�ɑΉ����ă��[�Q�ƌĂ�ł��܂�)���Ƃ������Ƃ��킩��܂��B
 �̏ꍇ�A
�̏ꍇ�A �Ƃ���ƁA
�Ƃ���ƁA
 �Ƃ���ƁA
�Ƃ���ƁA �C
�C �C
�C �C
�C
����āA
 ���A
���A
��  �@����H
�@����H �ƂȂ�A�p�E���s����܂��B�܂�A �͑Ίp�a��0�ŃG���~�[�g�s��ł���p�E���s��ɂ���č���Ă��܂�(�C�ӂ̃G���~�[�g�s��́A
�͑Ίp�a��0�ŃG���~�[�g�s��ł���p�E���s��ɂ���č���Ă��܂�(�C�ӂ̃G���~�[�g�s��́A �C
�C �C
�C �̐��`�����ō���Ă���)�BX�́Aa�Cc�Cd��3�̎��R�x�������܂��B���X4�̎��R�x���������̂ł����A
�̐��`�����ō���Ă���)�BX�́Aa�Cc�Cd��3�̎��R�x�������܂��B���X4�̎��R�x���������̂ł����A ���1������3�̎��R�x�ɂȂ�܂��B
���1������3�̎��R�x�ɂȂ�܂��B �̏ꍇ�A
�̏ꍇ�A �̎��R�x�������܂��B
�̎��R�x�������܂��B
 �ł́A���R�x��
�ł́A���R�x�� �ƂȂ�A�p�E���s��ɑ�������G���~�[�g�s��8�o�Ă��܂��B���̍s����Q���}���s��ƌ����܂��B8�̃Q���}���s��ɂ���āA
�ƂȂ�A�p�E���s��ɑ�������G���~�[�g�s��8�o�Ă��܂��B���̍s����Q���}���s��ƌ����܂��B8�̃Q���}���s��ɂ���āA �̃��j�^���s����܂��B
�̃��j�^���s����܂��B
1950�N��ɑ��X�ƐV���q���������ꂽ�̂ł����A�o���I����d��Q�ƒ��d��Y�ɂ���Đ�������ƁA�X�s���̒l�ɂ���Ĉȉ��̂悤�ɂȂ�܂��B
�X�s��0�̃��\���́A
�X�s��1�̃��\���́A
�X�s�� �̃o���I���́A
�̃o���I���́A
�X�s�� �̃o���I���́A
�̃o���I���́A
��������A���炩�̋K���������邱�Ƃ��킩���ė��܂����B
�X�g�����W�l�X�A�A�C�\�X�s���̕ۑ��ׂ���c����́A1955�N�A�z�q�A�����q�A�����q����{���q�Ƃ��ăo���I�������闝�_�\���܂����B����3�̗��q�̔g�����Ɋւ���Ώ̐����A�r�c���v�A����C�O�A��ы`�Y��SU(3)�Ώ̐��ŋL�q�ł���Ƃ����A�C�f�A���Ă��܂����B���̑Ώ̐��ɂ��A���\��8�̑g�ݍ��킹�����܂������ł����̂ł����A8�őg�ɂȂ��Ă���o���I���̂����A�z�q�A�����q�A�����q����{���q�Ƃ��Ă��܂��ƁA�c��5�� �Ώ̐��ƍ��v�����A���܂��s���܂���ł����B
�Ώ̐��ƍ��v�����A���܂��s���܂���ł����B
�܂���ɏq�ׂ��z�q�E�����q�ُ̈펥�C���[�����g�ł����A1950�N��㔼�Ƀz�t�X�^�b�^�[�ɂ��A�č��X�^���t�H�[�h��̐��`�������p���āA�t�̐��f�A�t�̏d���f��W�I�Ƃ��āA�d�q��e���Փ˂�����������s���A�z�q�A�����q�����̓����ɐ����̓d�ו��z�̍L����������Ă��邱�Ƃ��킩��A�z�q�E�����q�͊�{�f���q�Ƃ͌����Ȃ����Ƃ��킩���Ă��܂����B
�����ŁA1963�N�A�Q���}���ƃc�o�C�N�́A�����d�ׂ����ASU(3)�Ώ̐��Ɋ�Â��N�H�[�N���f������܂����B�N�H�[�N�́A�X�s�� �̃t�F���~�I���ŁA�d��
�̃t�F���~�I���ŁA�d�� ��up�N�H�[�N(u�ƕ\���܂�)�A�d��
��up�N�H�[�N(u�ƕ\���܂�)�A�d�� ��down�N�H�[�N(d�ƕ\���܂�)�A�d��
��down�N�H�[�N(d�ƕ\���܂�)�A�d�� ��strange�N�H�[�N(s�ƕ\���܂�)����{���q�Ƃ��A���̑g�ݍ��킹�Ńo���I���A���\�����\������A�Ƃ������f���ł��B�N�H�[�N�̎�ނ��t���[�o�[�ƌ����܂��B����ɂ��ƁA�z�q��up�N�H�[�N2��down�N�H�[�N1���琬��A�d��
��strange�N�H�[�N(s�ƕ\���܂�)����{���q�Ƃ��A���̑g�ݍ��킹�Ńo���I���A���\�����\������A�Ƃ������f���ł��B�N�H�[�N�̎�ނ��t���[�o�[�ƌ����܂��B����ɂ��ƁA�z�q��up�N�H�[�N2��down�N�H�[�N1���琬��A�d�� �������A�����q��up�N�H�[�N1��down�N�H�[�N2���琬��A�d�ׂ�
�������A�����q��up�N�H�[�N1��down�N�H�[�N2���琬��A�d�ׂ� �ł��B����G�����\�������Β��Ԏq�Ƃ̑��ݍ�p�́Aup�N�H�[�N�̔����q��
�ł��B����G�����\�������Β��Ԏq�Ƃ̑��ݍ�p�́Aup�N�H�[�N�̔����q�� (�d��
(�d�� )�Cdown�N�H�[�N�̔����q��
)�Cdown�N�H�[�N�̔����q�� (�d��
(�d�� )�Ƃ��āA
)�Ƃ��āA
�z�q(uud)�������q(udd)�{ (
( )�����q(udd)��
)�����q(udd)�� �{�z�q(uud)
�{�z�q(uud) �Ƃ��邱�Ƃɂ������ł��܂����Bu�� ���琬��
���琬�� ���Ԏq�͓d��
���Ԏq�͓d�� �������A
�������A ��d���琬��
��d���琬�� ���Ԏq�͓d��
���Ԏq�͓d�� �������܂��B
�������܂��B ���Ԏq��
���Ԏq�� ���Ԏq�̔����q�ł��B
���Ԏq�̔����q�ł��B
����ɂ��A�z�q�A�����q�̂悤�ȃn�h������A �C
�C �̂悤�ȃ��\��(���Ԏq)�̓N�H�[�N�̕������q�Ƃ���܂����B�܂��A�z�q�ƒ����q�ُ̈펥�C���[�����g(�f���q(����2)���Q��)���A�z�q�A�����q�́Auud�Cudd�Ƃ����\�����玥�C���[�����g���v�Z���邱�Ƃɂ��A�������t�ő傫���̔䂪3�F2�ɂȂ邱�Ƃ������ł��܂��B
�̂悤�ȃ��\��(���Ԏq)�̓N�H�[�N�̕������q�Ƃ���܂����B�܂��A�z�q�ƒ����q�ُ̈펥�C���[�����g(�f���q(����2)���Q��)���A�z�q�A�����q�́Auud�Cudd�Ƃ����\�����玥�C���[�����g���v�Z���邱�Ƃɂ��A�������t�ő傫���̔䂪3�F2�ɂȂ邱�Ƃ������ł��܂��B
3��ނ̃N�H�[�N�� �Ώ̐��������A
�Ώ̐��������A ��3�ʂ�̃N�H�[�N��g�ݍ��킹�āA3�~3�~3�ʂ�̗��q����邱�Ƃ��ł��܂��B27�ʂ��10�ʂ��8�ʂ��8�ʂ��1�ʂ�ɕ��ނł��܂��B
��3�ʂ�̃N�H�[�N��g�ݍ��킹�āA3�~3�~3�ʂ�̗��q����邱�Ƃ��ł��܂��B27�ʂ��10�ʂ��8�ʂ��8�ʂ��1�ʂ�ɕ��ނł��܂��B
���\����8�g�́A
����͐�Ɏ������A�X�s��0�C1�̃��\���̑g�ɑΉ����Ă��܂��B
�o���I����10�g�A8�g(8�g�ł́A10�g��uuu�Cddd�Csss�������܂�)�́A
�������Ɏ������A�X�s�� �C�X�s��
�C�X�s�� �̃o���I���̑g�ɑΉ����Ă��܂��B
�̃o���I���̑g�ɑΉ����Ă��܂��B
���\���̃X�s��0�C1�C�o���I���̃X�s�� �C
�C �ŁA�����N�H�[�N�̑g�ݍ��킹�ŕʂ̃n�h�����ɂȂ��Ă���Ƃ��낪����܂����A�X�s��
�ŁA�����N�H�[�N�̑g�ݍ��킹�ŕʂ̃n�h�����ɂȂ��Ă���Ƃ��낪����܂����A�X�s�� ��'��'�C�X�s��
��'��'�C�X�s�� ��'��'�ƕ\���ƁA�X�s��0 (�����C����)�ƃX�s��
��'��'�ƕ\���ƁA�X�s��0 (�����C����)�ƃX�s�� (�������C������)�ł́A�X�s�������킸�A�X�s��1 (�����C����)�ƁA�X�s��
(�������C������)�ł́A�X�s�������킸�A�X�s��1 (�����C����)�ƁA�X�s�� (�������C������)�ł̓X�s���������Ă��܂��B�����N�H�[�N�̑g�ݍ��킹�ł��A�X�s���������A����Ȃ��A�Ƃ����Ⴂ������܂��B
(�������C������)�ł̓X�s���������Ă��܂��B�����N�H�[�N�̑g�ݍ��킹�ł��A�X�s���������A����Ȃ��A�Ƃ����Ⴂ������܂��B
1964�N�ɃQ���}���̗\���ʂ�� ���q(sss)����������āA�N�H�[�N�E���f���͐M�����l�����܂����B�A���A�N�H�[�N���f���̖��_�Ƃ��āA�Ⴆ��uuu�̑g�ݍ��킹�łł��Ă���
���q(sss)����������āA�N�H�[�N�E���f���͐M�����l�����܂����B�A���A�N�H�[�N���f���̖��_�Ƃ��āA�Ⴆ��uuu�̑g�ݍ��킹�łł��Ă��� ���q�ł́A�X�s��
���q�ł́A�X�s�� �̃t�F���~�I���ł����ĕ����̗��q������̏�Ԃ��Ƃ邱�Ƃ��ł��Ȃ��N�H�[�N���A�����N�H�[�N3��uuu�Ƃ����g�ݍ��킹�ɂȂ�\��������̂��A�Ƃ����^�₪����܂����B���̍��������邽�߂ɁA����1�̎��R�x�����Aup�N�H�[�N�Adown�N�H�[�N�Astrange�N�H�[�N��1��ނł͂Ȃ��A�F���ƌĂ��ʎq��(�X��A��R�A��B�A��G�ƌĂт܂����A�N�H�[�N�ɐF�����Ă���킯�ł͂���܂���)�ŋ�ʂ���A�Ƃ����A�C�f�A���o����܂����B����ɂ��A
�̃t�F���~�I���ł����ĕ����̗��q������̏�Ԃ��Ƃ邱�Ƃ��ł��Ȃ��N�H�[�N���A�����N�H�[�N3��uuu�Ƃ����g�ݍ��킹�ɂȂ�\��������̂��A�Ƃ����^�₪����܂����B���̍��������邽�߂ɁA����1�̎��R�x�����Aup�N�H�[�N�Adown�N�H�[�N�Astrange�N�H�[�N��1��ނł͂Ȃ��A�F���ƌĂ��ʎq��(�X��A��R�A��B�A��G�ƌĂт܂����A�N�H�[�N�ɐF�����Ă���킯�ł͂���܂���)�ŋ�ʂ���A�Ƃ����A�C�f�A���o����܂����B����ɂ��A ���q��
���q��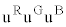 �̂悤�ɍ\������Ă��ăp�E���̔r�����������Ă���A�Ɛ�������܂����B�o���I���ł́A�N�H�[�N�́A3�̐F�ׂ̏d�ˍ��킹�����F�ɂȂ�悤�ɑg�ݍ��킳��܂��B�����Ɋϑ������N�H�[�N��
�̂悤�ɍ\������Ă��ăp�E���̔r�����������Ă���A�Ɛ�������܂����B�o���I���ł́A�N�H�[�N�́A3�̐F�ׂ̏d�ˍ��킹�����F�ɂȂ�悤�ɑg�ݍ��킳��܂��B�����Ɋϑ������N�H�[�N�� ��1�d���ɂȂ��Ă��āA
��1�d���ɂȂ��Ă��āA
�̂悤�ɋL�q���� �Q�[�W�ϊ��ɑ��ĕs�ςł��B�n�h����������Ƃ��A�N�H�[�N�Ɣ��N�H�[�N�Ƃ̑g�ݍ��킹�ɂȂ�悤�Ƀ��\�����ł��܂��B���N�H�[�N�̐F�ׂ̓N�H�[�N�̕�F�ɂȂ�܂��B���Ԃ͐��F�A���͉��F�A���͎��Ƃ��������ł��B���\���́A�N�H�[�N�̐F�ׂ̏d�ˍ��킹�����F�ɂȂ�悤�ɁA�ԂƔ��ԂŔ��A�Ɣ��Ŕ��A�Ɣ��Ŕ��ƂȂ�悤�ȑg�ݍ��킹������������܂��B�Ⴆ�A����G�������݂�\�������Β��Ԏq�́A
�Q�[�W�ϊ��ɑ��ĕs�ςł��B�n�h����������Ƃ��A�N�H�[�N�Ɣ��N�H�[�N�Ƃ̑g�ݍ��킹�ɂȂ�悤�Ƀ��\�����ł��܂��B���N�H�[�N�̐F�ׂ̓N�H�[�N�̕�F�ɂȂ�܂��B���Ԃ͐��F�A���͉��F�A���͎��Ƃ��������ł��B���\���́A�N�H�[�N�̐F�ׂ̏d�ˍ��킹�����F�ɂȂ�悤�ɁA�ԂƔ��ԂŔ��A�Ɣ��Ŕ��A�Ɣ��Ŕ��ƂȂ�悤�ȑg�ݍ��킹������������܂��B�Ⴆ�A����G�������݂�\�������Β��Ԏq�́A
�Ƃ����N�H�[�N�̑g�ݍ��킹�ɂȂ�܂����A �ł́Au���ԂȂ�
�ł́Au���ԂȂ� �����ԁAu���Ȃ�
�����ԁAu���Ȃ� �����Au���Ȃ�
�����Au���Ȃ� �����Ƃ����\���ɂȂ�܂��B
�����Ƃ����\���ɂȂ�܂��B
�N�H�[�N�̔g�����X�s�m���� (
(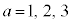 )�Ƃ��āA
)�Ƃ��āA �̃Q�[�W�ϊ�
�̃Q�[�W�ϊ� (a��a��ł͂Ȃ��Y���ł�)���{����
(a��a��ł͂Ȃ��Y���ł�)���{���� ���f�B���b�N�������́A�Q�[�W�ϊ��ŕs�ςȉ��ɂȂ�܂��B
���f�B���b�N�������́A�Q�[�W�ϊ��ŕs�ςȉ��ɂȂ�܂��B �ɑ����郆�j�^���s��̎��R�x��8�ŁA8�̃Q���}���s��
�ɑ����郆�j�^���s��̎��R�x��8�ŁA8�̃Q���}���s�� �ɑ���
�ɑ��� (
( )�Ƃ��āA�Q�[�W��
)�Ƃ��āA�Q�[�W�� ���O���[�I����\���܂��B�����ŁA����
���O���[�I����\���܂��B�����ŁA���� �͋��ϔ���
�͋��ϔ��� �ɒu�������܂��B
�ɒu�������܂��B ��
��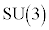 �Q�[�W���ݍ�p�̋�����\�������萔�ł��B�O���[�I���̓N�H�[�N���m��\�荇�킹��͂ŁA�N�H�[�N�Ԃ��O���[�I�����}��邱�Ƃɂ�苭���͂������܂��B���̗͂ɂ��A�N�H�[�N�͒P�̂ł͑��݂��邱�Ƃ��ł����A2�܂���3�̑g�ɂȂ��đ��݂��܂��B������N�H�[�N�������ƌ����܂��B���̂��ߌ����_�܂łɁA�P�̃N�H�[�N�������I�Ɋm�F���邱�Ƃ͂ł��Ă��܂���B
�Q�[�W���ݍ�p�̋�����\�������萔�ł��B�O���[�I���̓N�H�[�N���m��\�荇�킹��͂ŁA�N�H�[�N�Ԃ��O���[�I�����}��邱�Ƃɂ�苭���͂������܂��B���̗͂ɂ��A�N�H�[�N�͒P�̂ł͑��݂��邱�Ƃ��ł����A2�܂���3�̑g�ɂȂ��đ��݂��܂��B������N�H�[�N�������ƌ����܂��B���̂��ߌ����_�܂łɁA�P�̃N�H�[�N�������I�Ɋm�F���邱�Ƃ͂ł��Ă��܂���B
�f���q(����4)�ɂÂ��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@����C
�@����C �ɑ��āA2�s2��̃��j�^���s��U�ŕ\�����Q�[�W�ϊ�����p������
�ɑ��āA2�s2��̃��j�^���s��U�ŕ\�����Q�[�W�ϊ�����p������


 �Ƃ��āA
�Ƃ��āA
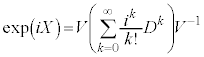





 �Ƃ���ƁA
�Ƃ���ƁA

 �@����H
�@����H





 ���f�B���b�N�������́A�Q�[�W�ϊ��ŕs�ςȉ��ɂȂ�܂��B
���f�B���b�N�������́A�Q�[�W�ϊ��ŕs�ςȉ��ɂȂ�܂��B ���O���[�I����\���܂��B�����ŁA����
���O���[�I����\���܂��B�����ŁA����