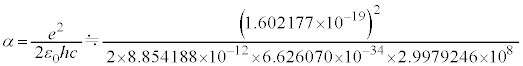�f���q����̂Â��ł��B
�V�����[�f�B���K�[�������ŕ����̗��q�������ꍇ�́A���q�Ԃ̑��ݍ�p��g�ݍ����������������ƂɂȂ�܂��B���G�ʼn�͓I�ɉ����͍̂���Ȃ̂ŁA�ߎ����s������A�d�q�v�Z�@��p���Đ��l�I�ɉ������ƂɂȂ�܂��B2���q�����헱�q�̏ꍇ�A�ʒu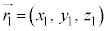 �ɂ���X�s��
�ɂ���X�s��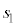 �̗��q1�ƁA�ʒu
�̗��q1�ƁA�ʒu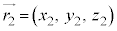 �ɂ���X�s��
�ɂ���X�s��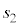 �̗��q2�̈ʒu�G�l���M�[��
�̗��q2�̈ʒu�G�l���M�[��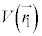 �C
�C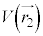 �C���q1�Ɨ��q2�̑��ݍ�p�ɂ��G�l���M�[��
�C���q1�Ɨ��q2�̑��ݍ�p�ɂ��G�l���M�[��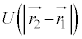 �Ƃ��āA�V�����[�f�B���K�[�������́A
�Ƃ��āA�V�����[�f�B���K�[�������́A
�ł��B���̉���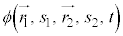 �Ƃ��āA���q1�Ɨ��q2�����ւ������̉���
�Ƃ��āA���q1�Ɨ��q2�����ւ������̉���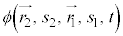 �ƂȂ�܂����Ak��萔�Ƃ��āA
�ƂȂ�܂����Ak��萔�Ƃ��āA
�Ə������Ƃ��܂��B������x���q1�Ɨ��q2�����ւ���ƁA�ŏ��̏�Ԃɖ߂�̂ŁA
�ƂȂ�܂��B�܂�A �C
�C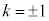 �ł��B
�ł��B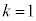 �̏ꍇ�A
�̏ꍇ�A
�ƂȂ藱�q�����ւ��Ă����̒l�͓����ł��B���̂Ƃ��A���헱�q�̌����ɂ��đΏ̂ł���A�Ƃ��������������܂��B���q�Ȃǂ̃X�s���������l���Ƃ闱�q�ł́A���q�̌����ɂ��đΏ̂ŁA�����������q���{�\��(�{�[�Y���q)�ƌ����܂��B�{�\���́A�����̗��q��������Ԃ���邱�Ƃ��\�ŁA�{�[�Y�E�A�C���V���^�C�����v�ɏ]���܂��B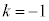 �̏ꍇ�A
�̏ꍇ�A
�ƂȂ�A���q�̓���ւ��ɂ�蕄�����ω����܂����A���̂Ƃ��A���헱�q�̌����ɂ��Ĕ��Ώ̂ł���A�Ƃ��������������܂��B�d�q�A�z�q�A�����q�̃X�s����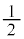 �ł����A�X�s����
�ł����A�X�s���� �C
�C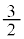 �C����Ƃ����悤�Ȓl���Ƃ闱�q�ł́A���q�̌����ɂ��Ĕ��Ώ̂ŁA�����������q���t�F���~�I��(�t�F���~���q)�ƌ����܂��B�t�F���~�I���ł́A���q�̌����ɂ��ďd�ˍ��킹��ƁA
�C����Ƃ����悤�Ȓl���Ƃ闱�q�ł́A���q�̌����ɂ��Ĕ��Ώ̂ŁA�����������q���t�F���~�I��(�t�F���~���q)�ƌ����܂��B�t�F���~�I���ł́A���q�̌����ɂ��ďd�ˍ��킹��ƁA
�ƂȂ��Ă��܂��A���݊m����0�ɂȂ��Ă��܂��܂��B�]���āA�X�s�����������̃t�F���~�I���ł�1�̏�Ԃ��̓��헱�q����߂邱�Ƃ͂ł��܂���B������p�E���̔r�������ƌ����܂��B�t�F���~�I���́A�t�F���~�E�f�B���b�N���v�ɏ]���܂��B
���q�̉�͂��s���V�����[�f�B���K�[�������́A�f���q�̂悤�ɍ����Ŕ�щ�鑊�Θ_�I�ȏ��������Ƃ��ł��܂���B�V�����[�f�B���K�[�������̌��ɂȂ����A����m�̗��q�̃G�l���M�[E�Ɖ^����p�̊Ԃ̊W���F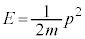 �ɑ���A�A�C���V���^�C�������������Θ_�̎��F
�ɑ���A�A�C���V���^�C�������������Θ_�̎��F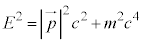 �C����c��
�C����c��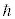 ��1�Ƃ���P�ʌn��
��1�Ƃ���P�ʌn�� �ɂ����āA�V�����[�f�B���K�[�����������Ƃ��ɍs�����ϊ��F
�ɂ����āA�V�����[�f�B���K�[�����������Ƃ��ɍs�����ϊ��F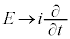 �C
�C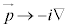 (
(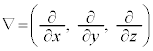 )���{���ƁA���Θ_���l�������������Ƃ��āA
)���{���ƁA���Θ_���l�������������Ƃ��āA
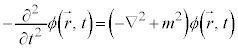 �@����@
�@����@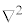 ��2�K�̔����ɂȂ�Ȃ玞��t �ɂ��Ă�2�K�̔����ɂȂ�)�̂��߂ɁA���Ԃɂ���2�K�̔����������ŁA�m�����x�����ɂȂ肤��Ƃ������������Ă��܂���(�V�����[�f�B���K�[�́A�V�����[�f�B���K�[���������o�ȑO�ɇ@�ɓ��B���Ă����̂ł����A�m�����߂��ł����A�N�[�����͂̈ʒu�G�l���M�[�����ĉ����Ă��{�[�A���a�������Ȃ����ߎ̂ĂĂ��܂��������ł�)�B�܂����̃G�l���M�[���������\(�@�̉E�ӂ�
��2�K�̔����ɂȂ�Ȃ玞��t �ɂ��Ă�2�K�̔����ɂȂ�)�̂��߂ɁA���Ԃɂ���2�K�̔����������ŁA�m�����x�����ɂȂ肤��Ƃ������������Ă��܂���(�V�����[�f�B���K�[�́A�V�����[�f�B���K�[���������o�ȑO�ɇ@�ɓ��B���Ă����̂ł����A�m�����߂��ł����A�N�[�����͂̈ʒu�G�l���M�[�����ĉ����Ă��{�[�A���a�������Ȃ����ߎ̂ĂĂ��܂��������ł�)�B�܂����̃G�l���M�[���������\(�@�̉E�ӂ�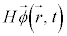 �Ə�����H���n�~���g�j�A���ƌ����܂����A
�Ə�����H���n�~���g�j�A���ƌ����܂����A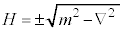 �̂悤�Ȍ`�ɏ����Ă��܂�)�ŁA�G�l���M�[���̉����\�Ȃ�A�G�l���M�[���̏�Ԃ���A���G�l���M�[�̒Ⴂ���̏�Ԃɂǂ�ǂ�J�ڂ��Ă��܂��ł͂Ȃ����A�Ƃ�������N���Ȃ���܂����B�Ⴆ�·@��
�̂悤�Ȍ`�ɏ����Ă��܂�)�ŁA�G�l���M�[���̉����\�Ȃ�A�G�l���M�[���̏�Ԃ���A���G�l���M�[�̒Ⴂ���̏�Ԃɂǂ�ǂ�J�ڂ��Ă��܂��ł͂Ȃ����A�Ƃ�������N���Ȃ���܂����B�Ⴆ�·@��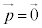 (���q���Î~���Ă���)�C�܂�A
(���q���Î~���Ă���)�C�܂�A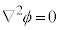 �Ƃ���ƁA
�Ƃ���ƁA
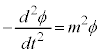 �@����A
�@����A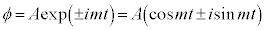 �Ƃ������������܂��B�G�l���M�[�̌ŗL�l�́A�G�l���M�[���Z�q
�Ƃ������������܂��B�G�l���M�[�̌ŗL�l�́A�G�l���M�[���Z�q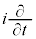 ��ϕ�ɂ����āA
��ϕ�ɂ����āA
���ŗL�l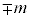 �������܂��B����c��1�Ƃ���P�ʌn�ōl���Ă����̂ŁA����́A����m�̗��q�̐Î~�G�l���M�[
�������܂��B����c��1�Ƃ���P�ʌn�ōl���Ă����̂ŁA����́A����m�̗��q�̐Î~�G�l���M�[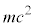 �ɐ����̕������������̂ɂȂ�܂��B�܂�@�ł͕��̃G�l���M�[�����蓾��̂ł��B�܂��A�@�ł́A�m�����x��
�ɐ����̕������������̂ɂȂ�܂��B�܂�@�ł͕��̃G�l���M�[�����蓾��̂ł��B�܂��A�@�ł́A�m�����x��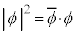 �ł͂Ȃ��A
�ł͂Ȃ��A
�ŗ^�����A�m�����x�����ɂȂ蓾�Ă��܂��܂��B
����ɑ��āA�C�M���X�̃f�B���b�N�́A��ԂƎ��Ԃ��Ɉ����������̎��Ԕ�����1�K�ɂ��邽�߂ɁA�����Ă݂�A
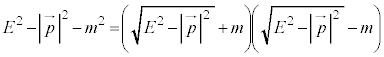 �@����B
�@����B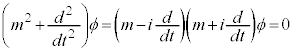 �Ƃ��ĉ����悤�Ȃ��̂ł��B���Θ_�ł́A�h�E�u���C�̊W�����
�Ƃ��ĉ����悤�Ȃ��̂ł��B���Θ_�ł́A�h�E�u���C�̊W�����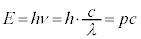 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA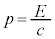 ��4���^���ʃx�N�g���̑�0�����ƍl���A�^���ʂ�
��4���^���ʃx�N�g���̑�0�����ƍl���A�^���ʂ�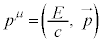 �C
�C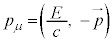 �ƍl���܂��B4���^���ʃx�N�g���̑傫���́A
�ƍl���܂��B4���^���ʃx�N�g���̑傫���́A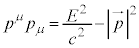 �ƂȂ�܂�)�Ɋ�Â��āA1928�N�A���Ԃɂ��Ă���Ԃɂ��Ă�1�K�̔����ŋL�q�����f�B���b�N��������҂ݏo���܂����B���o�̉ߒ����ʉ��͐�发�Ɉς˂܂����A�f�B���b�N�������́A
�ƂȂ�܂�)�Ɋ�Â��āA1928�N�A���Ԃɂ��Ă���Ԃɂ��Ă�1�K�̔����ŋL�q�����f�B���b�N��������҂ݏo���܂����B���o�̉ߒ����ʉ��͐�发�Ɉς˂܂����A�f�B���b�N�������́A
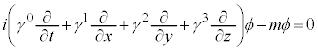 �@����C
�@����C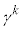 (k�́Ak��Ƃ����Ӗ��̎w���ł͂Ȃ��A�Y���ł��B
(k�́Ak��Ƃ����Ӗ��̎w���ł͂Ȃ��A�Y���ł��B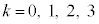 )�́A�K���}�s���ƌĂ��4�s4��̍s��ŁA��ɏo�Ă���2�s2��̃p�E���s��
)�́A�K���}�s���ƌĂ��4�s4��̍s��ŁA��ɏo�Ă���2�s2��̃p�E���s��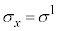 �C
�C �C
�C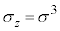 (�f���q�̇H��)�ƒP�ʍs��I��p���āA
(�f���q�̇H��)�ƒP�ʍs��I��p���āA
�Ƃ���ƇB�̂悤�ɕό`�ł���̂ł�(���̂悤�ȍs��͑��ɂ�����܂��B��L�̃K���}�s����f�B���b�N�\���ƌ����܂�)�B�����ł́A�g����ϕ�́A4�����̃X�s�m��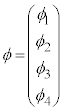 �ƂȂ�܂��B�C�͑��Θ_�I�ȋL�q������ƁA
�ƂȂ�܂��B�C�͑��Θ_�I�ȋL�q������ƁA
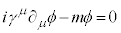 �@����D
�@����D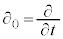 (�����ł�
(�����ł�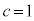 �Ƃ��Ă��܂����A�{����
�Ƃ��Ă��܂����A�{����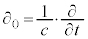 �ł�)�C
�ł�)�C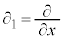 �C
�C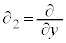 �C
�C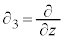 �ł�(���Ȃ݂�
�ł�(���Ȃ݂�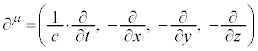 �ł�)�B�܂��A
�ł�)�B�܂��A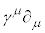 �́A
�́A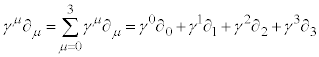 (�㑤�̓Y���Ɖ����̓Y������v�����Ęa���Ƃ邱�Ƃ��k���ƌ����܂�)�̂��Ƃł��B��发�ɂ���ẮA�K���}�s��Ƃ̏k���
(�㑤�̓Y���Ɖ����̓Y������v�����Ęa���Ƃ邱�Ƃ��k���ƌ����܂�)�̂��Ƃł��B��发�ɂ���ẮA�K���}�s��Ƃ̏k���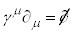 �Ə����Ă�����̂�����܂��B���̏������Ńf�B���b�N�������D�́A
�Ə����Ă�����̂�����܂��B���̏������Ńf�B���b�N�������D�́A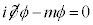 �ƊȒP�ɂȂ�܂��B�f�B���b�N���������A���q���Î~���Ă���Ƃ��čl���Ă݂܂��B�܂�A�^���ʂ��[���A�C��
�ƊȒP�ɂȂ�܂��B�f�B���b�N���������A���q���Î~���Ă���Ƃ��čl���Ă݂܂��B�܂�A�^���ʂ��[���A�C��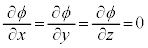 �Ƃ���ƁA
�Ƃ���ƁA
�����̉��́A
�ƂȂ�܂��B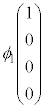 ��
��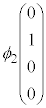 �̓G�l���M�[���A
�̓G�l���M�[���A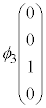 ��
��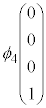 �̓G�l���M�[���ɂȂ�A�f�B���b�N�������ł��G�l���M�[���̉����o�Ă��܂��B
�̓G�l���M�[���ɂȂ�A�f�B���b�N�������ł��G�l���M�[���̉����o�Ă��܂��B
�d�q�́A�p�E���̔r�������ɏ]���A����̏�Ԃ��̓d�q����L���邱�Ƃ͋֎~����Ă���̂ŁA�f�B���b�N�́A�^��Ƃ̓G�l���M�[���̏�Ԃ��S�Ė��ߐs������Ă�����(�f�B���b�N�̊C�ƌĂ�Ă��܂�)�ŁA���̒��ɐ�������E���G�l���M�[���̉��Ȃ̂�(���̃G�l���M�[�̓d�q�������Ă���̂Ő��̃G�l���M�[�������܂�)�ƍl���܂����B��ɁA���̋�E�͓d�q�������q�Ő��d�ׂ������z�d�q�ł���Ƃ���A1932�N�ɂ́A�č��̃A���_�[�\�����F�����̒��ɓd�q�Ɠ������ʂŋt�̓d�ׂ������q(�z�d�q)�����A�f�B���b�N�̍l����(��E���_�ƌ����܂�)���F�߂��܂����B�܂��A�f�B���b�N�������������ē�����4�̉��́A�G�l���M�[���̓d�q�̏�����X�s���A�������X�s���A�G�l���M�[���̓d�q�̏�����X�s���A�������X�s����\��(��E�����z�q�Ȃ̂ŁA���z�q�̃G�l���M�[�͐��ŃX�s�����t�ɂȂ�܂��B���z�q���������������͇D�ł͂Ȃ��A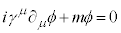 �ł�)�ƍl�����Ă��܂��B�^��̒��ɂł����G�l���M�[���̋�E(�z�d�q)�ɓd�q���������ނƂ���ň���ɂȂ�A����ꂽ�d�q�̃G�l���M�[�����qγ�Ƃ��Ĕ�яo���Ă��܂��B�����d�q�E�z�d�q�Ώ����ƌ����A
�ł�)�ƍl�����Ă��܂��B�^��̒��ɂł����G�l���M�[���̋�E(�z�d�q)�ɓd�q���������ނƂ���ň���ɂȂ�A����ꂽ�d�q�̃G�l���M�[�����qγ�Ƃ��Ĕ�яo���Ă��܂��B�����d�q�E�z�d�q�Ώ����ƌ����A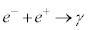 �ƕ\���܂��B�����̂œd�q�Ɛ��E����������̂Ɏ��Ă��܂��B�t�Ɍ��qγ�̃G�l���M�[�ɂ���Đ^�̕��G�l���M�[�̓d�q���G�l���M�[���̏�ԂɑJ�ڂ��āA�^�ɋ�E���ł��ėz�d�q���������錻�ۂ��ΐ����ƌ����A
�ƕ\���܂��B�����̂œd�q�Ɛ��E����������̂Ɏ��Ă��܂��B�t�Ɍ��qγ�̃G�l���M�[�ɂ���Đ^�̕��G�l���M�[�̓d�q���G�l���M�[���̏�ԂɑJ�ڂ��āA�^�ɋ�E���ł��ėz�d�q���������錻�ۂ��ΐ����ƌ����A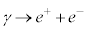 �ƕ\���܂��B
�ƕ\���܂��B
���ɏq�ׂ܂������A�i�g���E����2s�O��(�����łȂ��A���J�������̍ŊO�ks�O��)�ɂ͓d�q1�݂̂�����A���̓d�q�̊p�^���ʂ͑ł����������̂ŁA�O���p�^���ʂ�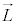 �C�X�s���p�^���ʂ�
�C�X�s���p�^���ʂ�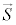 �Ƃ��āA�S�p�^����
�Ƃ��āA�S�p�^����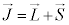 �́A�X�s��
�́A�X�s��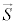 �̉e���݂̂ɂȂ�܂��B�X�y�N�g���̔��\�����ϑ�����ƁA������������ɃX�s���̉e�����Ȃ��Ƃ��́A���C�ʎq��M�̈Ⴂ�ɂ��e���ʊԂ̃G�l���M�[����
�̉e���݂̂ɂȂ�܂��B�X�y�N�g���̔��\�����ϑ�����ƁA������������ɃX�s���̉e�����Ȃ��Ƃ��́A���C�ʎq��M�̈Ⴂ�ɂ��e���ʊԂ̃G�l���M�[����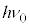 (
( �́A�O���p�^���ʂ̕����̂܂��Ɏ�U��^������ۂ̎��g���Ń��[���A���g���ƌĂ�܂�)�ƂȂ�A����������ăX�s���̉e���ׂ�ƁA
�́A�O���p�^���ʂ̕����̂܂��Ɏ�U��^������ۂ̎��g���Ń��[���A���g���ƌĂ�܂�)�ƂȂ�A����������ăX�s���̉e���ׂ�ƁA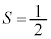 �Ȃ̂ŁA�X�s��
�Ȃ̂ŁA�X�s��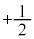 �C
�C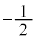 �̃G�l���M�[���́A����������Ȃ��Ƃ��Ɣ�r���āA
�̃G�l���M�[���́A����������Ȃ��Ƃ��Ɣ�r���āA �C
�C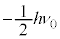 �ɂȂ肻���Ȃ̂ł����A���ۂ̊ϑ��l�́A
�ɂȂ肻���Ȃ̂ł����A���ۂ̊ϑ��l�́A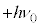 �C
�C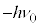 �ƂȂ�܂��B1921�N�Ƀh�C�c(��ɕč��ɈڏZ)�̃����f�́A���ۂ̊ϑ��l�𗝘_�l��
�ƂȂ�܂��B1921�N�Ƀh�C�c(��ɕč��ɈڏZ)�̃����f�́A���ۂ̊ϑ��l�𗝘_�l��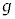 �{���Ƃ��āA�X�s���ɂ�鎥�C���[�����g�́A�O���p�^���ʂɂ�鎥�C���[�����g��
�{���Ƃ��āA�X�s���ɂ�鎥�C���[�����g�́A�O���p�^���ʂɂ�鎥�C���[�����g��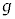 �{�ɂȂ��Ă��āA�ق�
�{�ɂȂ��Ă��āA�ق�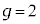 ���ƌ��_���܂����B����
���ƌ��_���܂����B����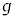 �������f��g���q�ƌ����܂��B�d����̉e�����l������V�����[�f�B���K�[�������������ۂɁA�S�p�^���ʂ�
�������f��g���q�ƌ����܂��B�d����̉e�����l������V�����[�f�B���K�[�������������ۂɁA�S�p�^���ʂ�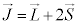 �Ƃ��ĉ����A2�{�̎��C���[�����g�̌��ʂ������܂��B
�Ƃ��ĉ����A2�{�̎��C���[�����g�̌��ʂ������܂��B
�d����(�d��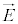 �C�������x
�C�������x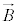 )���x
)���x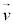 �ʼn^������d��q�́A���[�����c��
�ʼn^������d��q�́A���[�����c��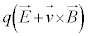 ���܂��B������l�������S�G�l���M�[H (�n�~���g�j�A���A�d���ꂪ�Ȃ��Ƃ��́A�^���G�l���M�[�݂̂�
���܂��B������l�������S�G�l���M�[H (�n�~���g�j�A���A�d���ꂪ�Ȃ��Ƃ��́A�^���G�l���M�[�݂̂�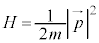 )�́A�x�N�g���E�|�e���V������
)�́A�x�N�g���E�|�e���V������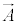 �C�X�J���[�E�|�e���V������φ�Ƃ���(
�C�X�J���[�E�|�e���V������φ�Ƃ���( �C
�C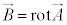 )�A
)�A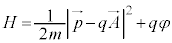 �ƕ\���܂��B
�ƕ\���܂��B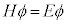 �ɂ����āA
�ɂ����āA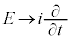 �C
�C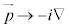 �Ƃ���A�V�����[�f�B���K�[�������������܂��B�����ŁA
�Ƃ���A�V�����[�f�B���K�[�������������܂��B�����ŁA
�����ŁA�������x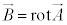 ����l�Ƃ���z����
����l�Ƃ���z����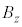 (���)�̂ݎ��Ƃ���ƁA
(���)�̂ݎ��Ƃ���ƁA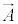 �́A
�́A
�Ƃ����܂��B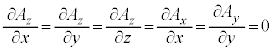 �C
�C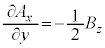 �C
�C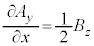 �Ȃǂɂ��A���ۂɁA
�Ȃǂɂ��A���ۂɁA
�ł��B����ɁA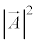 �����A
�����A
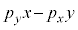 �͋O���p�^����
�͋O���p�^����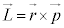 ��z����
��z����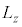 �ł��B�O�q�̂悤�ɁA���Z�q
�ł��B�O�q�̂悤�ɁA���Z�q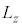 ��
��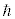 �̐����{�Ƃ����ŗL�l�����̂ŁA��Ԋ�{�I��
�̐����{�Ƃ����ŗL�l�����̂ŁA��Ԋ�{�I��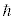 ���l����ƁA�E�ӑ�2���́A
���l����ƁA�E�ӑ�2���́A
�ƂȂ�܂��B�d�q�̏ꍇ��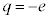 �C�܂��A
�C�܂��A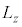 ���X�s���p�^����
���X�s���p�^����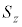 �Ƃ���ƁA
�Ƃ���ƁA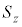 �̌ŗL�l��
�̌ŗL�l��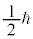 �Ȃ̂ŁA�����f��g���q��t���āA
�Ȃ̂ŁA�����f��g���q��t���āA
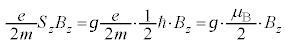 �@(
�@(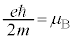 �̓{�[�A���q�ł�)
�̓{�[�A���q�ł�)
�d���ꒆ�̃f�B���b�N�������D�F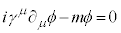 �ł́A��L�̃n�~���g�j�A���Ɠ��l�ɁA4���x�N�g���E�|�e���V������
�ł́A��L�̃n�~���g�j�A���Ɠ��l�ɁA4���x�N�g���E�|�e���V������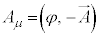 �Ƃ��āA
�Ƃ��āA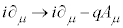 �Ƃ����u���������s���܂��B
�Ƃ����u���������s���܂��B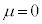 ��
��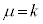 (
(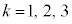 )���Aφ�C
)���Aφ�C ��p���ď����ƁA�D�́A
��p���ď����ƁA�D�́A
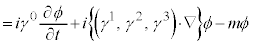 �@(��)
�@(��)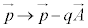 ��
��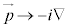 �Ƃ����
�Ƃ���� �C�܂�A
�C�܂�A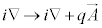 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA
�Ƃ���ƁA���́A
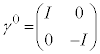 �������āA
�������āA
�𗘗p����ƁA���́A
�����ŁA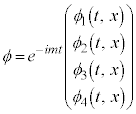 �C
�C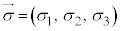 �Ƃ����A�X�s�m�[���̏�2�����ƁA��2�������ď����ƁA
�Ƃ����A�X�s�m�[���̏�2�����ƁA��2�������ď����ƁA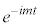 �Ŋ����āA
�Ŋ����āA
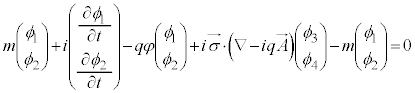 �@����E
�@����E
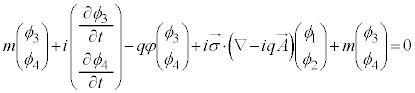 �@����F
�@����F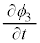 �C
�C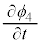 �C
�C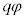 �����A
�����A
������E�ɑ������ƁA
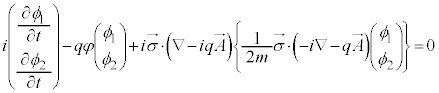 ��
�� 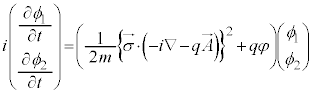 �@����G
�@����G
�����ŁA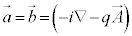 �ƌ����(�������Z�q
�ƌ����(�������Z�q �������Ă���̂�
�������Ă���̂�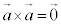 �ƂȂ�Ȃ��̂Œ��ӂ��Ă�������)�A
�ƂȂ�Ȃ��̂Œ��ӂ��Ă�������)�A
�ƂȂ�̂ŁA
������G�́A
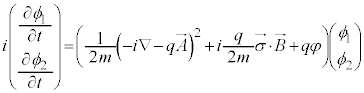 �@����H
�@����H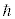 ���I�ɓ���ď����ƁA
���I�ɓ���ď����ƁA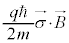 �ƂȂ�A����͐�ɍl�@�����d���ꒆ�̃X�s���̃G�l���M�[�ł��B�H���E�ӂ́A�X�s��
�ƂȂ�A����͐�ɍl�@�����d���ꒆ�̃X�s���̃G�l���M�[�ł��B�H���E�ӂ́A�X�s��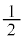 �̌��ʂ��������V�����[�f�B���K�[�������̃n�~���g�j�A���Ɉ�v���܂�(�Ƃ������Ƃ́A�f�B���b�N�������́A�X�s��
�̌��ʂ��������V�����[�f�B���K�[�������̃n�~���g�j�A���Ɉ�v���܂�(�Ƃ������Ƃ́A�f�B���b�N�������́A�X�s��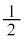 �̃t�F���~�I���ɑΉ�����������Ƃ������Ƃł�)�B�܂��A�����f��g���q��
�̃t�F���~�I���ɑΉ�����������Ƃ������Ƃł�)�B�܂��A�����f��g���q��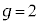 �ł��邱�Ƃ��K�R�I�Ɍ����܂�(�܂�A�O���p�^���ʂƃX�s���p�^���ʂ������l�ł���Ƃ��A�X�s���ɂ�鎥�C���[�����g���O���p�^���ʂɂ�鎥�C���[�����g��2�{�ɂȂ�A�Ƃ����̂͑��Θ_�I���ʁA�Ƃ������Ƃł�)�B�Ƃ��낪�A�������ʂł́A�����l��
�ł��邱�Ƃ��K�R�I�Ɍ����܂�(�܂�A�O���p�^���ʂƃX�s���p�^���ʂ������l�ł���Ƃ��A�X�s���ɂ�鎥�C���[�����g���O���p�^���ʂɂ�鎥�C���[�����g��2�{�ɂȂ�A�Ƃ����̂͑��Θ_�I���ʁA�Ƃ������Ƃł�)�B�Ƃ��낪�A�������ʂł́A�����l��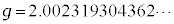 �Ɛ��m�ɋ��߂��Ă���(�����̑���ł͍ł����x�̍��������l�������ł�)�A������2���炸��܂��B
�Ɛ��m�ɋ��߂��Ă���(�����̑���ł͍ł����x�̍��������l�������ł�)�A������2���炸��܂��B
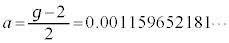 �@����I
�@����I
�N���C���E�S���h���̕������@��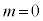 �Ƃ���Ɠd���g�̔g���������A
�Ƃ���Ɠd���g�̔g���������A
�ɂȂ�܂��B�܂�A�d���g��`������q�͎���0�̗��q�ł��邱�Ƃ��Ӗ����܂��B�f�B���b�N��������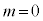 �Ƃ������̂����C���������ƌ����܂��B���̂Ƃ��́A�g����
�Ƃ������̂����C���������ƌ����܂��B���̂Ƃ��́A�g���� ��2�����X�s�m���ɂȂ�܂��B
��2�����X�s�m���ɂȂ�܂��B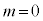 �ł͓d�q���������Ƃ��ł����A���炭�Y����Ă��܂������A���̕������ł��p���e�B�[(��ԑΏ̐��A��Ԕ��]�ŕs�ς̂Ƃ�1�C���]����Ƃ�
�ł͓d�q���������Ƃ��ł����A���炭�Y����Ă��܂������A���̕������ł��p���e�B�[(��ԑΏ̐��A��Ԕ��]�ŕs�ς̂Ƃ�1�C���]����Ƃ�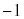 )���ۑ����ꂸ�A��q���܂����A1957�N�Ɏア���ݍ�p�ɂ�����p���e�B�[��ۑ��������I�Ɋm�F����Č�������܂����B����ȍ~�A�ア���ݍ�p�ɂ����W���Ȃ��Ƃ���������L����j���[�g���m���L�q����������ƍl�����Ă����̂ł����A�ŋ߁A�j���[�g���m�ɂ͏������Ȃ�������ʂ����邱�Ƃ��킩���Ă��āA���_�̌��������K�v�ɂȂ��Ă��܂��B
)���ۑ����ꂸ�A��q���܂����A1957�N�Ɏア���ݍ�p�ɂ�����p���e�B�[��ۑ��������I�Ɋm�F����Č�������܂����B����ȍ~�A�ア���ݍ�p�ɂ����W���Ȃ��Ƃ���������L����j���[�g���m���L�q����������ƍl�����Ă����̂ł����A�ŋ߁A�j���[�g���m�ɂ͏������Ȃ�������ʂ����邱�Ƃ��킩���Ă��āA���_�̌��������K�v�ɂȂ��Ă��܂��B
�f�B���b�N�̋�E���_�ŁA�d�q�E�z�d�q�ΐ����̂��߂ɂ́A�^��`���d���g�̌��q��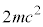 (m�F�d�q�̎���)�ȏ�̃G�l���M�[�������Ă���K�v������܂��B�d�q�Ɨz�d�q���e�X
(m�F�d�q�̎���)�ȏ�̃G�l���M�[�������Ă���K�v������܂��B�d�q�Ɨz�d�q���e�X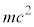 �Ƃ����Î~�G�l���M�[��������ł��B���q�̃G�l���M�[���s������ƁA���ɓd�q���������Ă������ɕ��̃G�l���M�[�̋�E�ɖ߂��Ă��܂��܂��B���Ɍ��q(�łȂ��Ă��N�H�[�N�����������Ă���O���[�I���̂悤�ȗ��q�ł��悢�̂ł���)��
�Ƃ����Î~�G�l���M�[��������ł��B���q�̃G�l���M�[���s������ƁA���ɓd�q���������Ă������ɕ��̃G�l���M�[�̋�E�ɖ߂��Ă��܂��܂��B���Ɍ��q(�łȂ��Ă��N�H�[�N�����������Ă���O���[�I���̂悤�ȗ��q�ł��悢�̂ł���)��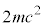 ��ꡂ��ɒ�����G�l���M�[�������Đ^�ɓ����Ă���ƁA�������̓d�q�E�z�d�q�����A�����Ă݂�A�^�U�d�̂̂悤�ȓ��������܂��B������^����ƌ����܂��B�d�q���^�ɑ��݂���Ƃ��A�d�q�̎��͂��U�d�̂̂悤�ɓ����A�d�q�̉��ɓd�C�o�Ɏq�������ēd������A�d�q�ɂ��^�̓d����Օ����܂�(�^��Օ��ƌ����܂�)�B
��ꡂ��ɒ�����G�l���M�[�������Đ^�ɓ����Ă���ƁA�������̓d�q�E�z�d�q�����A�����Ă݂�A�^�U�d�̂̂悤�ȓ��������܂��B������^����ƌ����܂��B�d�q���^�ɑ��݂���Ƃ��A�d�q�̎��͂��U�d�̂̂悤�ɓ����A�d�q�̉��ɓd�C�o�Ɏq�������ēd������A�d�q�ɂ��^�̓d����Օ����܂�(�^��Օ��ƌ����܂�)�B
�ڂ������Ƃ͏ȗ����܂����A�d�q�E�z�d�q�ΐ����ɂ�����U���U���̌v�Z�����悤�Ƃ���ƁA
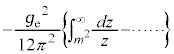 �@(
�@(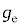 �͌����萔)�@����J
�͌����萔)�@����J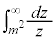 �����U���Ȃ��悤�ɁA�������U�A
�����U���Ȃ��悤�ɁA�������U�A
�Ƃ����āA�J�̒��ɏo�Ă���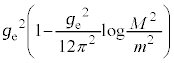 �Ƃ������������̌����萔��2��ł���
�Ƃ������������̌����萔��2��ł���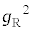 �Œu�������Ė������������邱�Ƃ��l���܂����B���̌v�Z�Z�I�����荞���ƌ����܂��B
�Œu�������Ė������������邱�Ƃ��l���܂����B���̌v�Z�Z�I�����荞���ƌ����܂��B
1947�N�ɕč��̃����ƃN�b�V���́A���f���q�ɂ��āA�f�B���b�N�������������Ək�ނ��Ă��ē����G�l���M�[�����͂��́A2s�O���̃X�s��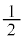 �̏�ԂƁA2p�O���̃X�s��
�̏�ԂƁA2p�O���̃X�s��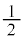 �̏�Ԃ��A���ۂɂ�2s�O���̕����ق�̋͂��ɃG�l���M�[�������Ȃ邱��(�����V�t�g�ƌĂ�Ă��܂�)���}�C�N���g���C���ɂ�蔭�����܂����B���N�A���i��́A���̌��ۂ����荞�Z�@��p���Đ������邱�Ƃɐ������A�Ȍ�A���荞�Z�@���o���_�Ƃ����ʎq�d���͊w���\�z����邱�ƂɂȂ�܂����B���荞�݂́A�d�q��_�ƍl����Ɩ�����ɂȂ��Ă��܂��̂��A�^��Օ��̌��ʂ�g�ݓ��ꂽ���ۂ̊ϑ����ʂ�p���Ė������������邱�Ƃɑ������܂��B�ߎ��Z�@�̂悤�Ɍ�����̂ł����A���荞�݂ɂ���ē���ꂽ�ʎq�d���͊w�̗��_���A�f���q�̎������ʂƖ����̂Ȃ�������^���܂��B����Ȍ�A�l�X�ȑf���q�̗��_���l�Ă���Ă��܂����A�������Ă��闝�_�̑����́u���荞�݁v��O��Ƃ��Ă��āA�W�����_�ƌ����܂��B�W�����_�Ɋ�Â��f���q�̃��f�����W���͌^�ƌ����܂��B
�̏�Ԃ��A���ۂɂ�2s�O���̕����ق�̋͂��ɃG�l���M�[�������Ȃ邱��(�����V�t�g�ƌĂ�Ă��܂�)���}�C�N���g���C���ɂ�蔭�����܂����B���N�A���i��́A���̌��ۂ����荞�Z�@��p���Đ������邱�Ƃɐ������A�Ȍ�A���荞�Z�@���o���_�Ƃ����ʎq�d���͊w���\�z����邱�ƂɂȂ�܂����B���荞�݂́A�d�q��_�ƍl����Ɩ�����ɂȂ��Ă��܂��̂��A�^��Օ��̌��ʂ�g�ݓ��ꂽ���ۂ̊ϑ����ʂ�p���Ė������������邱�Ƃɑ������܂��B�ߎ��Z�@�̂悤�Ɍ�����̂ł����A���荞�݂ɂ���ē���ꂽ�ʎq�d���͊w�̗��_���A�f���q�̎������ʂƖ����̂Ȃ�������^���܂��B����Ȍ�A�l�X�ȑf���q�̗��_���l�Ă���Ă��܂����A�������Ă��闝�_�̑����́u���荞�݁v��O��Ƃ��Ă��āA�W�����_�ƌ����܂��B�W�����_�Ɋ�Â��f���q�̃��f�����W���͌^�ƌ����܂��B
��L�I���œd�q�ُ̈펥�C���[�����g�ɂ��ď����܂������A1917�N�Ƀh�C�c�̃]���}�[�t�F���g�ɂ�蓱�����ꂽ���\���萔�A
��p���āA
�ƕ\����邱�Ƃ��A1948�N�A�č��̃V���E�B���K�[���ʎq�d���͊w��p���ē����܂����B����ȗ��A�ʎq�d���͊w�Ɋ�Â��v�Z���A�X�[�p�[�R���s���[�^�[��p���Đ��x���グ�鎎�݂��Ȃ���Ă��܂����A�����_�ňُ펥�C���[�����g�̎����l�ƌv�Z�l�Ƃ�10���ȏ�̐��x�ň�v���Ă��邻���ł��B���ꂪ�u���荞�݁v�ɂ��v�Z����A���ǁA�W�����_�ւ̐M���ɂȂ����Ă��܂��B
�d�q�����łȂ��A�j�q�ɂ��Ă��A�z�q�̎��ʂ�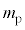 �Ƃ��āA�v�Z��̗z�q(�j�q)�̎��C���[�����g��
�Ƃ��āA�v�Z��̗z�q(�j�q)�̎��C���[�����g��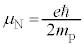 �ƂȂ�̂ł����A�z�q�̎��C���[�����g�̎����l
�ƂȂ�̂ł����A�z�q�̎��C���[�����g�̎����l �Ƃ̔�́A
�Ƃ̔�́A
�ƂȂ�傫������܂��B�d�ׂ��������A�{���[���ł���ׂ������q�̎��C���[�����g�̎����l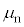 �Ƃ̔�́A
�Ƃ̔�́A
�ƂȂ�A�d�ׂ������Ȃ������q�����C���[�����g�����A�Ƃ����s�v�c�Ȍ��ʂƂȂ�܂��B�������A�z�q�A�����q���ُ펥�C���[�����g�ƌĂ�܂��B�z�q�A�����q�ُ̈펥�C���[�����g�́A�z�q�A�����q���d�ׂ�L��������\���������Ƃ��M�킹�܂��B
���q�j���ŁA�d�ׂ������Ȃ������q�ɂ̓N�[�����͓͂����܂���B�܂��A���f���q�ȊO�̌��q�j���ɂ͐��d�ׂ����z�q����������܂��B�z�q�Ԃɂ̓N�[�����˗͂������͂��Ȃ̂ɁA���q�j���ŕ����̗z�q�A�����q���܂Ƃ܂��Ă���̂ŁA�j�q�ԂɃN�[�����˗͂ɑł����悤�ȋ����͂������Ă���͂��ł��B���̗͂��j���ƌĂ�A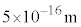 �ȉ��̋����ł͋����˗́A
�ȉ��̋����ł͋����˗́A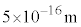 ���z����
���z����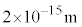 �ȉ��̋����ł͋������͂ɕς��A
�ȉ��̋����ł͋������͂ɕς��A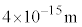 ���炢�ŃN�[�����͂Ɠ����x�A������z����Ɗj�͂͂قƂ�Ǔ������ɃN�[�����݂͂̂ɂȂ�܂��B�j�͂́A�N�[�����͂Ƃ͖��W�ɓ����ɂ߂ē��B�����̒Z���͂ł��B����G���́A���q���d���g��`���ēd���͂�}���悤�ɁA���炩�̗��q���j�͂�}���A�ƍl���A���̗��q�����Ԏq�ƌĂсA1935�N�A���Ԏq�_�\���܂����B���Ԏq�̎��ʂ�m�Ƃ���ƒ��Ԏq�͐Î~�G�l���M�[
���炢�ŃN�[�����͂Ɠ����x�A������z����Ɗj�͂͂قƂ�Ǔ������ɃN�[�����݂͂̂ɂȂ�܂��B�j�͂́A�N�[�����͂Ƃ͖��W�ɓ����ɂ߂ē��B�����̒Z���͂ł��B����G���́A���q���d���g��`���ēd���͂�}���悤�ɁA���炩�̗��q���j�͂�}���A�ƍl���A���̗��q�����Ԏq�ƌĂсA1935�N�A���Ԏq�_�\���܂����B���Ԏq�̎��ʂ�m�Ƃ���ƒ��Ԏq�͐Î~�G�l���M�[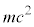 �������܂��A�n�C�[���x���N�̕s�m�萫�����ɂ��A���Ԏq�̎���
�������܂��A�n�C�[���x���N�̕s�m�萫�����ɂ��A���Ԏq�̎���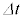 ���A
���A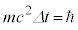 �Ƃ��Č��ς���A���Ԏq��
�Ƃ��Č��ς���A���Ԏq��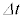 �̊Ԃɍ��X
�̊Ԃɍ��X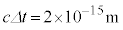 (�j�q�̃T�C�Y)�ړ�����Ƃ��āA
(�j�q�̃T�C�Y)�ړ�����Ƃ��āA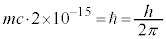 �C�����蒆�Ԏq�̎��ʂ��A
�C�����蒆�Ԏq�̎��ʂ��A
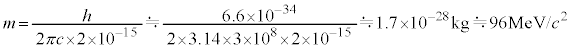 �@(�d�q�̎��ʂ̖�200�{)
�@(�d�q�̎��ʂ̖�200�{)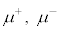 )���F�����̒��ɔ������A���ʂ��d�q��200�{�������̂ł����A�ʗ��q�͊j�q�Ƒ��ݍ�p���������߂��Ă��܂����߁A����̒��Ԏq�ł͂Ȃ��ƌ��_����܂����B�ʗ��q�́A���̓��ߐ��𗘗p���āA�ΎR��s���~�b�h�̓����\���̒����Ɏg���Ă��܂��B�ŋ߂ł́A���̂��N���������������̘F�S�̒����ɂ��g���܂����B
)���F�����̒��ɔ������A���ʂ��d�q��200�{�������̂ł����A�ʗ��q�͊j�q�Ƒ��ݍ�p���������߂��Ă��܂����߁A����̒��Ԏq�ł͂Ȃ��ƌ��_����܂����B�ʗ��q�́A���̓��ߐ��𗘗p���āA�ΎR��s���~�b�h�̓����\���̒����Ɏg���Ă��܂��B�ŋ߂ł́A���̂��N���������������̘F�S�̒����ɂ��g���܂����B
����̒��Ԏq�͒n�\�t�߂ł́A��C���̊j�q�Ƒ��ݍ�p���Ă��܂����߁A���Ԏq���܂މF�������ϑ��ł���悤�ɁA����グ���C���Ɏʐ^�����悹�āA���Ԏq�̍��Ղ�T���܂��B�������Ŏʐ^�����ώ@���邱�Ƃɂ��A1947�N�C�M���X�̃p�E�G��������̒��Ԏq�����܂����B���̂Ƃ��������ꂽ�͓̂d�ׂ�L����Η��q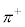 ��
��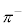 �ŁA���ʂ�
�ŁA���ʂ� (�d�q�̖�300�{)�A������
(�d�q�̖�300�{)�A������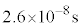 �ŁA�e�X�A
�ŁA�e�X�A
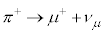 �C
�C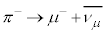
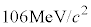 �C����
�C����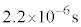 �ŁA
�ŁA
 �C
�C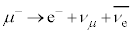
1948�N�ɂ͓d�ׂ������Ȃ�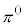 ����������A���ʂ�
����������A���ʂ�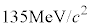 �C������
�C������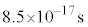 �ŁA2�̌��q�ɕ��܂��B�Ȃ��A�Η��q�̓X�s��0�ŁA��Ԕ��]�ɑ��ĕ�����ς��܂��B
�ŁA2�̌��q�ɕ��܂��B�Ȃ��A�Η��q�̓X�s��0�ŁA��Ԕ��]�ɑ��ĕ�����ς��܂��B
�d���f���q�j�ł̗z�q�A�����q�̌����͂��܂苭���Ȃ�(�����G�l���M�[��������)�A�����q2�ł͂Ȃ����������܂���B�z�q2�A�����q2�̃w���E�����q�j�ł͌����͋����Ȃ�܂��B�j�͂ɂ�錋�����������ݍ�p�ƌ����A����Ɋ֗^���闱�q���n�h�����ƌ����܂����A�j�q���m�̌����ɂ��Ă̓N�H�[�N�ɂ�������҂��ƂɂȂ�܂��B�z�q�ƒ����q�͊j�q�Ƃ��Ď��ʂƓd�ׂ̈Ⴂ�ȊO�͂悭���Ă���̂ŁA�z�q�ƒ����q�헱�q�̈قȂ��Ԃƍl���A���z�I�ȉדd��Ԃ�z�肵���A�C�\�X�s���ƌĂ��p�^���ʂ��l���܂��B�p�^���ʂ�z�������l�����̂Ɠ��l�ɁA�A�C�\�X�s���̑�3����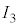 ���l���A�z�q�ł�
���l���A�z�q�ł�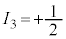 �C�����q�ł�
�C�����q�ł�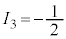 �Ƃ��܂��B�Β��Ԏq�̃A�C�\�X�s����1�ŁA
�Ƃ��܂��B�Β��Ԏq�̃A�C�\�X�s����1�ŁA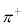 �ł�
�ł�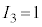 �C
�C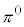 �ł�
�ł�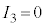 �C
�C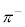 �ł�
�ł�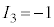 �Ƃ��܂��B�z�q�ƒ����q�͔����Ɏ��ʂ��قȂ�̂ŃA�C�\�X�s���̑Ώ̐��͋ߎ��I�Ώ̐��ƌ����܂��B�n�h�����̑��ݍ�p�ł́A�A�C�\�X�s�����ߎ��I�ɕۑ�����܂��B
�Ƃ��܂��B�z�q�ƒ����q�͔����Ɏ��ʂ��قȂ�̂ŃA�C�\�X�s���̑Ώ̐��͋ߎ��I�Ώ̐��ƌ����܂��B�n�h�����̑��ݍ�p�ł́A�A�C�\�X�s�����ߎ��I�ɕۑ�����܂��B
�f���q(����3)�ɂÂ��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
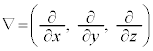 )���{���ƁA���Θ_���l�������������Ƃ��āA
)���{���ƁA���Θ_���l�������������Ƃ��āA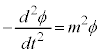 �@����A
�@����A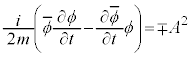
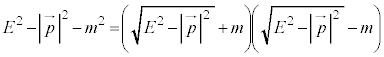 �@����B
�@����B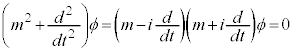 �Ƃ��ĉ����悤�Ȃ��̂ł��B���Θ_�ł́A�h�E�u���C�̊W�����
�Ƃ��ĉ����悤�Ȃ��̂ł��B���Θ_�ł́A�h�E�u���C�̊W�����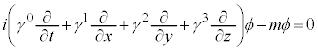 �@����C
�@����C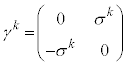 (
(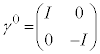 �@(0��2�s2��̗�s��)
�@(0��2�s2��̗�s��)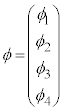 �ƂȂ�܂��B�C�͑��Θ_�I�ȋL�q������ƁA
�ƂȂ�܂��B�C�͑��Θ_�I�ȋL�q������ƁA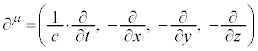 �ł�)�B�܂��A
�ł�)�B�܂��A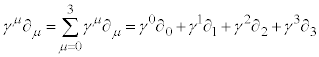 (�㑤�̓Y���Ɖ����̓Y������v�����Ęa���Ƃ邱�Ƃ��k���ƌ����܂�)�̂��Ƃł��B��发�ɂ���ẮA�K���}�s��Ƃ̏k���
(�㑤�̓Y���Ɖ����̓Y������v�����Ęa���Ƃ邱�Ƃ��k���ƌ����܂�)�̂��Ƃł��B��发�ɂ���ẮA�K���}�s��Ƃ̏k���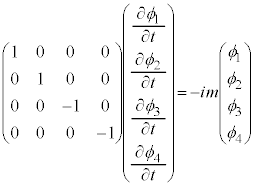
 �C
�C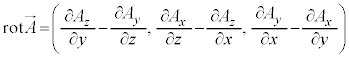
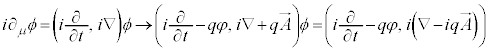
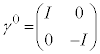 �������āA
�������āA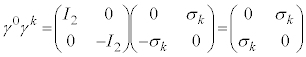 (
(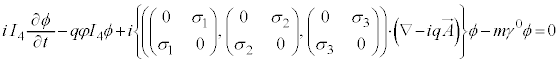
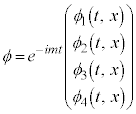 �C
�C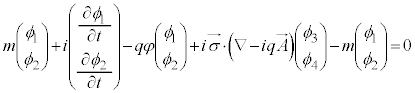 �@����E
�@����E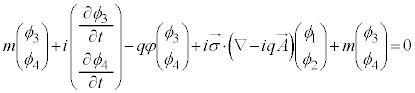 �@����F
�@����F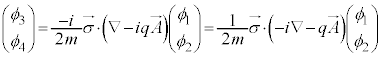
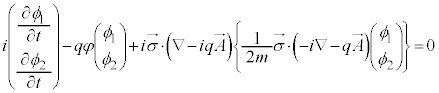
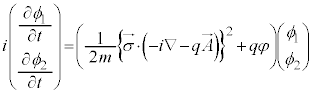 �@����G
�@����G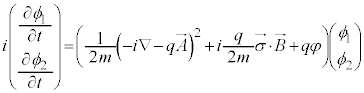 �@����H
�@����H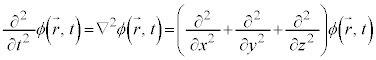
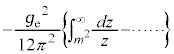 �@(
�@(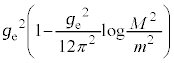 �Ƃ������������̌����萔��2��ł���
�Ƃ������������̌����萔��2��ł���