�f���q
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���݁A���G�l���M�[�������p����������F�����̊ϑ��ɂ��A�����̑f���q�̑��݂��킩���Ă��܂����A���̂����ōł��悭�m���Ă���f���q�͓d�q�ł��B�d�q���דd���q�Ƃ��Ĉ����A��d�ׂ����߂��̂�J.J.�g���\���ł�(���q���Q��)���A1895�N����10�N�ɓn��I�����_�̃��[�����c���A�}�N�X�E�F���̓d���C�w�Ɋ�Â��ēd�q���l�@���܂����B�ނ́A���q�͉דd���q����ł��Ă���Ǝ咣���A��q�̃[�[�}�������������[�[�}������(�i�g���E�������ꒆ�ɒu���ƁA�i�g���E������o�Ă�����̂���D���̃X�y�N�g����2�{�ȏ�ɕ������)���l�@���AJ.J.�g���\���Ƃ͕ʌɓd�q�̔�d�ׂ����߂܂����B�܂��A�F���̐�ΐÎ~�n�G�[�e���̔ے�ƂȂ����A�}�C�P���\���E���[���[�̎���(���g���Q��)�ɂ��āA���ΓI�Ɉړ�������W�n�̊Ԃ̕ϊ�����(���[�����c�ϊ��ƌ����܂�)���A�^�����镨�͉̂^�������ɏk�ށA�^�����鎞�v�͒x���A�Ƃ������[�����c���k�ƌĂ����߂�20���I�����ɔ��\���܂����B���̍l�����́A��ɃA�C���V���^�C���ɂ���đ��ΐ����_�ɂ܂Ƃ߂��邱�ƂɂȂ�܂��B
���[�����c�͓d�q��d�ׂ�L���鋅�̂ƍl���܂����B���[�����c�ɂ��ƁA�d��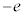 �����דd���q�̋��̂̔��a��r�Ƃ���ƁA���̂̕\�ʂɒu���ꂽ�d��e�̈ʒu�G�l���M�[(�d�����Q��)�́A�N�[�������̔��萔��k�Ƃ��āA
�����דd���q�̋��̂̔��a��r�Ƃ���ƁA���̂̕\�ʂɒu���ꂽ�d��e�̈ʒu�G�l���M�[(�d�����Q��)�́A�N�[�������̔��萔��k�Ƃ��āA
�ł��B�דd���q�̎��ʂ�m�C������c�Ƃ���ƁA���̉דd���q�����Î~�G�l���M�[(���q�j���Q��)��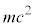 �C�����d�ׂ��Î~���Ă���Ƃ��āA�N�[�����͂̈ʒu�G�l���M�[�̐�Βl�Ɠ��l����ƁA�^��̗U�d���A��������
�C�����d�ׂ��Î~���Ă���Ƃ��āA�N�[�����͂̈ʒu�G�l���M�[�̐�Βl�Ɠ��l����ƁA�^��̗U�d���A��������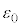 �C
�C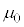 �Ƃ��āA
�Ƃ��āA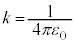 �C
�C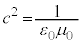 ���A
���A
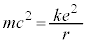 �@��
�@�� 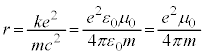
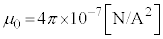 �Ƃ��A�܂��d�q�̒l�A
�Ƃ��A�܂��d�q�̒l�A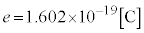 �C
�C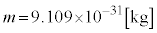 ��p����ƁA
��p����ƁA
���̒l���ÓT�d�q���a�ƌ����܂��B�f���q�_�ȑO�́A���̒l���d�q�̔��a�ƍl�����Ă��܂����B
�ł����A���a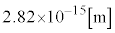 �̋������̓��ɓd�ׂ��������߂��Ă���A�Ƃ������ƂɂȂ�ƁA�ǂ̂悤�ɓd�ׂ����z���Ă���̂��H�A���I�ɋ��̂̕\�ʂɕ��z���Ă���̂��H���邢�́A���̒��S1�_�ɏW�����đ��݂��Ă���̂��H�Ƃ�����肪�����܂��B�d�ׂ����̕\�ʂɕ��z����Ƃ������ƂɂȂ�ƁA�����̊Ԃɓ����N�[�����͂̐˗͂͐��܂������̂ɂȂ�A���̐˗͂ɑł������ēd�ׂ�d�q���ɂ܂Ƃ߂Ă���͉͂��Ȃ̂��A�Ƃ����^�₪�����܂��B�t�ɋ��̒��S1�_�ɏW�����đ��݂��Ă���Ƃ���ƁA���̓_�ŃN�[�����͂̈ʒu�G�l���M�[�̐�Βl�͖�����ɂȂ��Ă��܂��܂��B�����ŁA1947�N�ɒ��i�U��Y�炪�\�z�����u���肱�ݗ��_�v�ɂ���Ė�����̍��������A�f���q�_�ł́A�d�q�A���̑��̑f���q�̑傫����0�Ƃ��čl���܂��B
�̋������̓��ɓd�ׂ��������߂��Ă���A�Ƃ������ƂɂȂ�ƁA�ǂ̂悤�ɓd�ׂ����z���Ă���̂��H�A���I�ɋ��̂̕\�ʂɕ��z���Ă���̂��H���邢�́A���̒��S1�_�ɏW�����đ��݂��Ă���̂��H�Ƃ�����肪�����܂��B�d�ׂ����̕\�ʂɕ��z����Ƃ������ƂɂȂ�ƁA�����̊Ԃɓ����N�[�����͂̐˗͂͐��܂������̂ɂȂ�A���̐˗͂ɑł������ēd�ׂ�d�q���ɂ܂Ƃ߂Ă���͉͂��Ȃ̂��A�Ƃ����^�₪�����܂��B�t�ɋ��̒��S1�_�ɏW�����đ��݂��Ă���Ƃ���ƁA���̓_�ŃN�[�����͂̈ʒu�G�l���M�[�̐�Βl�͖�����ɂȂ��Ă��܂��܂��B�����ŁA1947�N�ɒ��i�U��Y�炪�\�z�����u���肱�ݗ��_�v�ɂ���Ė�����̍��������A�f���q�_�ł́A�d�q�A���̑��̑f���q�̑傫����0�Ƃ��čl���܂��B
1909�N�ɃK�C�K�[�ƃ}�[�X�f�����s���������ŁA���̔�����α���Ă�ƁA�قƂ�ǂ�α�����f�ʂ肷�钆�ɑ傫������������̂����邱�Ƃ���������܂����B���̎������w���������U�t�H�[�h�́A1911�N�ɁA���d�ׂ�L���錴�q�j�����q�̒��S�ɏW�����đ��݂��A���̎��͂�d�q������A�Ƃ������q���f���\���܂����B�������A���̌�A���U�t�H�[�h���g�ŗz�q�����A����ɂ͓��ʑ̂̑��݂�������邽�߂ɒ����q�̑��݂�\������Ɏ����āA���q�j�́A�z�q�ƒ����q����\�������Ƃ����\���������Ƃ��킩���Ă��܂����B
z�������ω����鎥��̒��ő���v��z���̎���ɉ~�^������דd���q�������C���[�����g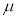 �ׂ܂��Bz�����ӂŋǏ��I�ȉ~�����W�n
�ׂ܂��Bz�����ӂŋǏ��I�ȉ~�����W�n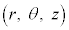 ���Ƃ莥�����x�̊e����������
���Ƃ莥�����x�̊e����������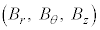 �Ƃ��āA
�Ƃ��āA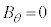 �C
�C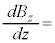 ���ƍl����ƁA
���ƍl����ƁA
��������ɉדd���q����͂́A�@�C�A���A
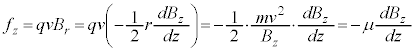 �@����B
�@����B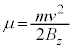 �́A�@���A
�́A�@���A
�ƌ���ƁA�דd���q������v�Œ���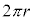 �̉~����������鎞��
�̉~����������鎞��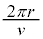 �œd��q�����������̂�d���ƌ��Ȃ��ƁA
�œd��q�����������̂�d���ƌ��Ȃ��ƁA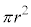 �͉~�̖ʐςȂ̂ŁAμ�́A���ar�̉~�O��������דd���q�̍�����C���[�����g�ł��B�{�[�A�̌��q�͌^�̏ꍇ(�d�ׁFe�C���C���[�����g�F
�͉~�̖ʐςȂ̂ŁAμ�́A���ar�̉~�O��������דd���q�̍�����C���[�����g�ł��B�{�[�A�̌��q�͌^�̏ꍇ(�d�ׁFe�C���C���[�����g�F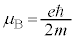 )�ɂ́A
)�ɂ́A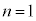 �̂Ƃ����{�[�A�̗ʎq�����F
�̂Ƃ����{�[�A�̗ʎq�����F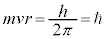 ���A
���A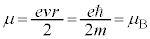 �ƂȂ�܂��B
�ƂȂ�܂��B
���{�[�A���q�ƌ����܂��B
1922�N�̃V���e�����E�Q�����b�n�̎����ŁA��̌��q�r�[������l�łȂ�����ɒʂ��Ǝ��������2�ɕ��ċȂ���(���[�����c�͂ɂ����̂Ȃ玥��Ɛ����ȕ����ɋȂ���͂�)���Ƃ���������܂����B��������ɋȂ���̂͋⌴�q���̓d�q�����C���[�����g(�����~�d��)�������Ă��Ă��ꂪ��������ɇB��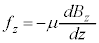 �̗͂��邩��Ɛ�������܂����B�⌴�q��47�̓d�q�������Ă��܂����AK�k�AL�k�AM�k�͕k�AN�k��4s�O���A4p�O���A4d�O���������ŁA�����܂łœd�q46�̊p�^���ʂ̘a�̓[���ɂȂ�A5s�O���̓d�q1������̉e�����܂��B�⌴�q�r�[���̕���́A5s�O���̓d�q1�̊p�^���ʂ�2�ʂ�̒l��������ł͂Ȃ����A�ƍl�����܂���(�ʎq�͊w�̊�b(����3)���Q��)�B
�̗͂��邩��Ɛ�������܂����B�⌴�q��47�̓d�q�������Ă��܂����AK�k�AL�k�AM�k�͕k�AN�k��4s�O���A4p�O���A4d�O���������ŁA�����܂łœd�q46�̊p�^���ʂ̘a�̓[���ɂȂ�A5s�O���̓d�q1������̉e�����܂��B�⌴�q�r�[���̕���́A5s�O���̓d�q1�̊p�^���ʂ�2�ʂ�̒l��������ł͂Ȃ����A�ƍl�����܂���(�ʎq�͊w�̊�b(����3)���Q��)�B
�O�q�̃[�[�}�����ʂ��A���[�����c�͌ÓT�_�Ɋ�Â��Đ��������̂ł����A�ʎq�͊w�ɂ���āA�i�g���E���̏o�����̂���D���́A�i�g���E�����q�����d�q��3p��3s�̑J�ڂŔ���������q�ɂ����̂Ƃ킩��܂����B�i�g���E����K�k�AL�k���k��3s�O���̓d�q�����f�̎�ʎq��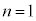 �̓d�q�̂悤�Ȃӂ�܂������܂��B����D���́AD1�CD2��2�{�̃X�y�N�g���ɕ��Ă���̂ł����A1925�N�I�����_�̃E�[�����x�b�N�ƃS�[�Y�~�b�g(���_���n�̂��ߌ�ɕč��ɋA��)���A�i�g���E����3p�́A�d�q�̎��](�����͓d�q�͑傫�������ƍl�����Ă��܂���)�ɂ��p�^���ʂ̈Ⴂ�ɂ���ăG�l���M�[���ʂ�2�ɕ�����X�y�N�g��������A�Ɛ������܂����B�V���e�����E�Q�����b�n�̎����̋⌴�q�r�[���̕���̗��R�����l�ɐ����ł��܂��B���q�j���ŕ��ʗʎq���Ō��܂�p�^���ʂ��O���p�^���ʁA�܂��A�d�q1���ŗL�Ɏ��p�^���ʂ��X�s���p�^���ʁA���邢�͒P�ɃX�s���ƌ����܂��B�d�q�̋O���p�^���ʂɂ�鎥�ꂪ�d�q�̃X�s���ɉe����^����ȂǁA�p�^���ʓ��m�̑��ݍ�p�A�܂�������������Ƃ��̎���Ƃ̑��ݍ�p�ɂ��A�X�y�N�g�������G�ɕ�����邱�Ƃ��������Ă��܂��B
�̓d�q�̂悤�Ȃӂ�܂������܂��B����D���́AD1�CD2��2�{�̃X�y�N�g���ɕ��Ă���̂ł����A1925�N�I�����_�̃E�[�����x�b�N�ƃS�[�Y�~�b�g(���_���n�̂��ߌ�ɕč��ɋA��)���A�i�g���E����3p�́A�d�q�̎��](�����͓d�q�͑傫�������ƍl�����Ă��܂���)�ɂ��p�^���ʂ̈Ⴂ�ɂ���ăG�l���M�[���ʂ�2�ɕ�����X�y�N�g��������A�Ɛ������܂����B�V���e�����E�Q�����b�n�̎����̋⌴�q�r�[���̕���̗��R�����l�ɐ����ł��܂��B���q�j���ŕ��ʗʎq���Ō��܂�p�^���ʂ��O���p�^���ʁA�܂��A�d�q1���ŗL�Ɏ��p�^���ʂ��X�s���p�^���ʁA���邢�͒P�ɃX�s���ƌ����܂��B�d�q�̋O���p�^���ʂɂ�鎥�ꂪ�d�q�̃X�s���ɉe����^����ȂǁA�p�^���ʓ��m�̑��ݍ�p�A�܂�������������Ƃ��̎���Ƃ̑��ݍ�p�ɂ��A�X�y�N�g�������G�ɕ�����邱�Ƃ��������Ă��܂��B
���̍��ځu�f���q�v�ł́A�f���q�̗��_�E�����ɂ��Č��čs���܂����A�f���q�̌��o�ɂ́A1897�N�ɃE�B���\������������������p���܂��B�ߖO�a�����C�̒����דd���q���ʉ߂���ƋC�̕��q���C�I�������܂��B�C�I�������ꂽ�C�̕��q�̖����̗�����邱�Ƃɂ���đf���q�̔�Ղ�m�邱�Ƃ��ł��܂��B�C�I�����j�ɂ��ċC�A���ł���Ƃ��ɂ́A�C�A�̗�����邱�Ƃɂ���Ĕ�Ղ��킩��܂��B����͖A���ƌ����A1952�N�O���[�U�[���������܂����B�j���[�g���m�͓d�ׂ������Ȃ����ߖ����ł͔�Ղ����o�ł��܂���B�j���[�g���m�������ƏՓ˂����ۂɂł���C�A�ɂ��ԐړI�ɔ�Ղׂ܂��B���_���̃J�~�I�J���f�ł́A�j���[�g���m���d�q�ƏՓ˂������Ƃɓd�q�����˂���`�F�����R�t�������d�q���{�ǂŌ��o���܂��B�f���q�̌��o�ɂ́A���ɂ����d����v�������H�v����Ă��܂��B���q�̏ꍇ�ɂ́A�u���������ăV���`���[�V�����J�E���^�[�Ō��o���܂��B�d�ׂ����f���q�ł́A���������������[�����c�����ĉ~�^������̂ŁA�~�^���̌�������d�ׂ̐����ׁA�~�^���̉�]���a����d�ׂ̑傫���A���q�̉^���ʂ����߂܂��B�d�ׂ̑��x���傫���ꍇ�ɂ͑��Θ_�I���ʂ��l������K�v������܂��B�f���q����Ղ���������Ԃ�������Δ�Ղ̒������瑬����������A�f���q�̎��ʂ����߂��܂��B
�z�q���m���Փ˂�����ꍇ�ɂ̓N�[�����͂ɑł����G�l���M�[��z�q�ɗ^����K�v������܂��B�܂��A���G�l���M�[�̑f���q��������ꍇ�Ȃǂɂ��A����ȉ����킪�K�v�ɂȂ�܂��B����ȉדd���q�̏ꍇ�ɂ́A�d��������ĉ������܂��B���d���邽�߂ɁA�R�b�N�N���t�g�E�E�H���g����H(���啨��'11�N[2])�Ȃǂ��g���܂��B
������ɂ́A���`������Ɖ~�`�������2�ʂ肪�l�����܂��B
���`������ł́A�݂��ɐ≏���ꂽ���̓�����ɐ��������ׁA�e�d�ɂɍ����g�d���������A���������ʉ߂���דd���q�Ɠ��������Ŋe�d�ɂ̓d�����ړ������āA�דd���q���������܂��B
�~�`������́A�T�C�N���g�����ƃV���N���g������2�ʂ肠��܂��B
�T�C�N���g�����́A�������ɂȂ��Ă��锼�~�`�̓d�ɂ��Ԋu����2���킹�ĉ~�`�ɂȂ�悤�ɐݒu���A2�̓d�ɊԂɍ����g�d���������A���̉~�Ɛ����Ɏ���������܂��B�~�̒��S��������דd���q���~�`�̋��ɓ�������ƁA2�̔��~�`�̓d�ɂ̊Ԍ�������ʉ߂���Ƃ��ɉדd���q������(�דd���q�����������דd���q�Ɠ������d�ʁA�דd���q���N�����鑤���ٕ����d�ʂƂȂ�d���ʼn������܂�)����A�דd���q�̑������傫���Ȃ邽�тɉ~�^���̔��a���傫���Ȃ�A�K�v�ȃG�l���M�[�܂ʼn������ꂽ�Ƃ���ŁA�~�̊O�Ɏ��o���܂��B�������xB�̈�l�Ȏ��ꒆ�𑬂�v�ŁA���ar�̉~�^������דd���qq���������鎞�Ԃ͔��a�Ɉˑ��������(�^���������F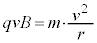 ���A�������鎞�Ԃ�
���A�������鎞�Ԃ�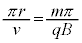 )�Ȃ̂ŁA���̎��g���̍����g�d���ʼn����ł��܂��B
)�Ȃ̂ŁA���̎��g���̍����g�d���ʼn����ł��܂��B
�V���N���g�����́A�����������דd���q������^������o�H�ɉ����āA�^���������Ȃ��鎥������d�������t���������ƁA���q�����������邽�߂̓d����������Ԍ������Ƃ�݂��܂��B���q�͂��炩���ߕʂ̐��`������ʼn������đ��u���ɓ��˂����܂��B�Ԍ������ʼn���������̂ɏ]���ēd���̎�����������A�דd���q���������������^������悤�ɐ��䂵�A�K�v�ȃG�l���M�[�܂ʼn������ꂽ��ɁA�דd���q�̃r�[�����O���Ɏ��o���܂��B����O��������悤�ɉ�����邱�Ƃɂ��A�傫�ȃG�l���M�[�̗��q�邱�Ƃ��ł��܂��B
���q��W�I�ɓ��ĂĎU��������Ƃ��A�P�ʖʐϓ����薈�bN�̗��q����˂�����ƁA�pθ�̕��������̊p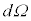 ���ɎU������闱�q���b
���ɎU������闱�q���b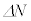 �Ƃ��āA
�Ƃ��āA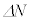 ��
��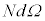 �ɔ�Ⴗ��̂ŁA
�ɔ�Ⴗ��̂ŁA
�ƂȂ�܂��B�����ŁA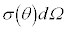 �͖ʐς̎����������Ă���
�͖ʐς̎����������Ă���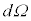 �̒��ɗ��q���U��������W�I�̖ʐς�\���ƍl�����܂��B���������f�ʐςƌ����A�S���̊p�ɓn���Đϕ�����ƁA
�̒��ɗ��q���U��������W�I�̖ʐς�\���ƍl�����܂��B���������f�ʐςƌ����A�S���̊p�ɓn���Đϕ�����ƁA
�́A�U������m����^���A�U������闱�q�̑����͖��b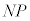 �ł��B����P��S�f�ʐςƌ����܂��B�܂��A�pθ���U���p�ƌ����܂��B���q���m�̏Փ˂͂���ۂɂ́A�U���f�ʐρA�U���p�ׂ邱�ƂɂȂ�܂��B
�ł��B����P��S�f�ʐςƌ����܂��B�܂��A�pθ���U���p�ƌ����܂��B���q���m�̏Փ˂͂���ۂɂ́A�U���f�ʐρA�U���p�ׂ邱�ƂɂȂ�܂��B
1926�N�ɃI�[�X�g���A�̃V�����[�f�B���K�[���A�h�E�u���C�̕����g�̒�Ă��āA�g������������A�����g����闱�q���]���Θ_�I�ȃV�����[�f�B���K�[�������o���܂���(�ʎq�͊w�̊�b���Q��)�B���̕������̉�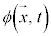 �́A���q�̑��݊m���̔g��\���A
�́A���q�̑��݊m���̔g��\���A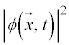 ���m�����x���ł���Ɖ��߂���܂����B
���m�����x���ł���Ɖ��߂���܂����B
�����ŁA�p�^�����ɂ��čl���܂��B�ʒu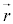 �ɂ��镨�̂��^����
�ɂ��镨�̂��^����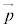 �����Ƃ��A���̂̊p�^���ʂ́A
�����Ƃ��A���̂̊p�^���ʂ́A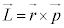 (�~���O���ł�)�ŗ^�����܂��B�p�^���ʂ���Ԃ̕ϊ��Ŏ�e�����l�������̂ł����A�܂��A���ʂ���b��i�߂܂��B���ʏ�̃x�N�g���̒�����ς��Ȃ�(
(�~���O���ł�)�ŗ^�����܂��B�p�^���ʂ���Ԃ̕ϊ��Ŏ�e�����l�������̂ł����A�܂��A���ʂ���b��i�߂܂��B���ʏ�̃x�N�g���̒�����ς��Ȃ�(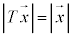 )�ϊ�T�́Aθ���p�Ƃ��āA�s��
)�ϊ�T�́Aθ���p�Ƃ��āA�s��
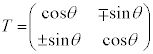 �@(��������)�@����C
�@(��������)�@����C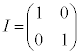 �Ƃ��āA�����s��́A
�Ƃ��āA�����s��́A
���A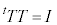 (
(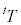 �͍s��T�̓]�u�s��A�܂�A
�͍s��T�̓]�u�s��A�܂�A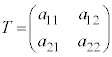 �̂Ƃ�
�̂Ƃ�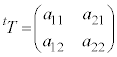 �C�s�����Q��)�Ƃ��������������܂��B�s��
�C�s�����Q��)�Ƃ��������������܂��B�s��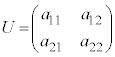 �̐����f���Ƃ���ꍇ�A
�̐����f���Ƃ���ꍇ�A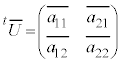 �ł����A
�ł����A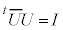 �ƂȂ�Ƃ��A�s��U�̕\���ϊ��͕��f���𐬕��Ƃ���x�N�g���̑傫����ς��܂���(
�ƂȂ�Ƃ��A�s��U�̕\���ϊ��͕��f���𐬕��Ƃ���x�N�g���̑傫����ς��܂���(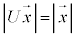 )�B���̂Ƃ��A�ϊ������j�^���ϊ��A�s��U�����j�^���s���ƌ����܂��B�����s��͐����������ł��郆�j�^���s��ƌ������Ƃ��ł��܂��B
)�B���̂Ƃ��A�ϊ������j�^���ϊ��A�s��U�����j�^���s���ƌ����܂��B�����s��͐����������ł��郆�j�^���s��ƌ������Ƃ��ł��܂��B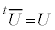 �ƂȂ�s����G���~�[�g�s���ƌ����܂��B�ʎq�͊w�ŕ����ʂ����߂鉉�Z�q��A�C�ŗL�l��a�C�ŗL�x�N�g����
�ƂȂ�s����G���~�[�g�s���ƌ����܂��B�ʎq�͊w�ŕ����ʂ����߂鉉�Z�q��A�C�ŗL�l��a�C�ŗL�x�N�g����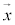 �Ƃ��āA
�Ƃ��āA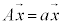 �ƂȂ�܂����AA�̓G���~�[�g�s���a�͎����ł��B
�ƂȂ�܂����AA�̓G���~�[�g�s���a�͎����ł��B
����ϊ��S�̂��Q�����܂��B�u�W��G�����Z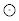 �ɂ��ČQ�����v�Ƃ����̂́A
�ɂ��ČQ�����v�Ƃ����̂́A
�C�ӂ�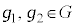 �ɂ���
�ɂ���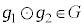
�C�ӂ�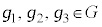 �ɂ���
�ɂ���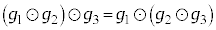
�Ƃ��������������Ƃ������܂��Bθ��C�ӂ̎����Ƃ���Ƃ��̒����s��T�S�̂�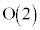 �ƕ\���܂��B�s��̐ςɂ��āA
�ƕ\���܂��B�s��̐ςɂ��āA
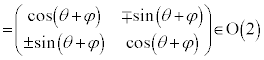 �@(��������)
�@(��������)�C�ӂ�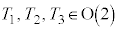 �ɂ���
�ɂ���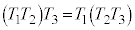
�C�ӂ�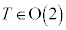 �ɂ���
�ɂ���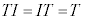
�ƂȂ�A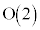 �͌Q�����A2���������Q�ƌ����܂��B
�͌Q�����A2���������Q�ƌ����܂��B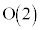 �ɂ�2�^�C�v����A
�ɂ�2�^�C�v����A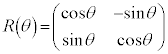 �Ƃ����^�C�v��
�Ƃ����^�C�v��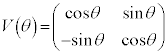 �Ƃ����^�C�v�ł��B
�Ƃ����^�C�v�ł��B
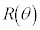 �͌��_�̉��̊pθ�̉�]�ړ�(��]�ϊ�)�C
�͌��_�̉��̊pθ�̉�]�ړ�(��]�ϊ�)�C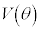 �͒���
�͒���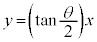 �Ɋւ���Ώ̈ړ�(���f�ϊ��A���])��\���܂�(1���ϊ�(����2)���Q��)�B���҂́A�s���̒l���قȂ�A
�Ɋւ���Ώ̈ړ�(���f�ϊ��A���])��\���܂�(1���ϊ�(����2)���Q��)�B���҂́A�s���̒l���قȂ�A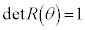 �C
�C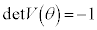 �ł��B
�ł��B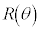 �̑S�̂ł��Q�����̂ł����A�����2�������꒼���Q�ƌ���
�̑S�̂ł��Q�����̂ł����A�����2�������꒼���Q�ƌ���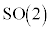 �ƕ\���܂��B2�����̉�]���������̂ɁA��Βl1�̕��f��
�ƕ\���܂��B2�����̉�]���������̂ɁA��Βl1�̕��f��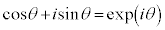 ������܂��B����͌����1�����̃��j�^���s��Ƃ���������̂ŁA
������܂��B����͌����1�����̃��j�^���s��Ƃ���������̂ŁA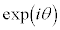 �̕\���ϊ��S�̂͌Q
�̕\���ϊ��S�̂͌Q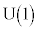 ���Ȃ��A�����1�������j�^���Q�ƌ����܂��B
���Ȃ��A�����1�������j�^���Q�ƌ����܂��B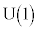 �̗v�f��
�̗v�f��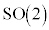 �̗v�f�������I�ɓ�����]��\���܂��B���̎������A
�̗v�f�������I�ɓ�����]��\���܂��B���̎������A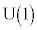 ��
��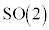 �͓��^�ł���A�ƌ����܂��B�s��͈�ʂɁA2�̍s��A�CB�ɂ��āA
�͓��^�ł���A�ƌ����܂��B�s��͈�ʂɁA2�̍s��A�CB�ɂ��āA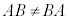 �ł����A
�ł����A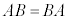 �ƂȂ�Ƃ����ł���ƌ����܂��B�Q�̗v�f���m�̐ς����ł���Ƃ��A���Q�A�܂��̓A�[�x���Q�ƌ����܂��B2�������ꃆ�j�^���Q
�ƂȂ�Ƃ����ł���ƌ����܂��B�Q�̗v�f���m�̐ς����ł���Ƃ��A���Q�A�܂��̓A�[�x���Q�ƌ����܂��B2�������ꃆ�j�^���Q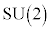 �ł́A
�ł́A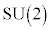 �̌�U�́A
�̌�U�́A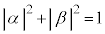 �Ƃ��āA
�Ƃ��āA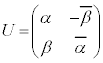 �Ə����܂��B
�Ə����܂��B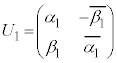 �C
�C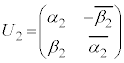 �C
�C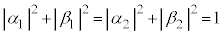 �Ƃ��āA
�Ƃ��āA
���A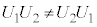 �ł����āA
�ł����āA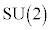 �͔���Q�ł��B
�͔���Q�ł��B
3�����̏ꍇ�ɂ��Ă��A�܂�z���̂܂��̊pϕ�̉�]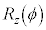 ���s���A����y���̂܂��̊pθ�̉�]
���s���A����y���̂܂��̊pθ�̉�]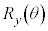 ���s���A�Ō��z���̂܂��̊pφ�̉�]
���s���A�Ō��z���̂܂��̊pφ�̉�]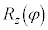 ������������
������������
�̑S�̂ŋ�Ԃ̂������]��\���̂ł����A�Q�����܂��B�s��1�ɂȂ�̂ŁA���̌Q��3�������꒼���Q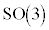 �ł��B��]�ϊ��̌Q�A
�ł��B��]�ϊ��̌Q�A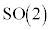 �C
�C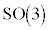 �͉��Q�ł��B�p�^���ʂ̑傫����2��
�͉��Q�ł��B�p�^���ʂ̑傫����2��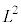 �͋�ԉ�]�ŕω������A�܂�
�͋�ԉ�]�ŕω������A�܂�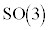 �ɑ�����ϊ����Ă��ω����܂���B���̎������A
�ɑ�����ϊ����Ă��ω����܂���B���̎������A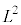 ��
��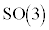 �Ώ̐������A�Ƃ��������������܂��B
�Ώ̐������A�Ƃ��������������܂��B
�p�^����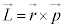 �ɘb��߂��A
�ɘb��߂��A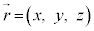 �C
�C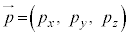 �Ƃ��Ċp�^����
�Ƃ��Ċp�^����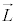 �̐����́A
�̐����́A
�V�����[�f�B���K�[�����������Ƃ��̋K���F
���{���ƁA
�ƂȂ�܂��B�ʎq�͊w�ł́A���Z�q�̌����W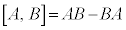 ���l���܂��B
���l���܂��B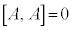 �C
�C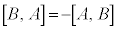 �ł��B�Ⴆ�ΌÓT�_�ł�x���W�Ɖ^���ʂ�x�����ƂŁA
�ł��B�Ⴆ�ΌÓT�_�ł�x���W�Ɖ^���ʂ�x�����ƂŁA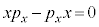 �ł����A�ʎq�͊w�ł͕K�����������͂Ȃ�܂���Bx���W���Z�q�Ɖ^���ʂ�x�������Z�q�ƂŁA�����W�ׂ�(���Z�q�̌����W�Ȃ̂Ŋ�ϕ�ɂ����Ē��ׂ܂�)�ƁA
�ł����A�ʎq�͊w�ł͕K�����������͂Ȃ�܂���Bx���W���Z�q�Ɖ^���ʂ�x�������Z�q�ƂŁA�����W�ׂ�(���Z�q�̌����W�Ȃ̂Ŋ�ϕ�ɂ����Ē��ׂ܂�)�ƁA
�Ȃǂ��A
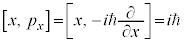 �C
�C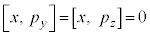
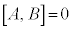 �ɂȂ�Ƃ��A���Z�qA��B�͉�(
�ɂȂ�Ƃ��A���Z�qA��B�͉�(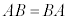 )�ł���ƌ����܂��Bx��
)�ł���ƌ����܂��Bx��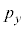 �C
�C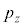 �͉�(
�͉�(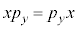 �C
�C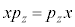 )�ł��B���Z�qA��B�����ł���Ƃ��AA��B�͓����ŗL��������������A��B���ɑ���ł��܂��B
)�ł��B���Z�qA��B�����ł���Ƃ��AA��B�͓����ŗL��������������A��B���ɑ���ł��܂��B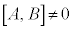 �̂Ƃ�(
�̂Ƃ�(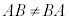 )�͓����ɂ͑���ł����A�Ⴆ�Ax��
)�͓����ɂ͑���ł����A�Ⴆ�Ax��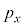 �͓����ɂ͑���ł����A�n�C�[���x���N�̕s�m�萫�����F
�͓����ɂ͑���ł����A�n�C�[���x���N�̕s�m�萫�����F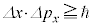 ���������܂��B
���������܂��B
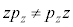 �C
�C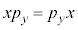 �C
�C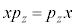 �C
�C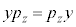 �C
�C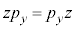 �ɒ��ӂ��āA
�ɒ��ӂ��āA
�܂��A
�ƇD��p���āA
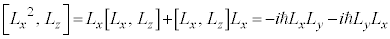 �@����E
�@����E
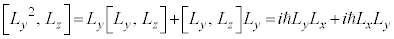 �@����F
�@����F
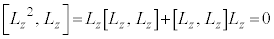 �@����G
�@����G
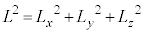 �C�E�{�F�{�G���A
�C�E�{�F�{�G���A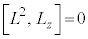
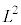 ��
��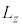 �͌����\�œ����ŗL���������܂��B�V�����[�f�B���K�[������������(�ʎq�͊w�̊�b(����3)���Q��)�ƁA�p���x�̑傫����2��
�͌����\�œ����ŗL���������܂��B�V�����[�f�B���K�[������������(�ʎq�͊w�̊�b(����3)���Q��)�ƁA�p���x�̑傫����2��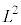 �͌ŗL�l
�͌ŗL�l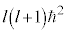 (l�͕��ʗʎq���ƌĂ�Ă��܂��B��ʎq����n�Ƃ��āA
(l�͕��ʗʎq���ƌĂ�Ă��܂��B��ʎq����n�Ƃ��āA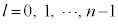 )�������܂��B
)�������܂��B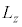 �̌ŗL�l��
�̌ŗL�l��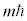 (m�͎��C�ʎq���ƌĂ�Ă��܂��B
(m�͎��C�ʎq���ƌĂ�Ă��܂��B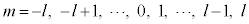 )�ƂȂ�܂��B
)�ƂȂ�܂��B
���܂ŏ����Ă����p�^����L�͋O���p�^���ʂƌĂ�Ă�����̂ł��B���̋O���p�^���ʂɂ�鎥��̉e�����l������ƁA�d�q�ŗL�̃X�s���p�^���ʂƂ̊Ԃɑ��ݍ�p������A������܂߂ăV�����[�f�B���K�[�������������ƁA�p�^���ʂ̌ŗL�l���A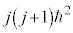 (
(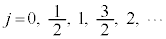 )�ƂȂ�܂��B�O���p�^���ʂ����̂Ƃ��Ɣ�ׂāAj��
)�ƂȂ�܂��B�O���p�^���ʂ����̂Ƃ��Ɣ�ׂāAj�� �̊�{�ɂȂ�ꍇ���o�Ă��܂��B����͓d�q�ŗL�̃X�s���ɂ��e���ł��B�d�q�̃X�s���p�^���ʂ̌ŗL�l��
�̊�{�ɂȂ�ꍇ���o�Ă��܂��B����͓d�q�ŗL�̃X�s���ɂ��e���ł��B�d�q�̃X�s���p�^���ʂ̌ŗL�l��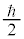 �C
�C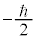 ��2�ʂ�̒l(�d�q�̓X�s��
��2�ʂ�̒l(�d�q�̓X�s��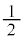 �����A�Ƃ��������������܂�)�����A���ꂪ�O���p�^���ʂƍ�������āAj�����[�Ȓl�����悤�ɂȂ�܂��B�X�s����\���̂ɁA�ŗL�l
�����A�Ƃ��������������܂�)�����A���ꂪ�O���p�^���ʂƍ�������āAj�����[�Ȓl�����悤�ɂȂ�܂��B�X�s����\���̂ɁA�ŗL�l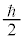 �C
�C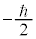 �ɉ����āA
�ɉ����āA
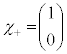 �C
�C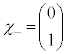
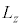 �Ɠ��l�ɁA�X�s���p�^����z�������Z�q
�Ɠ��l�ɁA�X�s���p�^����z�������Z�q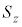 ���ŗL�l
���ŗL�l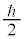 �C
�C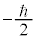 �̏�Ԃ�\���悤�ɁA
�̏�Ԃ�\���悤�ɁA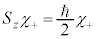 �C
�C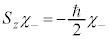 �Ƃ���ƁA
�Ƃ���ƁA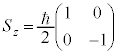 �Ƃ���悢���Ƃ�������܂��B
�Ƃ���悢���Ƃ�������܂��B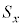 �C
�C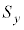 �C
�C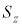 ���p�^���ʉ��Z�q
���p�^���ʉ��Z�q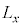 �C
�C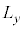 �C
�C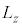 �̌����W�D�Ɠ��l�̊W�����悤�ɂ��邽�߂ɂ́A
�̌����W�D�Ɠ��l�̊W�����悤�ɂ��邽�߂ɂ́A
�Ƃ��āA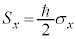 �C
�C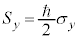 �C
�C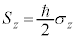 �Ƃ���悭�A
�Ƃ���悭�A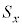 �C
�C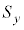 �C
�C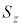 ���X�s���p�^���ʂ̕\���s��A
���X�s���p�^���ʂ̕\���s��A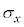 �C
�C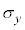 �C
�C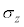 ���p�E���s���ƌ����܂��B�p�E���s��͎��̊W�������܂��B
���p�E���s���ƌ����܂��B�p�E���s��͎��̊W�������܂��B
����ɂ��ƁA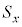 �C
�C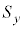 �C
�C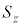 ���A
���A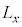 �C
�C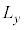 �C
�C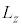 �Ɠ��l�̌����W�������܂��B
�Ɠ��l�̌����W�������܂��B
�f���q(����2)�ւÂ��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 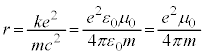
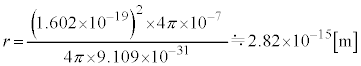
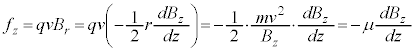 �@����B
�@����B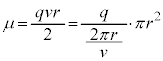
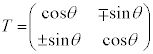 �@(��������)�@����C
�@(��������)�@����C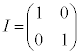 �Ƃ��āA�����s��́A
�Ƃ��āA�����s��́A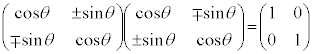
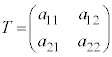 �̂Ƃ�
�̂Ƃ�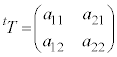 �C�s�����Q��)�Ƃ��������������܂��B�s��
�C�s�����Q��)�Ƃ��������������܂��B�s��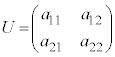 �̐����f���Ƃ���ꍇ�A
�̐����f���Ƃ���ꍇ�A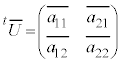 �ł����A
�ł����A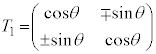 �C
�C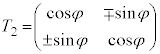 �ɂ��āA
�ɂ��āA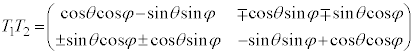
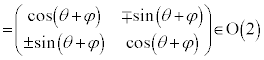 �@(��������)
�@(��������)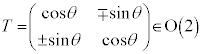 �ɑ���
�ɑ���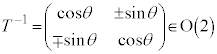 (��������)��
(��������)��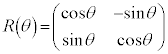 �Ƃ����^�C�v��
�Ƃ����^�C�v��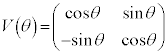 �Ƃ����^�C�v�ł��B
�Ƃ����^�C�v�ł��B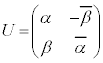 �Ə����܂��B
�Ə����܂��B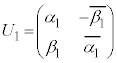 �C
�C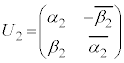 �C
�C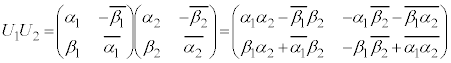
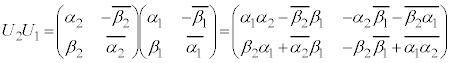
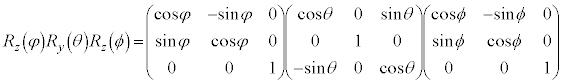
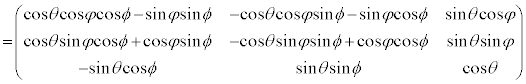
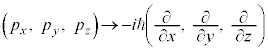
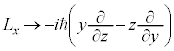 �C
�C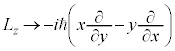
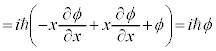
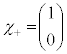 �C
�C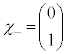
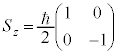 �Ƃ���悢���Ƃ�������܂��B
�Ƃ���悢���Ƃ�������܂��B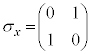 �C
�C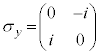 �C
�C �@����H
�@����H