�ʐϑ��x�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
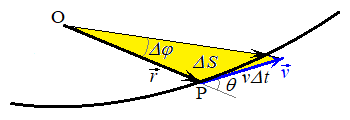 ���ʏ�Ō��_O�̂܂��ɉ^�����镨�̂��ʒuP�ɂ��āA���a�x�N�g��
���ʏ�Ō��_O�̂܂��ɉ^�����镨�̂��ʒuP�ɂ��āA���a�x�N�g��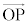 ����������
����������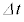 �̊Ԃɒʉ߂���ʐ�(�}�̉��F���F��)��
�̊Ԃɒʉ߂���ʐ�(�}�̉��F���F��)��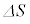 �ł���Ƃ��A
�ł���Ƃ��A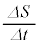 ���ʐϑ��x�Ƃ����B
���ʐϑ��x�Ƃ����B
�^���������F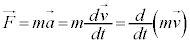 �̗��ӂ����a�x�N�g��
�̗��ӂ����a�x�N�g��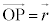 �Ƃ��O�����Ƃ�ƁA
�Ƃ��O�����Ƃ�ƁA
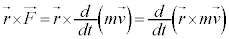 �@����@
�@����@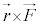 ����
����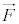 �����[�����g�ƌ����܂��B
�����[�����g�ƌ����܂��B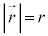 �C
�C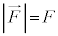 �C
�C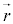 ��
��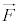 �̂Ȃ��p��θ�Ƃ��āA
�̂Ȃ��p��θ�Ƃ��āA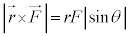 (
(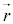 ��
��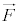 �Ƃō�镽�s�l�ӌ`�̖ʐ�)
�Ƃō�镽�s�l�ӌ`�̖ʐ�)
�E�ӂɏo�Ă���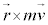 ���p�^�����ƌ����܂��B
���p�^�����ƌ����܂��B
�@�́A�p�^�����̎��ԕω������͂̃��[�����g�ɓ������A�ƌ����Ă��鎮�ł��B
�Ƃ���ŁA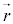 ��
��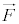 ����������������������̕����������Ƃ�(���̂Ƃ����������S���ƌ����܂�)�A
����������������������̕����������Ƃ�(���̂Ƃ����������S���ƌ����܂�)�A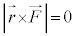 �ƂȂ�A�p�^�����̎��ԕω���0�ƂȂ�A�p�^���������ɂȂ�܂��B
�ƂȂ�A�p�^�����̎��ԕω���0�ƂȂ�A�p�^���������ɂȂ�܂��B
��L�̐}�ɂ����āA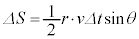 �ƂȂ�܂����A
�ƂȂ�܂����A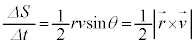 ���A�@��
���A�@��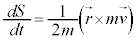 �Ƃ���A�p�^���������ł���A�ʐϑ��x�����ƂȂ�A���S�����ĉ^�����镨�̂��ʐϑ��x�͈��ł�(�P�v���[�̖@�����Q��)�B
�Ƃ���A�p�^���������ł���A�ʐϑ��x�����ƂȂ�A���S�����ĉ^�����镨�̂��ʐϑ��x�͈��ł�(�P�v���[�̖@�����Q��)�B
��L�̐}�ŁA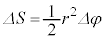 �Ƃ�������̂ŁA�ʐϑ��x��
�Ƃ�������̂ŁA�ʐϑ��x��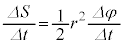 �̂悤�ɍl���邱�Ƃ��ł��܂��B
�̂悤�ɍl���邱�Ƃ��ł��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B