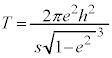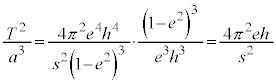�P�v���[�̖@���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���z�̂܂������f���̉^���ɂ��āA�ȉ������藧�B
�P�v���[�̑�1�@���F�f���͑��z���œ_�̈�Ƃ���ȉ~�O����`���ĉ^������B
�P�v���[�̑�2�@��(�ʐϑ��x�ۑ��̖@��)�F�f���Ƒ��z�����Ԑ������P�ʎ��Ԃ�����ɂɕ`���ʐ�(�ʐϑ��x)�͈��ł���B
�P�v���[�̑�3�@���F�f���̌��]������2��͑ȉ~�O���̒����a��3��ɔ�Ⴗ��B
17���I�����Ɋ����萯�p�t�P�v���[���A�t�e�B�R�E�u���[�G��������ꂽ�c��Ȋϑ����������20�N�������Ĕ��������@���B���̖@���̔����ɂ��A�R�y���j�N�X�̒n�����͗h�邬�Ȃ����̂ƂȂ�܂����B
�P�v���[�̖@���́A���z�̉�������f�������łȂ��A�n���̎��͂����l�H�q���Ȃǂɂ��Ă����藧���܂��B
���̖@���́A�j���[�g�������L�����̖@������ؖ�����Ă��܂��B
���z�̈ʒu�����_O�Ƃ���A���ʍ��W�A�ɍ��W���l���A�f��P���ʒu�x�N�g����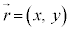 �Ƃ��܂��B
�Ƃ��܂��B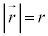 �C���aOP��x�����瑪������]�p��θ�Ƃ���ƁA
�C���aOP��x�����瑪������]�p��θ�Ƃ���ƁA
�f��P�����x�x�N�g��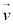 �́A
�́A
�f��P�������x�x�N�g��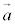 �́A
�́A
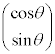 �͓��a
�͓��a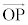 �̕����������x�N�g���A
�̕����������x�N�g���A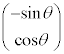 �͓��a
�͓��a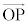 �Ɛ����ȕ����������x�N�g���ł��B
�Ɛ����ȕ����������x�N�g���ł��B
������A�f��P�������x�̓��a���������́A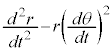 �C
�C
�f���Ƒ��z�̊Ԃɓ������L���������S��(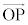 �ƕ��s�ȕ���������)�Ȃ̂ŁA�����x�̓��a�Ɛ����ȕ����̐�����0�ł��B
�ƕ��s�ȕ���������)�Ȃ̂ŁA�����x�̓��a�Ɛ����ȕ����̐�����0�ł��B
������A
�]���āA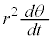 �͈��ɂȂ�܂��B���̈��l��
�͈��ɂȂ�܂��B���̈��l��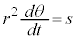 �@����A�@�Ƃ����܂��B
�@����A�@�Ƃ����܂��B
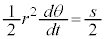 �́A�f��P���ʐϑ��x�Ȃ̂ŁA�f���̉^���ł́A�ʐϑ��x�����ɂȂ�A�P�v���[�̑�2�@�������藧���܂��B
�́A�f��P���ʐϑ��x�Ȃ̂ŁA�f���̉^���ł́A�ʐϑ��x�����ɂȂ�A�P�v���[�̑�2�@�������藧���܂��B
���z��������M�C�f����������m�C���L���͒萔��G�Ƃ��āA�f��P�́A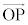 �Ƌt���������L����
�Ƌt���������L����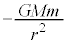 ���ĉ^�����܂����A���a�����ɂ����^���������́A
���ĉ^�����܂����A���a�����ɂ����^���������́A
����āA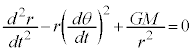 �@����B
�@����B
�f���̉^���̋O�Ղ��l���邽�߂ɁAr��θ�̊W�ׂ܂��Bt�Ɋւ��������θ�Ɋւ�������ɒ����܂��B�A��p���āA
�����ŁA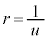 �Ƃ����ƁA
�Ƃ����ƁA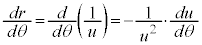
�܂��A�A��p���āA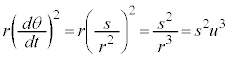 �C�������A�B�ɑ������ƁA
�C�������A�B�ɑ������ƁA
����́A�P�U���̌����F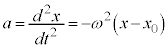 �Ɠ����`�����Ă��܂��B�P�U���̎��́A
�Ɠ����`�����Ă��܂��B�P�U���̎��́A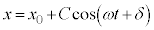 �̌`�ɂȂ�܂��B������A
�̌`�ɂȂ�܂��B������A
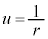 �Ȃ̂ŁA
�Ȃ̂ŁA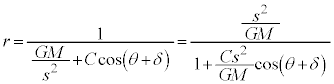
����́A���S���F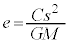 �ł���2���Ȑ��̕������ł��B
�ł���2���Ȑ��̕������ł��B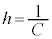 �Ƃ���ƁA
�Ƃ���ƁA
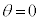 �̂Ƃ���r�ŏ��A�܂�f��P���ߓ��_�ɗ���Ƃ���A
�̂Ƃ���r�ŏ��A�܂�f��P���ߓ��_�ɗ���Ƃ���A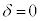
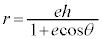 �@����B
�@����B
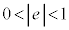 �ł���A�ȉ~
�ł���A�ȉ~
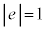 �ł���A������
�ł���A������
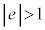 �ł���A�o�Ȑ�
�ł���A�o�Ȑ�
�ɂȂ�܂��B�f���̏ꍇ�ɂ́A���z�̉�������̂őȉ~�ɂȂ�܂��B���������P�v���[�̑�1�@���������܂����B
�B�ɂ����āA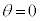 �̂Ƃ��ߓ��_�ŁA
�̂Ƃ��ߓ��_�ŁA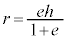 (
(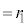 �Ƃ��܂�)
�Ƃ��܂�)
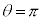 �̂Ƃ������_�ŁA
�̂Ƃ������_�ŁA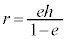 (
(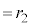 �Ƃ��܂�)
�Ƃ��܂�)
�ȉ~�����a��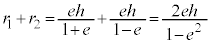 �C�����aa�͂���
�C�����aa�͂���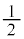 ��
��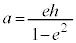
�ȉ~�̒��S�Əœ_�Ƃ�����c�́A
�Z���ab�́A����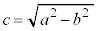 ���A
���A
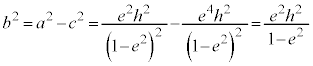 �@��
�@�� 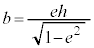
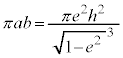 �C�f�������]����T�́A�ȉ~���ʐ����ʐϑ��x
�C�f�������]����T�́A�ȉ~���ʐ����ʐϑ��x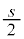 �Ŋ����āA
�Ŋ����āA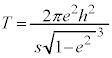
���]����T��2��������aa��3��Ŋ���ƁA
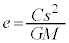 �C
�C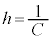 ���A
���A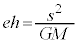
�� 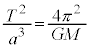
����ŁA�P�v���[�̑�3�@���������܂����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 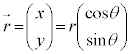
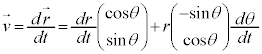
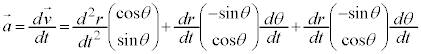
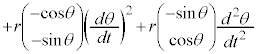
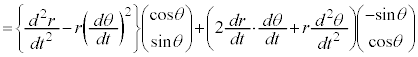
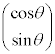 �͓��a
�͓��a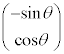 �͓��a
�͓��a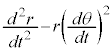 �C
�C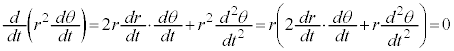
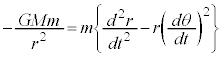
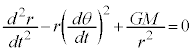 �@����B
�@����B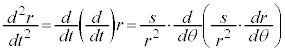
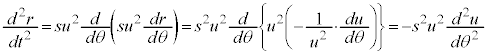
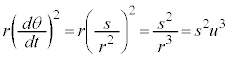 �C�������A�B�ɑ������ƁA
�C�������A�B�ɑ������ƁA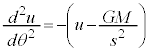
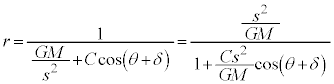
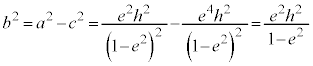 �@��
�@�� 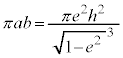 �C�f�������]����T�́A�ȉ~���ʐ����ʐϑ��x
�C�f�������]����T�́A�ȉ~���ʐ����ʐϑ��x