放物線 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
標準形：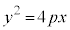
(
)
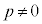放物線の定義：定点(焦点と言う)までの距離と、この定点を通らない定直線(準線と言う)までの距離とが等しい点の集合を放物線と言う。
放物線：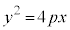
の焦点は
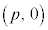，準線は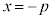
放物線の定義から放物線の方程式の標準形を導いてみます。
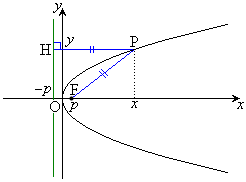右図で、焦点をF
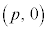，準線を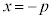
(
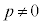)とし、放物線上の点P
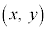と焦点までの距離
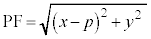と、準線までの距離
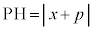を等しいとおくと、
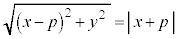
両辺を2乗して、
∴ 
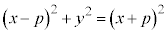
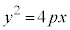
放物線：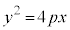
について、x軸、つまり、直線
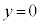を放物線の軸と言います。
放物線の方程式：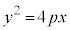
を満たす点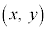
に対して、yのところに
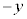を代入しても方程式が成り立ちます。従って、放物線はx軸、つまり、放物線の軸に関して対称です。
放物線の軸と放物線との交点、放物線：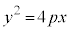
においては、原点O
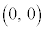を頂点と言います。
焦点がy軸上の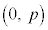
にあり、準線が
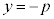となる場合は、同様にして、放物線の方程式は、
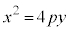となります。このときには、放物線の軸はy軸、つまり、直線
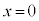，頂点はやはり原点Oです。
放物線：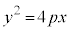
に接する傾きmの接線を求めてみます。
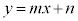と連立して、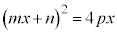
整理して、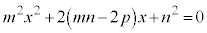
接するので、この2次方程式は重解を持ちます(2次方程式の一般論を参照)。
∴ 
∴ 
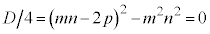
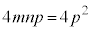
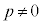より、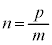
よって、求める傾きmの接線は、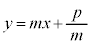
放物線：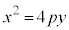
に接する傾きmの接線を求めてみます。
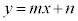と連立して、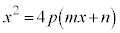
整理して、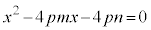
接するので、この2次方程式は重解を持ちます(2次方程式の一般論を参照)。
∴ 
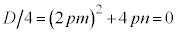
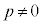より、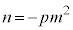
よって、求める傾きmの接線は、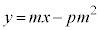
放物線の方程式：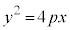
の両辺を陰関数の微分法で微分すると、
∴ 
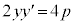
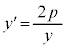
点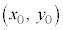
における接線の傾きは、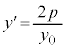
接点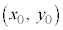
における接線は、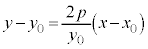
接点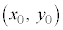
は放物線上の点なので、
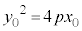より、
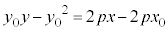
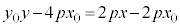
よって、接点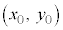
における接線は、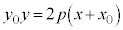
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。