量子力学の基礎
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
1924年ド・ブロイによって提唱された「物質波」の概念に基づき、シュレーディンガーによって構築された「量子力学」とはどんなものか、ニュートンの古典力学とどう違うのか、体験してみましょう。なお、ここでは、指数関数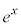 を、指数がややこしい形になることが多いので、
を、指数がややこしい形になることが多いので、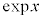 と書きます。
と書きます。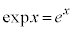 です。
です。
古典力学で、速度vで運動する粒子のエネルギーは、
です。速度を使わずに運動量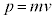 を用いて書くと、
を用いて書くと、
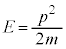 ・・・①
・・・①
1次元の波動は、波動方程式、
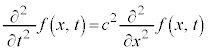 ・・・②
・・・②
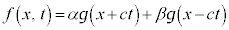 ・・・③
・・・③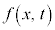 を②に代入してみると、
を②に代入してみると、
となるので②を満たし、③が②の解になっていることがわかります。
境界条件: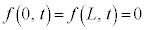
初期条件: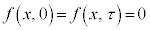
を課すと、例えば、
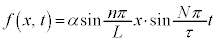 (n,Nは整数)
(n,Nは整数)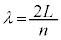 ,周期は
,周期は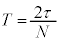 ,これを用いて、
,これを用いて、
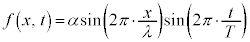 ・・・④
・・・④
これより、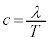 となっています(波の公式を参照)。ですが、ド・ブロイの公式より、
となっています(波の公式を参照)。ですが、ド・ブロイの公式より、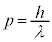 ,
,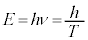 (h:プランクの定数,ν:振動数)
(h:プランクの定数,ν:振動数)
これを①: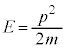 に代入すると、
に代入すると、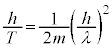 ,
,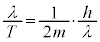 より、
より、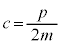 ということになり、粒子としての関係式①を満たせなくなってしまいます。
ということになり、粒子としての関係式①を満たせなくなってしまいます。
そこで、②を満たす解を、複素数を用いて記述し、
としてみます(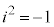 ,
,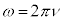 :角振動数,
:角振動数,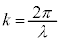 :波数)。
:波数)。
⑥を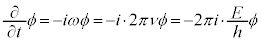 ,
,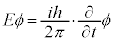
⑦を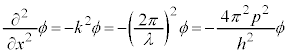 ,
,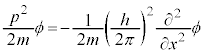
のように見ると、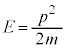 とするためには、
とするためには、
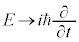 ,
,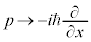 ・・・⑧ (
・・・⑧ (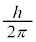 がよく出てくるので、
がよく出てくるので、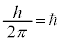 としています。
としています。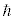 はディラック定数と呼ばれています)
はディラック定数と呼ばれています)
とすると、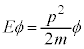 が満たされることになります。
が満たされることになります。
粒子の物質波が満たす波動関数ϕが従うべき方程式は、①で⑧の変換を施した、
ということになります。これを1次元のシュレーディンガー方程式と言います。複素数で波動関数ϕを扱い、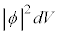 が微小体積
が微小体積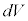 中に電子が存在する確率と考えます。
中に電子が存在する確率と考えます。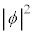 が確率密度関数です(正規分布を参照)。
が確率密度関数です(正規分布を参照)。
3次元の場合には、
となりますが、ラプラス演算子: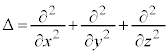 を用いて、
を用いて、
と書くことができます。⑧の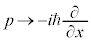 は、
は、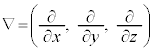 として、
として、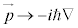 と書けます。運動エネルギー
と書けます。運動エネルギー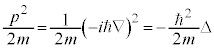 に加えて位置エネルギー
に加えて位置エネルギー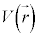 が存在する場合には、シュレーディンガー方程式は、
が存在する場合には、シュレーディンガー方程式は、
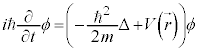 ・・・⑨
・・・⑨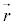 のみの関数
のみの関数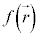 ,t のみの関数
,t のみの関数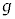 の積として、
の積として、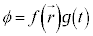 の形に書ける(変数分離と言います)として、⑨に代入すると、
の形に書ける(変数分離と言います)として、⑨に代入すると、
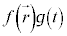 で両辺を割ると、
で両辺を割ると、
左辺はtのみの関数、右辺は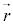 のみの関数です。これが等しくなるためには定数であることが必要です。この定数をEとおくと、偏微分
のみの関数です。これが等しくなるためには定数であることが必要です。この定数をEとおくと、偏微分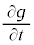 は通常の微分
は通常の微分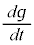 となり、
となり、
よって、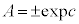 とおいて、
とおいて、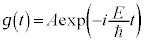
これより、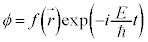
となりますが、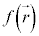 は、偏微分方程式:
は、偏微分方程式:
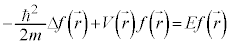 ・・・⑩
・・・⑩
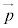 の代わりに
の代わりに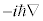 と書いたものを運動量演算子と言います。左辺の
と書いたものを運動量演算子と言います。左辺の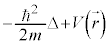 をハミルトニアン(エネルギー演算子)と言います。演算子Aを関数ϕに作用させ、
をハミルトニアン(エネルギー演算子)と言います。演算子Aを関数ϕに作用させ、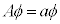 という微分方程式を解いて定数aが求められるとき、aを演算子Aの固有値と言います。また、その時の解ϕを固有値aに対する固有関数と言います。
という微分方程式を解いて定数aが求められるとき、aを演算子Aの固有値と言います。また、その時の解ϕを固有値aに対する固有関数と言います。
ここでは、時間を含まないシュレーディンガー方程式について考えます。
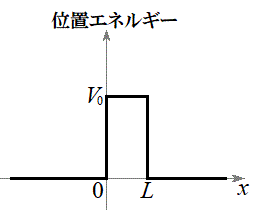 まず、一次元のシュレーディンガー方程式を考えます。右図のような高さ
まず、一次元のシュレーディンガー方程式を考えます。右図のような高さ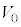 のポテンシャル障壁の問題を考えてみましょう。
のポテンシャル障壁の問題を考えてみましょう。
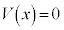 (
(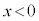 ),
), 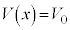 (
(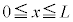 ),
), 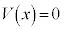 (
(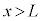 )
)
として、x軸負方向から粒子が入射する状況を考えます。
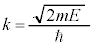 ,
,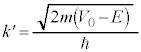 とおくと、シュレーディンガー方程式⑩は、
とおくと、シュレーディンガー方程式⑩は、
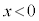 ,
,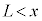 において、
において、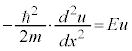 ,
,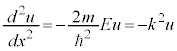 ・・・⑪
・・・⑪
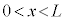 において、
において、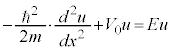 ,
,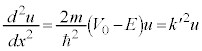 ・・・⑫
・・・⑫
となります。
 における⑪の解を、
における⑪の解を、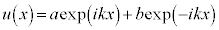 ・・・⑬
・・・⑬
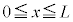 における⑫の解を、
における⑫の解を、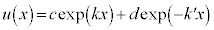 ・・・⑭
・・・⑭
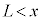 における⑪の解を、
における⑪の解を、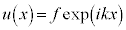 ・・・⑮
・・・⑮
とおきます。⑬の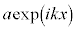 は電子の入射波、
は電子の入射波、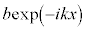 は電子の反射波、⑮の
は電子の反射波、⑮の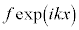 は透過波を意味しています。
は透過波を意味しています。
⑬を微分すると、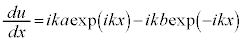
⑭を微分すると、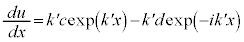
⑮を微分すると、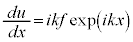
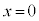 において、
において、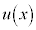 と
と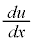 が連続なので、
が連続なので、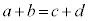 ,
,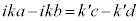
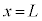 において、
において、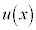 と
と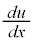 が連続なので、
が連続なので、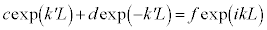 ,
,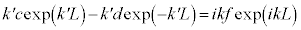
これらを解くと、
ここで、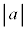 は
は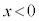 から進入してくる入射波の振幅、
から進入してくる入射波の振幅、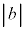 は反射波の振幅、
は反射波の振幅、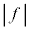 は透過波の振幅を表します。
は透過波の振幅を表します。
ポテンシャル障壁を粒子が透過する確率は、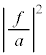 で表され、
で表され、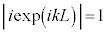 より、
より、
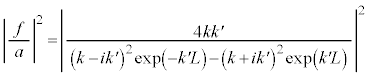
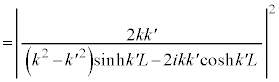
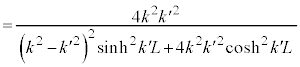
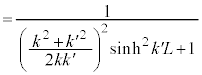
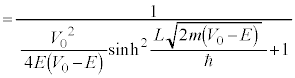 (
(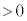 )
)
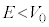 となる粒子でも、
となる粒子でも、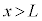 にも粒子の存在確率が出てくることがわかります。ポテンシャル障壁を越えるのに必要なエネルギーを持っていないのにもかかわらず、この障壁を越えてしまう粒子がある、という現象をトンネル効果と言いいます。
にも粒子の存在確率が出てくることがわかります。ポテンシャル障壁を越えるのに必要なエネルギーを持っていないのにもかかわらず、この障壁を越えてしまう粒子がある、という現象をトンネル効果と言いいます。
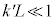 のときは、
のときは、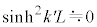 となり、透過率はほぼ1、つまり粒子はほぼ全数透過してしまいます。
となり、透過率はほぼ1、つまり粒子はほぼ全数透過してしまいます。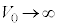 のとき、
のとき、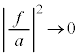 なので、障壁の高さが高いと粒子は障壁を越えられなくなります。
なので、障壁の高さが高いと粒子は障壁を越えられなくなります。
量子力学の基礎(その2)につづく。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 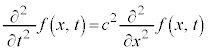 ・・・②
・・・②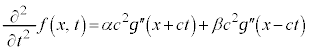
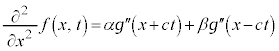
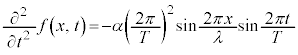
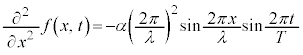
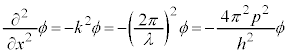 ,
,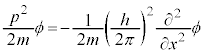
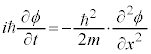
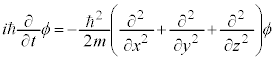
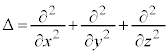 を用いて、
を用いて、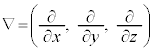 として、
として、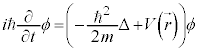 ・・・⑨
・・・⑨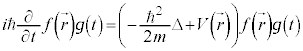
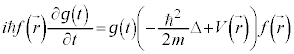
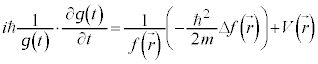
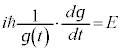
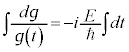
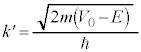 とおくと、シュレーディンガー方程式⑩は、
とおくと、シュレーディンガー方程式⑩は、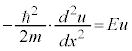 ,
,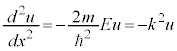 ・・・⑪
・・・⑪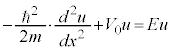 ,
,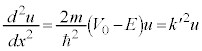 ・・・⑫
・・・⑫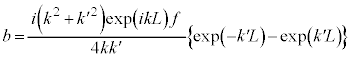
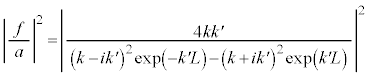
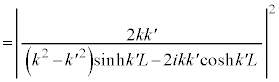
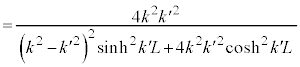
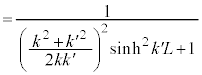
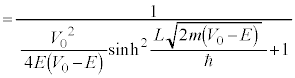 (
(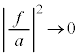 なので、障壁の高さが高いと粒子は障壁を越えられなくなります。
なので、障壁の高さが高いと粒子は障壁を越えられなくなります。