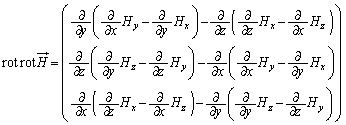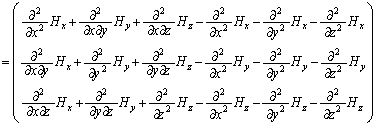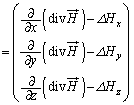�x�N�g����͂̌���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��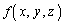 �ɂ��āA
�ɂ��āA
�x�N�g����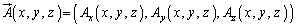 �ɂ��āA
�ɂ��āA
�܂��A
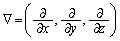 �Ƃ��āA
�Ƃ��āA
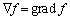 �C
�C �C
�C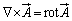 �@(�O�����Q��)
�@(�O�����Q��)
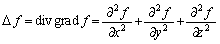 �@(Δ��Laplace���Z�q�ƌ���)
�@(Δ��Laplace���Z�q�ƌ���)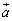 �C
�C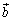 �C
�C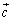 �ɂ��āA
�ɂ��āA
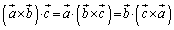 �@����@
�@����@
�K�E�X�̒藝�F�Ȗ�U�ň͂܂ꂽ�̈�V�ɂ��āA
���̑��̌���
�@�ɂ��āA
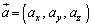 �C
�C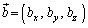 �C
�C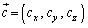 �Ƃ��܂��B
�Ƃ��܂��B
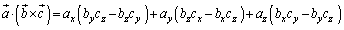 ��
�� 
 �������܂��B
�������܂��B
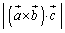 �C
�C �C
�C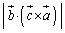 �́A��������A
�́A��������A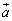 �C
�C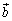 �C
�C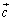 �ō���镽�s�Z�ʑ̂̑̐ς�\���Ă��܂�(�ǂ̖ʂ��ʂƌ��邩�̈Ⴂ�ł�)�B
�ō���镽�s�Z�ʑ̂̑̐ς�\���Ă��܂�(�ǂ̖ʂ��ʂƌ��邩�̈Ⴂ�ł�)�B
���w�ł́A�ϕ��Ɣ����̏��������ւ��ėǂ����A�ڍׂȋc�_���K�v�ł����A�����Ƃ��Ĉ������ł́A��O�I�ȏꍇ�������āA�ϕ��Ɣ����͌����ł���悤�Ȃ��̂�z�肵�܂��B�܂�A
�A�ɂ��āA
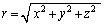 ���A
���A
���l�ɂ��āA
�B�ɂ��āA
�C�ɂ��āA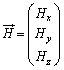 �Ƃ��āA
�Ƃ��āA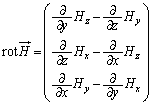 ���A
���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
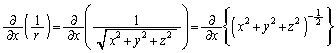
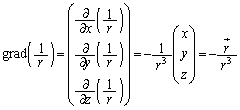
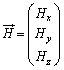 �Ƃ��āA
�Ƃ��āA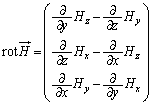 ���A
���A