�X�g�[�N�X�̒藝
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�X�g�[�N�X�̒藝�F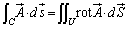
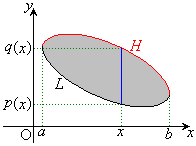
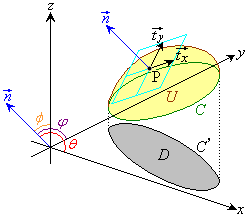 ��Ԓ��ɕȐ�C������(�ȒP�̂��߂ɓʂȋȐ����Ƃ��܂�)�AC�ň͂܂ꂽ�Ȗ�U������A�Ȗ�U��̓_P
��Ԓ��ɕȐ�C������(�ȒP�̂��߂ɓʂȋȐ����Ƃ��܂�)�AC�ň͂܂ꂽ�Ȗ�U������A�Ȗ�U��̓_P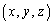 ���A
���A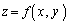 �����Ă���Ƃ��܂��Bx�Cy�Cz�̊��ł���x�N�g��
�����Ă���Ƃ��܂��Bx�Cy�Cz�̊��ł���x�N�g��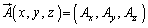 �ɂ��āA�Ȑ�C�ɉ�����
�ɂ��āA�Ȑ�C�ɉ�����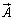 �����ϕ����邱�Ƃ��l���܂��B
�����ϕ����邱�Ƃ��l���܂��B
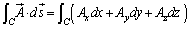 �@����@
�@����@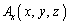 �ɂ��āA
�ɂ��āA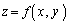 �������āA
�������āA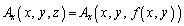 ��x�Cy�̊��ƍl���āA
��x�Cy�̊��ƍl���āA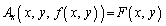 �Ƃ����܂��B
�Ƃ����܂��B
z��x�Cy�̊��Ȃ̂ŁA�A���藝��p����ƁA
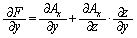 �@����A
�@����A
�Ȗ�U��̓_P�ɂ�����傫��1�̖@���x�N�g��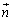 ��x���Cy���Cz���ƂȂ��p��θ�Cφ�Cϕ�Ƃ��āA
��x���Cy���Cz���ƂȂ��p��θ�Cφ�Cϕ�Ƃ��āA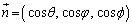 �ł����A�_P�ɂ�����Ȗ�U�̐ڕ��ʂ��A�_P��ʂ�xy���ʂɐ�������x���ɕ��s�ȕ��ʂŐ�ƁA����̒����̕����x�N�g����
�ł����A�_P�ɂ�����Ȗ�U�̐ڕ��ʂ��A�_P��ʂ�xy���ʂɐ�������x���ɕ��s�ȕ��ʂŐ�ƁA����̒����̕����x�N�g����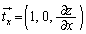 �C�ڕ��ʂ��A�_P��ʂ�xy���ʂɐ�������y���ɕ��s�ȕ��ʂŐ�ƁA����̒����̕����x�N�g����
�C�ڕ��ʂ��A�_P��ʂ�xy���ʂɐ�������y���ɕ��s�ȕ��ʂŐ�ƁA����̒����̕����x�N�g����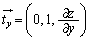 �C
�C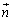 �́A����2�̃x�N�g������镽�ʂɐ����ȃx�N�g���Ȃ̂ŁA���҂��O�������߂�ƁA
�́A����2�̃x�N�g������镽�ʂɐ����ȃx�N�g���Ȃ̂ŁA���҂��O�������߂�ƁA
���̃x�N�g����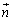 �ɕ��s�Ȃ̂ŁA
�ɕ��s�Ȃ̂ŁA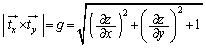 �Ƃ��āA
�Ƃ��āA
�Ə����܂��B
����āA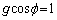 �C
�C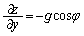 ���A�A���A
���A�A���A
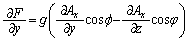 �@����B
�@����B
�Ȑ�C��xy���ʂւ̎ˉe�Ƃ��Ăł���Ȑ���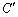 �C
�C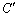 �ň͂܂��̈��D�Ƃ��܂��B
�ň͂܂��̈��D�Ƃ��܂��B
�Ȑ�C��̓_���Ȗ�U��̓_������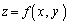 �����Ă��āA
�����Ă��āA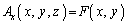 �ł���A
�ł���A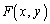 ��xy���ʏ��
��xy���ʏ��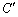 �ɂ�����x�Cy�̊��ƍl���āA
�ɂ�����x�Cy�̊��ƍl���āA
 �����ŁA
�����ŁA ��
�� �Ɉʒu���A
�Ɉʒu���A �ň͂܂��̈�D������x���W�̂Ƃ���Ő����Ƃ��ɁA
�ň͂܂��̈�D������x���W�̂Ƃ���Ő����Ƃ��ɁA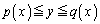 ���Ƃ��܂��B
���Ƃ��܂��B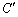 ��
��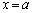 �C
�C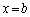 �ŏ㉺�ɕ����āA�㑤��H�C������L�Ƃ��āA
�ŏ㉺�ɕ����āA�㑤��H�C������L�Ƃ��āA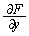 ��̈�D���ʐϕ�����ƁA
��̈�D���ʐϕ�����ƁA
����āA�B���A
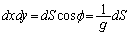 (�ʐϕ����Q��)���A�̈�D�ɂ�����ϕ����A�Ȗ�U�̐ϕ��Ƃ��āA
(�ʐϕ����Q��)���A�̈�D�ɂ�����ϕ����A�Ȗ�U�̐ϕ��Ƃ��āA
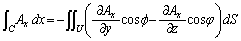 �@����C
�@����C
�C�Ɠ��l�ɂ��āA
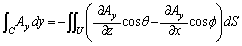 �@����D
�@����D
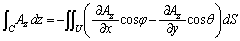 �@����E
�@����E
�傫����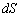 �C������
�C������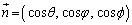 �ł���x�N�g��(�ʐϑf��)��
�ł���x�N�g��(�ʐϑf��)��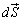 �Ƃ��āA
�Ƃ��āA
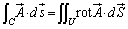 �@(rot�ɂ��Ă���]���Q��)
�@(rot�ɂ��Ă���]���Q��)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B