全微分
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
2変数x，yの関数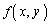
があって、x，yを両方動かしたときの変化分
について、
として、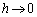
，
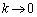のとき、
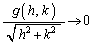となるのであれば、
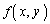は全微分可能である、と言います。
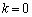のとき、
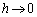として、
より、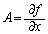
同様に、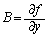
これより、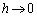
，
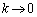のとき、
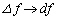として、
となりますが、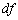
を全微分と言います。
全微分可能というのは、曲面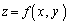
の接平面が存在することを意味します。
2変数関数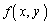
の変数x，yがさらにtの関数になっているとき、
が成り立ちます。
さらに、変数x，yが2変数u，vの関数になっているとき、
が成り立ちます(これを連鎖定理と呼びます)。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
