回転
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
コイルに電流を流すと、右ねじの法則に従って、コイルを貫く磁界が発生します。この現象を数学的に記述するために、回転と呼ばれる量を考えます。
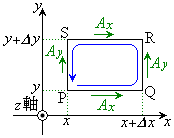 空間内で、右図のような、P
空間内で、右図のような、P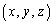 ,Q
,Q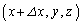 ,R
,R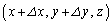 ,S
,S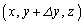 を4頂点とする微小な長方形に沿ってベクトル
を4頂点とする微小な長方形に沿ってベクトル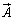 が一周して回る効果を考えます。
が一周して回る効果を考えます。
PQ上では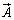 のx成分が
のx成分が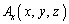 ,RS上では
,RS上では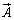 のx成分が
のx成分が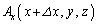 ,
,
QR上では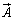 のy成分が
のy成分が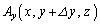 で、SP上では
で、SP上では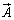 のy成分が
のy成分が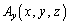 で、ここでは、ベクトルのx成分、y成分は、各辺上における値の変化を無視して、各辺上で一定値をとると考えることにします。
で、ここでは、ベクトルのx成分、y成分は、各辺上における値の変化を無視して、各辺上で一定値をとると考えることにします。
また、長方形をP→Q→R→S→Pと一周すると考えると、PQ上ではx軸の向き、QR上ではy軸の向きに進みますが、RS上ではx軸の向きと逆向きに、SP上ではy軸の向きと逆向きに進むので、ベクトル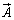 の寄与はそれぞれ、
の寄与はそれぞれ、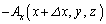 ,
,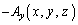 と考えられます。
と考えられます。
辺PQからの寄与と辺RSからの寄与を合わせると、yが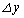 だけ変化したときの
だけ変化したときの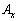 の変化率として、
の変化率として、
辺QRからの寄与と辺SPからの寄与を合わせると、xが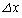 だけ変化したときの
だけ変化したときの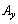 の変化率として、
の変化率として、
を考えることができます。
ここで、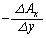 においては、z,xを固定して
においては、z,xを固定して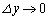 とし、
とし、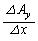 においては、y,zを固定して
においては、y,zを固定して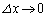 とすると、
とすると、
これより、微小な長方形に沿ってベクトル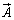 が一周して回る効果として、
が一周して回る効果として、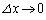 ,
,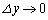 の極限で、
の極限で、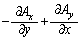 を考えることができます。
を考えることができます。
この長方形PQRSに沿って電流を流すときに、右ねじの法則によれば、長方形の中心(2本の対角線の交点)には、z軸方向の磁界ができます。そこで、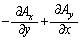 をz成分と考えます。
をz成分と考えます。
同様にして、x成分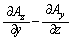 ,y成分
,y成分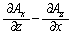 を考えることができます。
を考えることができます。
こうして得られたベクトルを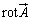 と書いて、ベクトル
と書いて、ベクトル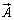 の回転(rotation)と言います。つまり、
の回転(rotation)と言います。つまり、
回転は、ベクトル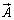 が各点において渦を巻く効果を表しています。
が各点において渦を巻く効果を表しています。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。