�K�E�X�̒藝
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�K�E�X�̒藝�F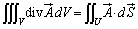
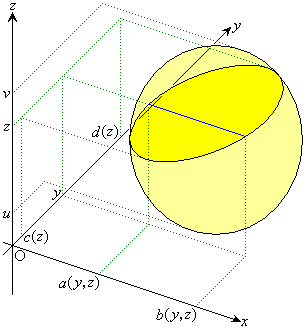 ��ԓ��̂���ʂȕȖ�U�ň͂܂ꂽ�̈�V�Œ�`����A�̈�V���̓_
��ԓ��̂���ʂȕȖ�U�ň͂܂ꂽ�̈�V�Œ�`����A�̈�V���̓_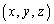 �ɂ�����l��
�ɂ�����l��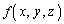 �ŗ^�������������Ƃ��܂��B
�ŗ^�������������Ƃ��܂��B
�̈�V�́A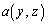 �C
�C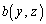 ��y�Cz�Ō��܂���C
��y�Cz�Ō��܂���C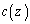 �C
�C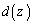 ��z�Ō��܂�����Ƃ��āA
��z�Ō��܂�����Ƃ��āA
�����ʂȗ̈悾�Ƃ��܂�(���Ƃ��낪����ꍇ�ɂ͂����ƕ��G�ł�)�B
��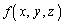 ��x���Δ���(y�Cz���Œ肵�Ĕ���)�������̂�̈�V�ɂ������̐ϕ����܂��B
��x���Δ���(y�Cz���Œ肵�Ĕ���)�������̂�̈�V�ɂ������̐ϕ����܂��B
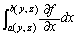 �́Ax���Œ肵�Đϕ�����̂ŁA
�́Ax���Œ肵�Đϕ�����̂ŁA
x���ɕ��s�Ȓ������Ȗ�U�Ɛڂ���_���Ȃ��łł���Ȑ��ŕȖʂ�x���W�̏���������A�Ƒ傫������B�ɕ����āA�ʐϕ����l����ƁA
�����ŁA�����y�Cz�ɑ���Ȗ�A�CB���ʐϑf����x���������̑��������Ă��܂��B�Ȗ�U�̋Ȗ�A���̕�����x���������̑��������Ă��܂��B2�̖ʐϕ���Ȗ�U�̖ʐϕ���ɂ܂Ƃ߂�ƁA
���l�Ȋ�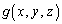 �C
�C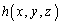 ���l���āA
���l���āA
�����ŁA�x�N�g���l���Ƃ��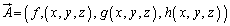 ���l����ƁA�Ȗ�U�̖ʐϑf�Ђ�
���l����ƁA�Ȗ�U�̖ʐϑf�Ђ�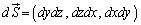 �Ƃ��āA
�Ƃ��āA
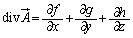 �C
�C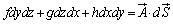 ���A
���A
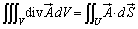 �@����@�@(div�ɂ��ẮA���U���Q��)
�@����@�@(div�ɂ��ẮA���U���Q��)
�@�����ӂ�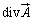 �́A�̈�V���̊e�_�Ńx�N�g��
�́A�̈�V���̊e�_�Ńx�N�g��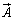 ���N���o������z�����܂ꂽ�肷��ʂ�\���Ă��܂��B�@���E�ӂ�
���N���o������z�����܂ꂽ�肷��ʂ�\���Ă��܂��B�@���E�ӂ�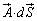 �́A�x�N�g��
�́A�x�N�g��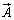 ���Ȗ�U�̊e�_����O�ɏo�čs���ʂ�\���Ă��܂��B
���Ȗ�U�̊e�_����O�ɏo�čs���ʂ�\���Ă��܂��B
�K�E�X�̒藝�́A�Ȗ�U�ň͂܂ꂽ�̈�V���̊e�_�ɂ����ăx�N�g��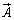 ���N���o������z�����܂ꂽ�肷��ʂ�S�����킹��ƁA�Ȗ�U��ʉ߂��ďo���肷��ʂɂȂ�A�Ƃ������Ƃ��Ӗ����Ă��܂��B
���N���o������z�����܂ꂽ�肷��ʂ�S�����킹��ƁA�Ȗ�U��ʉ߂��ďo���肷��ʂɂȂ�A�Ƃ������Ƃ��Ӗ����Ă��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B