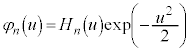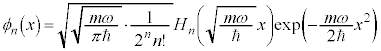量子力学の基礎からのつづきです。
質量m,角振動数ωのばね振り子のばね定数kを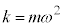 として位置エネルギーを
として位置エネルギーを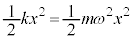 と考えたものを調和振動子といいます。
と考えたものを調和振動子といいます。
ここで、1次元の調和振動子の扱いが、古典論と量子論とでどう違うのかを考えます。
まず、古典論においては、力学的エネルギーが保存され一定値Eであるとして、
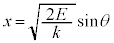 とおくと、
とおくと、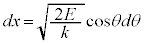
初期条件を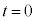 で
で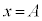 ,
,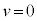 として、
として、
解は単振動ですが、Aは任意の正数をとり、エネルギーEのとる値は連続です。
量子論を用いて、結晶中で各原子が調和振動子として振動している状況を考えます。古典論の①で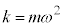 として、
として、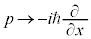 の置き換えを行う(量子力学の基礎を参照)と、シュレーディンガー方程式は、
の置き換えを行う(量子力学の基礎を参照)と、シュレーディンガー方程式は、
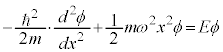 ・・・②
・・・②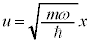 とおくと、
とおくと、
これを②に代入して、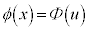 とすると、
とすると、
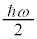 で割ると、
で割ると、
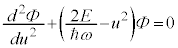 ・・・③
・・・③
ここで、③を解くための準備をします。
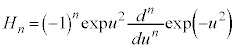 ・・・④
・・・④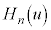 を考えます。最高次の係数が
を考えます。最高次の係数が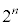 であるn次の多項式になります(後述の⑩式を用いて数学的帰納法で証明できます)。 ・・・(*)
であるn次の多項式になります(後述の⑩式を用いて数学的帰納法で証明できます)。 ・・・(*)
などとなっています。④で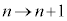 として、
として、
ここで、
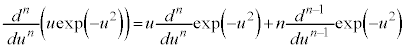 ・・・⑥
・・・⑥
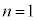 のとき、左辺は、
のとき、左辺は、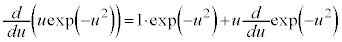
右辺は、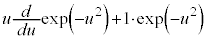
よって、左辺=右辺で、成り立ちます。
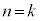 のとき、⑥が成り立つとして、
のとき、⑥が成り立つとして、
の両辺をuで微分して、
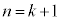 のときにも⑥が成立します。よって、すべての自然数nで⑥が成立します。
のときにも⑥が成立します。よって、すべての自然数nで⑥が成立します。
⑥を⑤に代入して、
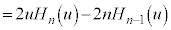 ・・・⑦
・・・⑦
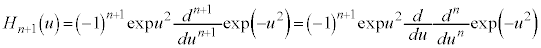 ・・・⑧
・・・⑧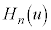 の定義④:
の定義④: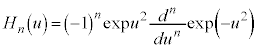 より、
より、
⑧に代入して、
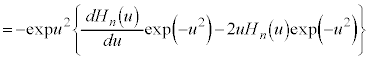
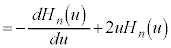 ・・・⑨
・・・⑨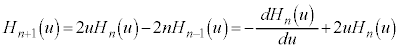
∴ 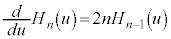 ・・・⑩
・・・⑩ ⑨を微分して、
⑩より、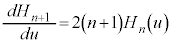
∴ 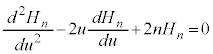 ・・・⑪
・・・⑪ これが、エルミート多項式が満たすべき微分方程式です。
ところで、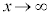 ,つまり、
,つまり、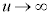 のとき、
のとき、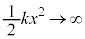 でポテンシャル障壁が高くなるので、電子は無限の彼方には行きません。つまり、③において、
でポテンシャル障壁が高くなるので、電子は無限の彼方には行きません。つまり、③において、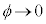 ,
,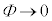
そこで、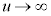 のとき、
のとき、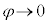 となるような関数として、
となるような関数として、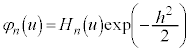 を考えます。これより、
を考えます。これより、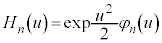 とおいて
とおいて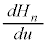 ,
,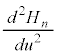 を調べると、、
を調べると、、
⑪に代入して、
これより、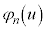 について、
について、
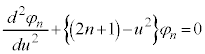 ・・・⑫
・・・⑫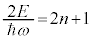 ,つまり、
,つまり、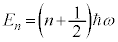 (
(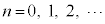 )であれば、
)であれば、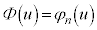 となることがわかります。
となることがわかります。
これより、エネルギーEはとびとびの値を取ります。各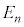 が固有値です。プランクの量子仮説は、シュレーディンガーの理論の結果を先取りしたものになっています。
が固有値です。プランクの量子仮説は、シュレーディンガーの理論の結果を先取りしたものになっています。
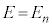 に対応する固有関数は、
に対応する固有関数は、
となります。元のシュレーディンガー方程式②の解は、
です。ここで、異なる固有値に対する固有関数同士の積の積分を調べます。
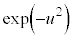 は何回微分しても、(uの多項式)×
は何回微分しても、(uの多項式)×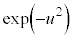 の形になるので、
の形になるので、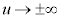 のとき上式中括弧内第1項は0に近づきます。よって、
のとき上式中括弧内第1項は0に近づきます。よって、
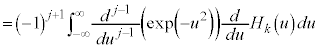 ・・・⑬
・・・⑬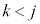 のときには、(*)に書いたように、
のときには、(*)に書いたように、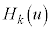 はk次の多項式なので
はk次の多項式なので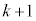 回微分した時点でゼロになり、
回微分した時点でゼロになり、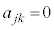 となります。またjとkを入れ替えて考えると、
となります。またjとkを入れ替えて考えると、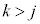 のときも
のときも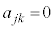 です。つまり、
です。つまり、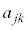 を成分とする行列の非対角成分はゼロです。対角成分は、
を成分とする行列の非対角成分はゼロです。対角成分は、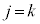 のとき
のとき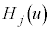 は最高次の係数が
は最高次の係数が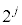 であるj次の多項式で、部分積分を
であるj次の多項式で、部分積分を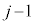 回行った後、
回行った後、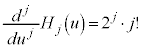 (
(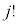 は
は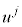 をj回微分するところから出てきます)となるので、⑬で
をj回微分するところから出てきます)となるので、⑬で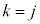 としてさらに
としてさらに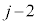 回部分積分を続けると、
回部分積分を続けると、
よって、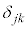 を、
を、 (
(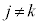 のとき),
のとき),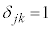 (
(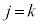 のとき)として定義(クロネッカーのδと言います。
のとき)として定義(クロネッカーのδと言います。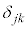 を要素とする行列は単位行列です)すると、
を要素とする行列は単位行列です)すると、
この関係を固有関数の直交性と言います。全確率: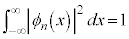 を満たす、②の規格化された解は、
を満たす、②の規格化された解は、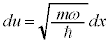 より、
より、
となります。
量子力学の基礎(その3)につづく。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 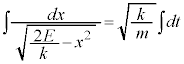
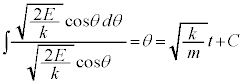 (C:積分定数)
(C:積分定数)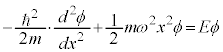 ・・・②
・・・②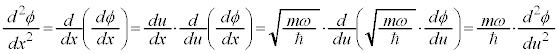
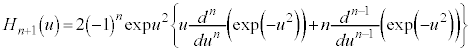
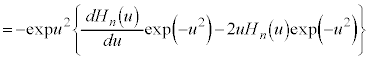
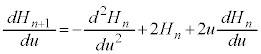
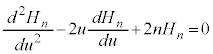 ・・・⑪
・・・⑪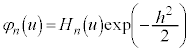 を考えます。これより、
を考えます。これより、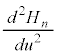 を調べると、、
を調べると、、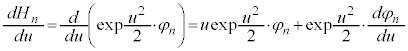
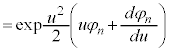
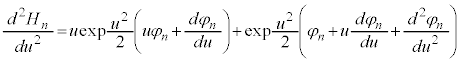
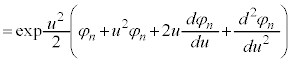
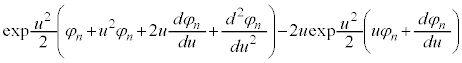
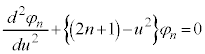 ・・・⑫
・・・⑫