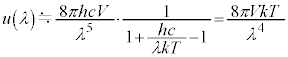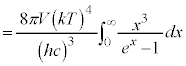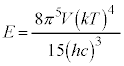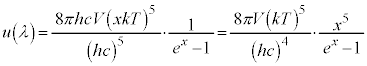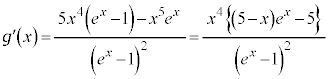�����t��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
1860�N��A�u����̑���͌��_�⑽�����ɂ���Ăł͂Ȃ��A�S�ƌ��ɂ���Ă̂݉��������v�Ƃ����������s�����S���ɑ��r�X�}���N�̉��ŁA�����̃v���V���́A�h�C�c�����}��ׂ��d�H�Ɛ��i�̌R������������Ƃ�A�����S�|�����邽�߂̋Z�p�J����簐i���Ă��܂����B���̂��߂ɂ́A�n�z�F���̉��x��n�z�F���̌��̐F�Ŕ��f���Ă����E�l�́u�ځv�𗝘_�I�ɉ𖾂��A�n�z�F�̒��ŗn�Z�����S�z�������̐F�𐧌䂷��ׂ��A�h�C�c�ł͍����t�˂̌������傫���i�����܂����B
���̂Ƃ����̂́A�����z�����邾���ŕ��˂��邱�Ƃ̂Ȃ��������̂̂��Ƃ��w���܂��B�X�X�Ő^�����ɂȂ����n�z�F�������܂��ɂ���ɑ������܂��B�����I�ɂ́A������x���荞�ނƏo�Ă���Ȃ������ȓ���������Ƃ��ă��f��������܂��B
1879�N�A�I�[�X�g���A�̃V���e�t�@���́A���̂̔M���˂��S�G�l���M�[����Ή��x��4��ɔ�Ⴗ�邱�Ƃ����A1884�N�ɁA��q�̃{���c�}���ƂƂ��ɁA�M�͊w��p���āA�V���e�t�@���E�{���c�}���̖@���Ƃ��ė��_�I�ɐ������܂����B
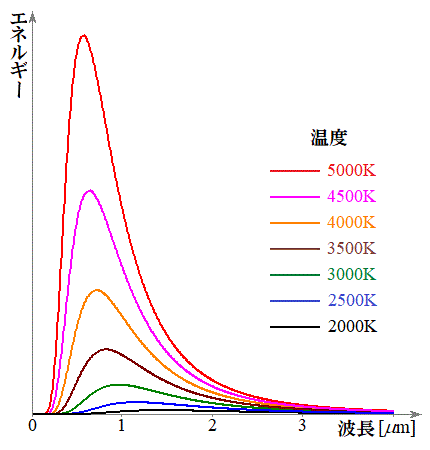 �����t�˂��G�l���M�[�́A���̂����x�Ƃ���������o�������̐F(�����g��)�Ƃ̊ԂɉE�}�̂悤�ȊW������܂��B���x�����܂荂���Ȃ������͐Ԃ��F�̌�����o���܂����A���x�������Ȃ�ɏ]�����G�l���M�[���ő�ɂȂ��g�����Z���Ȃ�A��F�A���F�A����������ɂȂ��Ă��܂��B
�����t�˂��G�l���M�[�́A���̂����x�Ƃ���������o�������̐F(�����g��)�Ƃ̊ԂɉE�}�̂悤�ȊW������܂��B���x�����܂荂���Ȃ������͐Ԃ��F�̌�����o���܂����A���x�������Ȃ�ɏ]�����G�l���M�[���ő�ɂȂ��g�����Z���Ȃ�A��F�A���F�A����������ɂȂ��Ă��܂��B
�C�M���X�̃��C���[�́A1889�N�A���̂̃��f���ƂȂ��Ă�����ŁA�}�N�X�E�F���̓d���������������g�ƂȂ��Ă���d���g�̔g�������߂܂����B���g���g���͋C���̐U���Ɠ��l�ɂƂтƂт̒l���Ƃ�܂����A�g����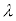 ��
��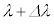 �̊Ԃɂ���g���̏�Ԃ̊e�X���G�l���M�[�����z�������G�l���M�[
�̊Ԃɂ���g���̏�Ԃ̊e�X���G�l���M�[�����z�������G�l���M�[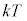 (k�F�{���c�}���萔�AT�F��Ή��x)�����Ƃ��ăX�y�N�g�����z��\���������߂܂����B���̌��ʂ́A����ȍ~���A���C���[���g�A�܂��W�[���Y�ɂ��C�����Ȃ���āA�P�ʑ̐ϓ�����A
(k�F�{���c�}���萔�AT�F��Ή��x)�����Ƃ��ăX�y�N�g�����z��\���������߂܂����B���̌��ʂ́A����ȍ~���A���C���[���g�A�܂��W�[���Y�ɂ��C�����Ȃ���āA�P�ʑ̐ϓ�����A
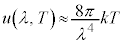 �@����@
�@����@
�h�C�c�̃E�B�[����1893�N�A�{���c�}���̎�@�������t�˂ɉ��p���A�G�l���M�[�ő�ƂȂ��g�������x�ɔ���Ⴗ�邱�Ƃ��܂����B������E�B�[���̕ψʑ��ƌ����܂��B
����ɃE�B�[���́A1896�N�A���̔g��λ���d���g���G�l���M�[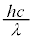 (h�Cc�͒萔)�����ÓT�͊w�̗��q�Ƃ������z�C���̂悤�ɐU��܂��Ƃ��āA�C�̕��q�^���_�Ɠ��l�̍l�@����A�P�ʑ̐ϓ�����A�d���g���G�l���M�[���z��^���鎮�A
(h�Cc�͒萔)�����ÓT�͊w�̗��q�Ƃ������z�C���̂悤�ɐU��܂��Ƃ��āA�C�̕��q�^���_�Ɠ��l�̍l�@����A�P�ʑ̐ϓ�����A�d���g���G�l���M�[���z��^���鎮�A
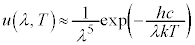 �@����A
�@����A
�h�C�c�̃v�����N�́A�E�B�[���̗��_���l�@���钆�ŁA���ł͓d���g���Œ�[�����̐U���Ɠ��l�ɒ��g������Ă���A���g���G�l���M�[���A�ŏ��P��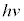 �̐����{�A�Ƃ����A�ƂтƂт̒l���G�l���M�[�����A�Ƃ��������u���܂����Bν�͓d���g���U�����Ah�͒萔�ŁA�v�����N�萔�ƌĂ�A���݂ł́A
�̐����{�A�Ƃ����A�ƂтƂт̒l���G�l���M�[�����A�Ƃ��������u���܂����Bν�͓d���g���U�����Ah�͒萔�ŁA�v�����N�萔�ƌĂ�A���݂ł́A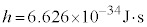 �Ƌ��߂��Ă��܂��B���g�Ƃ����A�C�f�A�̓��C���[�Ɠ����A�G�l���M�[�ɍŏ��P�ʂ�����A�Ƃ����A�C�f�A�́A�A�ɐ��ɍŏ��P�ʁu�d�q�v������ƍl�����X�g�[�j�[�Ɠ���(�d�q���Q��)�ł��B
�Ƌ��߂��Ă��܂��B���g�Ƃ����A�C�f�A�̓��C���[�Ɠ����A�G�l���M�[�ɍŏ��P�ʂ�����A�Ƃ����A�C�f�A�́A�A�ɐ��ɍŏ��P�ʁu�d�q�v������ƍl�����X�g�[�j�[�Ɠ���(�d�q���Q��)�ł��B
����ɁA�v�����N�͂����̒��g�����xT�̔M���ɐڂ��Ă��ĔM���t�ɂ���Ƃ��āA�n���{���c�}�����z�ɏ]�������W�c(���v�͊w�̊�b���Q��)�ƍl���A���g���G�l���M�[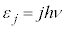 (
(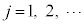 )�������m����
)�������m����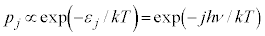 (k�F�{���c�}���萔)�ŗ^������Ɖ��肵�܂����B
(k�F�{���c�}���萔)�ŗ^������Ɖ��肵�܂����B
���A
�Ƃ���ΑS�m����1�ɂȂ�܂��B�G�l���M�[�̕��ϒl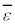 �́A
�́A
�ŗ^�����܂��B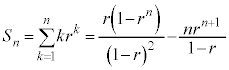 ���An���[���ɑ傫���A
���An���[���ɑ傫���A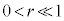 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A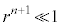 �C
�C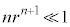 ���A
���A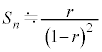 �C������g���ƁA
�C������g���ƁA
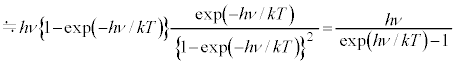 �@����B
�@����B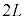 �ł��B�d���g���`�d���x������c�Ȃ̂ŁA�ŗL�U�����U������
�ł��B�d���g���`�d���x������c�Ȃ̂ŁA�ŗL�U�����U������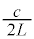 �C�d���g���U����ν�͂���n�{���\�Ȃ̂ŁA
�C�d���g���U����ν�͂���n�{���\�Ȃ̂ŁA
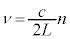 �@����C
�@����C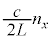 �C
�C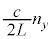 �C
�C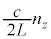 �Ƃ���ƁA
�Ƃ���ƁA
�Ƃ���ŁA���an�̋������a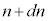 �̋��̊Ԃ̋��k�ɂ���i�q�_
�̋��̊Ԃ̋��k�ɂ���i�q�_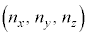 �̐��́A���an�̋��̕\�ʐ�
�̐��́A���an�̋��̕\�ʐ�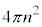 �ɋ��k�̌���
�ɋ��k�̌���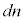 �����������k�̑̐�
�����������k�̑̐�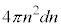 �ŗ^�����A���̂����A
�ŗ^�����A���̂����A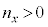 �C
�C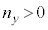 �C
�C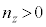 �������̂͂���
�������̂͂���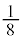 �ŁA
�ŁA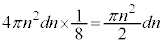 ��������܂��B�C��p���āA
��������܂��B�C��p���āA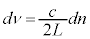 ���A�d���g�̐U���̌��́A
���A�d���g�̐U���̌��́A
����ɁA�Ό��̎��R�x���d���g�̐i�s�����ɑ��Đ�����2��������̂ŁA�G�l���M�[�̕��ϒl���B�ƂȂ�d���g�̏�Ԑ��́A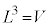 (�̑̐�)�Ƃ��āA
(�̑̐�)�Ƃ��āA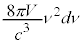 ���������āA�U����ν�ɑ����G�l���M�[�́A
���������āA�U����ν�ɑ����G�l���M�[�́A
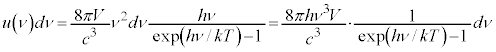 �@����D
�@����D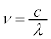 ���A�d���g���G�l���M�[���g���Ƃ̊W�́A
���A�d���g���G�l���M�[���g���Ƃ̊W�́A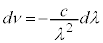 ���A
���A
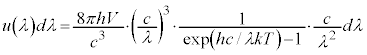 �@(�}�C�i�X���Ȃ��Ă��܂�)
�@(�}�C�i�X���Ȃ��Ă��܂�)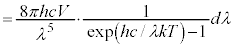 �@����E
�@����E
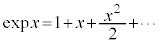 (�}�N���[�����W�J���Q��)���A�g��λ���傫��
(�}�N���[�����W�J���Q��)���A�g��λ���傫��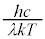 ���������Ƃ��A�E�́A
���������Ƃ��A�E�́A
���A
����̓��C���[�ƃW�[���Y�������@�ł��B
����A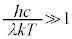 �̂Ƃ��A�܂�A���x���Ⴂ���g�����������Ƃ��A�E�̕����1�������ł��āA
�̂Ƃ��A�܂�A���x���Ⴂ���g�����������Ƃ��A�E�̕����1�������ł��āA
����̓E�B�[�����t�ˎ��A�ł��B
�S�G�l���M�[�́A�D��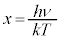 �Ƃ����Ēu���ϕ�����ƁA
�Ƃ����Ēu���ϕ�����ƁA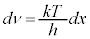 ���A
���A
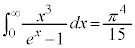 (�v�Z�͏ȗ�)�ƂȂ�̂ŁA�S�G�l���M�[�����U���邱�Ƃ͂Ȃ��A
(�v�Z�͏ȗ�)�ƂȂ�̂ŁA�S�G�l���M�[�����U���邱�Ƃ͂Ȃ��A
�S�G�l���M�[��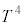 �ɔ�Ⴕ�A����̓V���e�t�@���E�{���c�}���̖@���ł��B
�ɔ�Ⴕ�A����̓V���e�t�@���E�{���c�}���̖@���ł��B
�E��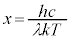 �Ƃ����ƁA
�Ƃ����ƁA
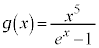 �Ƃ����ƁA
�Ƃ����ƁA
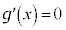 �Ƃ���ƁA
�Ƃ���ƁA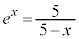 �@����F
�@����F
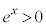 �Ȃ̂�
�Ȃ̂�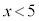 �ł����A
�ł����A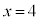 �̂Ƃ�
�̂Ƃ�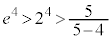 �ł����A
�ł����A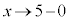 �̂Ƃ��A
�̂Ƃ��A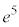 �͗L���Ȑ��ł����A
�͗L���Ȑ��ł����A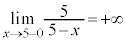 �Ȃ̂ŁA�F��
�Ȃ̂ŁA�F��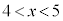 �͈̔͂ɉ��������܂��B���̉���α(�ق�
�͈̔͂ɉ��������܂��B���̉���α(�ق�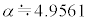 �ł�)�Ƃ����ƁA
�ł�)�Ƃ����ƁA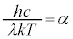 �C�����A�e���x�ɑ��āA��}���G�l���M�[���ő�Ƃ����g����
�C�����A�e���x�ɑ��āA��}���G�l���M�[���ő�Ƃ����g����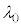 �Ƃ���ƁA
�Ƃ���ƁA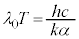 (= ���)�ƂȂ�܂����A����̓E�B�[���̕ψʑ��ł��B
(= ���)�ƂȂ�܂����A����̓E�B�[���̕ψʑ��ł��B
�������A�v�����N���t�ˎ��́A�S�g���ɓn���Ď����l�Ƃ悭�����Ă��܂����B�������āA1900�N�A�v�����N�́A��(�d���g)���G�l���M�[�͘A���I�Ȓl�����̂ł͂Ȃ��A�ŏ��P��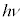 �̐����{�̒l�̂ݎ��A�Ƃ������_(�v�����N�̗ʎq�����ƌ����܂�)�Ɏ���܂����B���ꂪ���Ӗ��ɂ��ẮA�A�C���V���^�C�������d�����̐���(1905�N)���ő̔�M�̗��_(1907�N)��҂��ƂɂȂ�܂��B
�̐����{�̒l�̂ݎ��A�Ƃ������_(�v�����N�̗ʎq�����ƌ����܂�)�Ɏ���܂����B���ꂪ���Ӗ��ɂ��ẮA�A�C���V���^�C�������d�����̐���(1905�N)���ő̔�M�̗��_(1907�N)��҂��ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 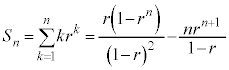 ���An���[���ɑ傫���A
���An���[���ɑ傫���A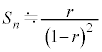 �C������g���ƁA
�C������g���ƁA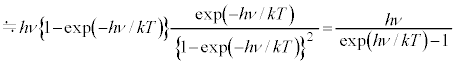 �@����B
�@����B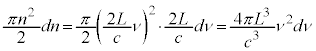
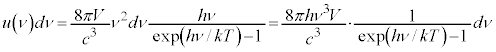 �@����D
�@����D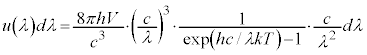 �@(�}�C�i�X���Ȃ��Ă��܂�)
�@(�}�C�i�X���Ȃ��Ă��܂�)