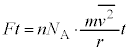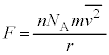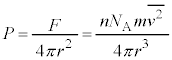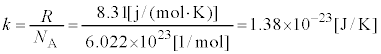�C�̕��q�^���_�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
����m�̋C�̕��q�����x��2��̕��ϒl��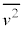 �Ƃ��āA�C�̕��q1���G�l���M�[�̕��ϒlε�́A�C�̂���Ή��x��T�C�{���c�}���萔��
�Ƃ��āA�C�̕��q1���G�l���M�[�̕��ϒlε�́A�C�̂���Ή��x��T�C�{���c�}���萔�� �Ƃ��āA
�Ƃ��āA
�P���q���q���z�C���ł́A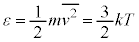
2���q���q���z�C���ł́A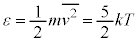
�{���c�}���萔k�ƁA�A�{�K�h����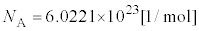 �C�C�̒萔
�C�C�̒萔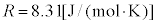 �̊Ԃɂ́A
�̊Ԃɂ́A
�Ƃ����W������(�A�{�K�h�����A�C�̒萔�ɂ��ẮA���z�C�����Q��)�B
��σ�����M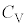 �́A
�́A
�P���q���q���z�C���ł́A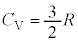
2���q���q���f�C���ł́A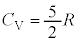
���z�C�̂������G�l���M�[U�́A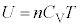
�P���q���q���z�C���ł́A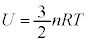
2���q���q���z�C���ł́A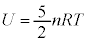
����@�C�̂̐U�镑�����C�̕��q1�̉^���ɒ��ڂ��čl���܂��B������C�̕��q�^���_�ƌ����܂��B
�C�̕��q1�̉^���ɒ��ڂ��A�C�̕��q1�̑��x��G�l���M�[���l���闧����e�����I����'�ƌ����܂��B����ɑ��āA�C�̑��̂ɒ��ڂ��A�C�̂̈��́A�̐ρA���x���l���闧����e�����I����'�ƌ����܂��B
�e��̌`��ɂ���ďꍇ�������A�����̗e���̏ꍇ�A���`�e���̏ꍇ���l���܂��B
�e�ꍇ�ɂ����āA�e�����n[mol]�̋C�̂���������Ă���Ƃ��܂��B�A�{�K�h������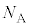 �Ƃ��āA�e����ɂ�
�Ƃ��āA�e����ɂ�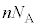 �̋C�̕��q�����݂��܂��B
�̋C�̕��q�����݂��܂��B
�C�̕��q1������m�̏����Ƃ��A�C�̕��q�̑傫���ƋC�̕��q���݊Ԃɓ����͂����܂��B�܂�A���z�C�����Ƃ��čl���܂��B
�܂��A�e��̓��ǂƋC�̕��q�́A���S�e���Փ˂�����Ƃ��čl���܂��B
(1) �����̗e���̏ꍇ
���L�̗����̗e����ɋC�̂���������Ă���Ƃ��܂��B
�����̂�1�̒��_����o��3�ӂɉ����āAx���Ay���Az�����Ƃ�A�C�̕��q1�����x��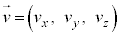 �Ƃ��܂��B
�Ƃ��܂��B
�C�̕��q�ɓ����d�͂͏�������������ƁA�C�̕��q��x�������Cy�������Cz����������ʂł��Ȃ��̂ŁA�e����̋C�̕��q�S�̂̕��ς��Ƃ�ƁA�e���������x������2�敽�ϒl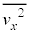 �C
�C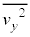 �C
�C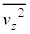 �͓������ƍl���邱�Ƃ��ł��܂�(���x�������̂̕��ς͊e�����Ƃ�0)�B�܂�A
�͓������ƍl���邱�Ƃ��ł��܂�(���x�������̂̕��ς͊e�����Ƃ�0)�B�܂�A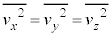
�]���āA�C�̕��q�̑��x��2�敽�ϒl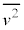 �ɂ��āA
�ɂ��āA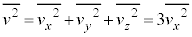
�� 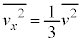 �@����@
�@����@
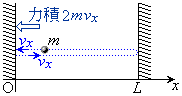 ���A�C�̕��q1���Ayz���ʂ����x
���A�C�̕��q1���Ayz���ʂ����x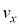 �Ŋ��S�e���Փ˂���Ƃ��܂��B�Փˌ�����x��
�Ŋ��S�e���Փ˂���Ƃ��܂��B�Փˌ�����x��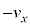 �ƂȂ�A���̋C�̕��q�̏ՓˑO��ł��^���ʂ̕ω��́A
�ƂȂ�A���̋C�̕��q�̏ՓˑO��ł��^���ʂ̕ω��́A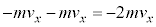 yz���ʂ����̋C�̕��q1������͐��́A�����^���ʂ̕ω��̔���p�ŁA
yz���ʂ����̋C�̕��q1������͐��́A�����^���ʂ̕ω��̔���p�ŁA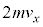
���̋C�̕��q�́Ayz���ʂɏՓ˂�����A����������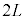 �C���x
�C���x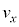 �ʼn^������̂ŁA�����ɗv����������
�ʼn^������̂ŁA�����ɗv����������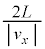 �Ct�b�Ԃɂ�
�Ct�b�Ԃɂ�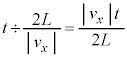 ��Ayz���ʂƏՓ˂��܂��B
��Ayz���ʂƏՓ˂��܂��B
�]���āAt�b�Ԃ�yz���ʂ����̋C�̕��q1������͐��̑傫���́A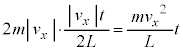 yz���ʂ��S�C�̕��q����t�b�ԂɎ��͐��̑傫���́A����
yz���ʂ��S�C�̕��q����t�b�ԂɎ��͐��̑傫���́A����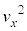 ��S�C�̕��q�ł̕��ϒl
��S�C�̕��q�ł̕��ϒl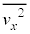 �ɒu�������āA�C�̕��q�̌�
�ɒu�������āA�C�̕��q�̌�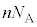 �����������̂ɂȂ�A
�����������̂ɂȂ�A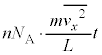 �ł��Byz���ʂ��S�C�̕��q��������̑傫����F�Ƃ���t�b�ԂɎ��͐��̑傫���́A
�ł��Byz���ʂ��S�C�̕��q��������̑傫����F�Ƃ���t�b�ԂɎ��͐��̑傫���́A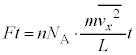
�� 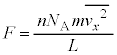 �@���A
�@���A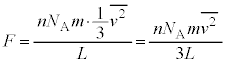 yz���ʁA�]���āA�����̂̑��̖ʑS�Ăɂ��āA�e�ʂ�������P�́A���̑傫��F��ʐ�
yz���ʁA�]���āA�����̂̑��̖ʑS�Ăɂ��āA�e�ʂ�������P�́A���̑傫��F��ʐ�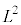 �Ŋ����āA
�Ŋ����āA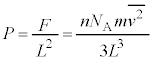
�����̗e����̐�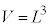 ��p���āA
��p���āA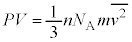 �������܂��B
�������܂��B
(2) ���`�e���̏ꍇ
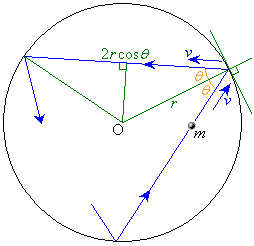 ���ar�̋��`�e��ɋC�̂���������Ă���Ƃ��܂��B
���ar�̋��`�e��ɋC�̂���������Ă���Ƃ��܂��B
�C�̕��q1��������v�Ƃ��āA�C�̕��q���e��̕ǂɏՓ˂���Ƃ��A�ՓˑO�����x�̏Փ˖ʂɐ����Ȑ����́A���x�ƏՓ˖�(�Փ˂���_�̐ڕ��ʂ��l���܂�)�̖@���Ƃ̂Ȃ��p��θ �Ƃ��āA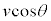 �ł��B
�ł��B
�C�̕��q1�̏ՓˑO��ł��^���ʕω��́A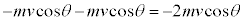
���ʕǂ��A���̋C�̕��q������͐��́A�����^���ʕω��̔���p�ŁA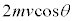
���̋C�̕��q�͋��ʕǂɏՓ˂�����A����v��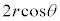 �i��Ŏ��ɋ��ʕǂɏՓ˂���̂ŁA�Փ˂���Փ˂܂ł�������
�i��Ŏ��ɋ��ʕǂɏՓ˂���̂ŁA�Փ˂���Փ˂܂ł�������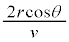 �Ct�b�ԂɁA
�Ct�b�ԂɁA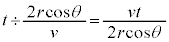 ��A���ʕǂɏՓ˂��܂��B
��A���ʕǂɏՓ˂��܂��B
�]���āA���ʕǂ�t�b�Ԃɂ��̋C�̕��q������͐��̑傫���́A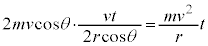
���ʕǂ��S�C�̕��q����t�b�ԂɎ��͐��̑傫���́A����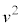 ��S�C�̕��q�ł̕��ϒl
��S�C�̕��q�ł̕��ϒl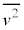 �ɒu�������āA�C�̕��q�̌�
�ɒu�������āA�C�̕��q�̌�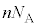 �����������̂ɂȂ�A
�����������̂ɂȂ�A �ł��B
�ł��B
���ʕǂ��S�C�̕��q��������̑傫����F�Ƃ���t�b�ԂɎ��͐��̑傫���́A
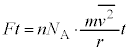
�� 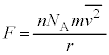 �]���āA���ʕǂ��������́A���̑傫��F�����ʂ̖ʐ�
�]���āA���ʕǂ��������́A���̑傫��F�����ʂ̖ʐ�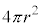 �Ŋ����āA
�Ŋ����āA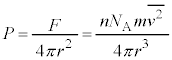
���`�e����̐�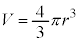 ��p���āA
��p���āA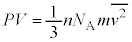 �������܂��B
�������܂��B
�ȏ�ŁA�e��̌`�����̂ł����Ă����`�ł����Ă��A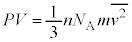 �����藧���Ƃ��킩��܂��B
�����藧���Ƃ��킩��܂��B
�Ƃ���ŁA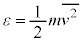 �́A�C�̕��q1�̉^���G�l���M�[�̕��ϒl�ƍl�����܂����A�����p���āA
�́A�C�̕��q1�̉^���G�l���M�[�̕��ϒl�ƍl�����܂����A�����p���āA
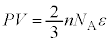 �@����A
�@����A
�������܂��B
�A�����z�C������ԕ������F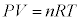 �Ɣ�r����ƁA
�Ɣ�r����ƁA
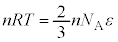 �@����B
�@����B
�����ŁA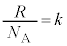 �Ƃ����ƁA
�Ƃ����ƁA
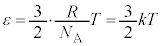 �@����C
�@����C
�ƂȂ�A�C�̕��q1�̕��ς��G�l���M�[(���̏ꍇ�́A�d�͂╪�q�Ԃɓ����͂����Ă���̂ŁA�ʒu�G�l���M�[�͂Ȃ��^���G�l���M�[�݂̂ł�)���A��Ή��x��p���āA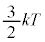 �ƕ\����邱�Ƃ��킩��܂��B
�ƕ\����邱�Ƃ��킩��܂��B
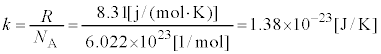
���{���c�}���萔�ƌ����܂��B�C�̒萔R�C�A�{�K�h����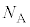 �C�{���c�}���萔k�̊ԂɁA
�C�{���c�}���萔k�̊ԂɁA
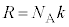
�Ƃ����W������܂��B
�܂��A�C�̕��q�̕��q��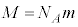 ��p���āA�C���A
��p���āA�C���A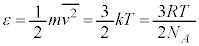 �ƂȂ�̂ŁA�C�̕��q�̕��ς̑���
�ƂȂ�̂ŁA�C�̕��q�̕��ς̑���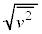 �́A
�́A
�� 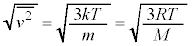
�����ŁA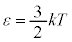 �̒��ɏo�Ă���3�Ƃ��������̈Ӗ����l���Ă݂܂��B
�̒��ɏo�Ă���3�Ƃ��������̈Ӗ����l���Ă݂܂��B
����3�̃��[�c�́A�@���E�ӂ̕����3�ł��B�ǂ����Ă�����3���o�Ă��邩�ƌ����ƁAx�������Ay�������Az��������3�������l��������ł��B�܂�A�C�̕��q���A3�����ɉ^���ł���Ƃ����Ƃ��납��o�Ă���3�ł��B���̂��Ƃ��A�C�̕��q�̉^�������R�x��3�ł���ƌ����܂��B�����ł́A�C�̕��q�������A�����A�C�̕��q��1�̌��q����ł��Ă���ƍl�����̂ŁA���R�x��3�ɂȂ�܂����B
�w���E����l�I���ł́A���q1�ŋC�̕��q�ƂȂ�܂�(�����������z�C�̂��A�P���q���q���z�C���ƌ����܂�)���A�_�f�␅�f�ł́A�_�f���q2�A���f���q2�ŋC�̕��q1�ƂȂ�܂�(�����������z�C�̂�2���q���q���z�C���ƌ����܂�)�B���q2�łł��Ă���C�̕��q�ł́A���q2���o�g���̂悤�Ȗ_������ł���Ƃ������f�����l���܂��B���̏ꍇ�ɂ́A���R�x�͉�]�^���̎��R�x2(2���q��z����ɕ���ł���Ƃ���ƁAzx���ʏ�̉�]��yz���ʏ�̉�])�����킹�āA�^�������R�x��5�ɂȂ邱�Ƃ��m���Ă��܂��B
�]���āA�P���q���q���z�C���ł́A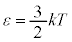
2���q���q���z�C���ł́A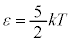
�ƂȂ�܂��B3���q�ȏォ�琬��C�̕��q�ł́A�����ƈႤ�`�ɂȂ�܂��B
�B�����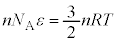 �ƂȂ�܂����A
�ƂȂ�܂����A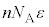 �́A�C�̕��q1���^���G�l���M�[�̕��ϒl�ɋC�̕��q�̌�
�́A�C�̕��q1���^���G�l���M�[�̕��ϒl�ɋC�̕��q�̌�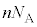 �����������̂Ȃ̂ŁA�C�̕��q�S�̂��G�l���M�[�̑��a(�����ł͈ʒu�G�l���M�[�͖�������Ă���)�ƍl�����܂��B������C�̂������G�l���M�[�ƌ����܂��B�܂�A�����̗e��ɕ������ꂽ�C�̂������G�l���M�[U�́A
�����������̂Ȃ̂ŁA�C�̕��q�S�̂��G�l���M�[�̑��a(�����ł͈ʒu�G�l���M�[�͖�������Ă���)�ƍl�����܂��B������C�̂������G�l���M�[�ƌ����܂��B�܂�A�����̗e��ɕ������ꂽ�C�̂������G�l���M�[U�́A
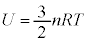
�ł��B������A�P���q���q���z�C�̂�2���q���q���z�C�̂ł́A�قȂ�`�ɂȂ�A
�P���q���q���z�C���ł́A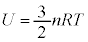
2���q���q���z�C���ł́A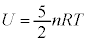
�ƂȂ�܂��B
�M�͊w���@���F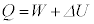 �ɂ����āA��ϕω��̏ꍇ�ɂ́A
�ɂ����āA��ϕω��̏ꍇ�ɂ́A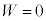 �ƂȂ�܂����A���̏ꍇ�A��σ�����M�̎��F
�ƂȂ�܂����A���̏ꍇ�A��σ�����M�̎��F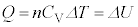 �ƁA
�ƁA
�P���q���q���z�C���ł́A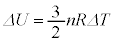
2���q���q���z�C���ł́A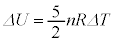
�Ƃ��r���āA��σ�����M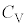 �́A
�́A
�P���q���q���z�C���ł́A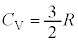
2���q���q���z�C���ł́A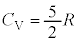
�ł��邱�Ƃ��킩��܂��B�����G�l���M�[U�́A�P���q���q���z�C�́A2���q���q���z�C�̂Ȃǂ��܂Ƃ߂āA��σ�����M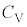 ��p���āA
��p���āA
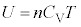
�ƂȂ�܂��B�P�Ɂu���z�C�́v�̓����G�l���M�[�Ƃ����ꍇ�ɂ́A���̎���p���܂��B
���D��L�̋C�̕��q�̎��R�x��f �Ƃ��āA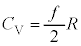 �ƂȂ邱�Ƃ��\������A�w���E��He�C�A���S��Ar�Ȃǂ̒P���q���q�C���f
�ƂȂ邱�Ƃ��\������A�w���E��He�C�A���S��Ar�Ȃǂ̒P���q���q�C���f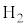 �C�_�f
�C�_�f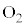 �C���f
�C���f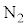 �Ȃǂ�2���q���q�ł́A��σ�����M�̎����l�Ƌ߂��̂ł����A3���q���q�ȏ�̕��q�ɂȂ�ƁA���i�^���A��]�^���̑��ɕ��q���̐U����S���̉e���Ȃǂ�����ݕ��G�ɂȂ�܂��B
�Ȃǂ�2���q���q�ł́A��σ�����M�̎����l�Ƌ߂��̂ł����A3���q���q�ȏ�̕��q�ɂȂ�ƁA���i�^���A��]�^���̑��ɕ��q���̐U����S���̉e���Ȃǂ�����ݕ��G�ɂȂ�܂��B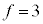 �̂Ƃ���
�̂Ƃ���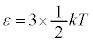 �C
�C �̂Ƃ���
�̂Ƃ���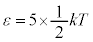 ����A�C�̕��q�����ω^���G�l���M�[��
����A�C�̕��q�����ω^���G�l���M�[��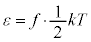 �ƌ��āA1���R�x�ɂ���
�ƌ��āA1���R�x�ɂ���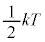 ���G�l���M�[�����z����Ă���ƍl���܂��B������G�l���M�[�����z���ƌ����܂��B
���G�l���M�[�����z����Ă���ƍl���܂��B������G�l���M�[�����z���ƌ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 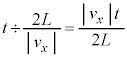 ��Ayz���ʂƏՓ˂��܂��B
��Ayz���ʂƏՓ˂��܂��B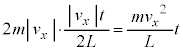
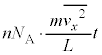 �ł��B
�ł��B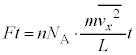
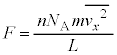
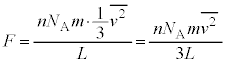
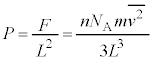
 �ł��B
�ł��B