���̐U��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�o�C�I�����A�M�^�[�A�ՁA�n�[�v�A�s�A�m�Ȃǂ̊y��́A�����U�����邱�Ƃɂ���ĉ��g���o�܂��B���������y��ł́A���[���Œ肳�ꂽ�����A�����̖тł���������A��ł͂�������A�n���}�[�Œ@�����肵�ĉ����o���܂��B
����`���g�̑���v[m/s]�ƁA���̐����xσ[kg/m]�C���̒���T[N]�Ƃ̊W���ȒP�ɋ��߂���@�Ƃ��āA������͂ƌĂ����@���m���Ă��܂��B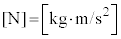 �Ȃ̂ŁAx�Cy�������Ƃ��āA����
�Ȃ̂ŁAx�Cy�������Ƃ��āA����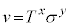 �Ƃ����W������Ƃ��܂��B���̂Ƃ��A�P�ʂɂ��Ă������W����������͂��ł��B�����ŁA
�Ƃ����W������Ƃ��܂��B���̂Ƃ��A�P�ʂɂ��Ă������W����������͂��ł��B�����ŁA
�e�P�ʂ��Ƃɍ��ӂƉE�ӂ��r����ƁA
�����������āA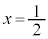 �C
�C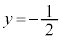 �C�]���āA
�C�]���āA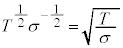 ���Av�CT�Cσ�̊Ԃɂ́A
���Av�CT�Cσ�̊Ԃɂ́A
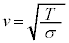 �@����@
�@����@
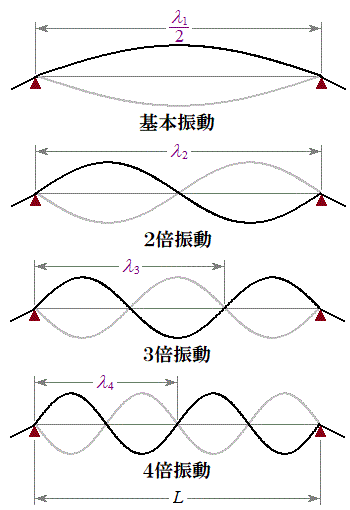 ����L�̌��̐U���́A���̗��[���Œ肳��Ă����Œ�[�ɂȂ邽�߁A�U���̗l�q�͉E�}�̂悤�ɂȂ�܂��B�e�_�ł̕ψʂ��ő�ƂȂ�u�Ԃ̌����ŁA�������甼������̌��𔖐��ŕ`���Ă��܂��B�ł��ȒP�Ȕg�`�́A�Œ�[�ɂȂ��Ă��錷�̗��[�̂ݐ߂ɂȂ���̂ŁA�������{�U���ƌ����܂��B�g�̔g����
����L�̌��̐U���́A���̗��[���Œ肳��Ă����Œ�[�ɂȂ邽�߁A�U���̗l�q�͉E�}�̂悤�ɂȂ�܂��B�e�_�ł̕ψʂ��ő�ƂȂ�u�Ԃ̌����ŁA�������甼������̌��𔖐��ŕ`���Ă��܂��B�ł��ȒP�Ȕg�`�́A�Œ�[�ɂȂ��Ă��錷�̗��[�̂ݐ߂ɂȂ���̂ŁA�������{�U���ƌ����܂��B�g�̔g����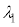 �Ƃ���ƁA�E�}���A
�Ƃ���ƁA�E�}���A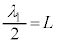 �C��
�C�� 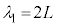
������A�@�ƌ���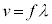 (�g�̌������Q��)��p���āA��{�U���̐U����
(�g�̌������Q��)��p���āA��{�U���̐U����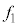 �́A
�́A
�E�}��2�{�U���ł͗��[�̑��Ɍ��̒����ɂ��߂��ł��܂��B�g���́A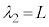 �ƂȂ�A2�{�U���̐U����
�ƂȂ�A2�{�U���̐U����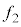 �́A
�́A
�ƂȂ�A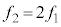 �ƂȂ��Ă��܂��B2�{�U���Ƃ����̂͂��̂��߂ł��B
�ƂȂ��Ă��܂��B2�{�U���Ƃ����̂͂��̂��߂ł��B
�E�}��3�{�U���ł͗��[�̑��ɐ߂�2�ł��܂��B�g���́A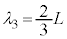 �ƂȂ�A3�{�U���̐U����
�ƂȂ�A3�{�U���̐U����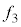 �́A
�́A
4�{�U���ł́A�g����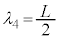 �C�U����
�C�U����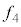 �́A
�́A
n�����R���Ƃ��āAn�{�U���ł́A�g����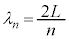 �C�U����
�C�U����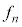 �́A
�́A
�ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B