�d���g�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�}�N�X�E�F���̕������F
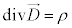 �@����@
�@����@
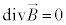 �@����A
�@����A
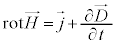 �@����B
�@����B
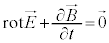 �@����C
�@����C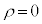 �C�d�����x
�C�d�����x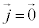 �Ƃ��܂��B�@�́A
�Ƃ��܂��B�@�́A
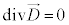 �@����D
�@����D
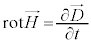 �@����E
�@����E
�E�����ӂ�rot (��]���Q��)���Ƃ�ƁA
�ƂȂ�܂����A�E�ӂ́A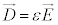 �C
�C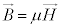 �ƇC�����A
�ƇC�����A
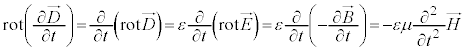 �@����F
�@����F
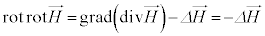 �@(�� �A���A
�@(�� �A���A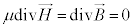 )�@����G
)�@����G
�F�C�G���A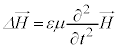 �@����H
�@����H
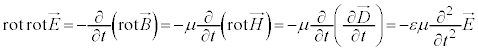 �܂��A
�܂��A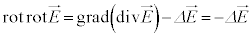 �@(�� �D���A
�@(�� �D���A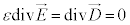 )����āA
)����āA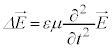 �@����I
�@����I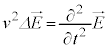 �̌`�̕��������g���������ƌ����܂�)�ɏ]�����Ƃ��킩��܂��B
�̌`�̕��������g���������ƌ����܂�)�ɏ]�����Ƃ��킩��܂��B
1�����ŁA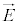 ��x�ɂ݈̂ˑ�����z����
��x�ɂ݈̂ˑ�����z����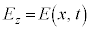 �݂̂������Ax�����Cy������0�ƂȂ�ꍇ���l���Ă݂܂��B�I�́A
�݂̂������Ax�����Cy������0�ƂȂ�ꍇ���l���Ă݂܂��B�I�́A
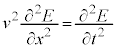 �C
�C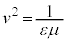 �@����J
�@����J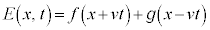 �̌`�����Ă��邱�Ƃ��m���Ă��܂��B���ۂɑ�����Ă݂�ƁA
�̌`�����Ă��邱�Ƃ��m���Ă��܂��B���ۂɑ�����Ă݂�ƁA
�ƂȂ�A�J�����Ă��邱�Ƃ��킩��܂��B
�����ŁAt���Œ肵��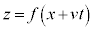 �Ƃ������̃O���t���l����ƁA
�Ƃ������̃O���t���l����ƁA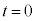 �̂Ƃ��̃O���t
�̂Ƃ��̃O���t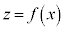 ��x����������
��x����������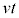 �������s�ړ������O���t��\���Ă��܂��Bt�����ԂƂ���A����v��x����������
�������s�ړ������O���t��\���Ă��܂��Bt�����ԂƂ���A����v��x����������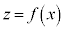 �̃O���t���ړ����邱�ƂɂȂ�܂��B���l�ɁAt���Œ肵��
�̃O���t���ړ����邱�ƂɂȂ�܂��B���l�ɁAt���Œ肵��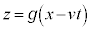 �̃O���t�́At�����ԂƂ���
�̃O���t�́At�����ԂƂ���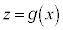 �̃O���t�𑬂�v��x���������Ɉړ��������̂ɂȂ�܂��B
�̃O���t�𑬂�v��x���������Ɉړ��������̂ɂȂ�܂��B
�J�́A �ɂ�����
�ɂ�����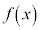 �C
�C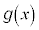 ������
������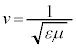 �ňړ������g�����ۂ�\���Ă����̂ł��B�H�ɂ��Ă����l��1�����ōl����Ɣg����\���܂��B�����d�E�����E�̔g�����d���g�ł��B
�ňړ������g�����ۂ�\���Ă����̂ł��B�H�ɂ��Ă����l��1�����ōl����Ɣg����\���܂��B�����d�E�����E�̔g�����d���g�ł��B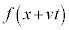 ��x���������ɐi�ޔg���őލs�g�A
��x���������ɐi�ޔg���őލs�g�A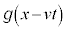 ��x���������ɐi�ޔg���Ői�s�g�ƌ����܂��B�^�ɂ����ẮA
��x���������ɐi�ޔg���Ői�s�g�ƌ����܂��B�^�ɂ����ẮA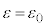 �C
�C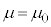 �ƍl���āA�d���g���`�d���x�́A
�ƍl���āA�d���g���`�d���x�́A
�ƂȂ�A�����Ɉ�v���܂��B���̂��Ƃ���A�����d���g�̈��ł��邱�Ƃ��킩��܂��B
3�����̏ꍇ�ɂ́A�I�̉��́A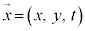 �C
�C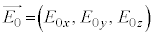 (
(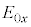 �C
�C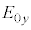 �C
�C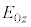 �͒萔)�C
�͒萔)�C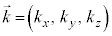 (
(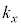 �C
�C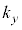 �C
�C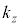 �͒萔)�Ƃ��āA
�͒萔)�Ƃ��āA
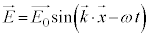 �@����K
�@����K
�ƂȂ�A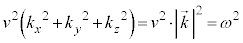 �C�܂�A
�C�܂�A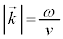 �ł���A�I�����܂��B
�ł���A�I�����܂��B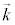 �͔g�̐i�s������\���Ă��āA
�͔g�̐i�s������\���Ă��āA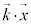 ��
��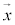 �̔g�̐i�s����������\���Ă��܂��B
�̔g�̐i�s����������\���Ă��܂��B
�D���A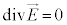 �Ȃ̂ŁA
�Ȃ̂ŁA
���ꂪ�P���I�ɐ��藧���߂ɂ́A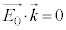 �C�����A
�C�����A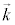 ��
��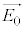 �͐����łȂ���Ȃ�܂���B�Ƃ������Ƃ́A�d�E
�͐����łȂ���Ȃ�܂���B�Ƃ������Ƃ́A�d�E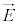 �̐U�������́A�g�̐i�s�����Ɛ����ɂȂ��Ă��āA�d�E�̔g�������g���Ƃ������Ƃ��킩��܂��B
�̐U�������́A�g�̐i�s�����Ɛ����ɂȂ��Ă��āA�d�E�̔g�������g���Ƃ������Ƃ��킩��܂��B
�S�����l�ɂ��āA�A���A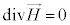 �Ȃ̂ŁA�H�̉����K�Ɠ����`�F
�Ȃ̂ŁA�H�̉����K�Ɠ����`�F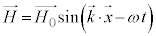 �ɏ������Ƃ��ł��āA���E�̔g�����g�̐i�s�����Ɛ����ɂȂ��Ă��āA���E�̔g�������g�ł��邱�Ƃ��킩��܂��B
�ɏ������Ƃ��ł��āA���E�̔g�����g�̐i�s�����Ɛ����ɂȂ��Ă��āA���E�̔g�������g�ł��邱�Ƃ��킩��܂��B
�K�̈ʑ�������lθ �Ƃ����ƁA
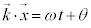 �@����L
�@����L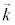 �́A���̕��ʂ̖@���x�N�g���ŁA���̕��ʂɐ����ł��B�Ƃ������Ƃ́A�d�E�����E�̔g���̐U����\���x�N�g��
�́A���̕��ʂ̖@���x�N�g���ŁA���̕��ʂɐ����ł��B�Ƃ������Ƃ́A�d�E�����E�̔g���̐U����\���x�N�g��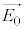 ��
��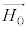 �́A����
�́A����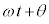 �ɑ��镽�ʇL��̃x�N�g���ɂȂ��Ă���Ƃ������Ƃł��B
�ɑ��镽�ʇL��̃x�N�g���ɂȂ��Ă���Ƃ������Ƃł��B
�܂��A�E���A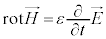 �ƂȂ�܂����A
�ƂȂ�܂����A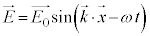 ��
��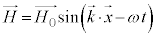 ��������ƁA
��������ƁA
���A
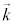 ��
��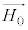 �͐����������̂ŁA
�͐����������̂ŁA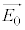 ��
��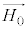 �������ɂȂ�܂�(�O�����Q��)�B�܂�A�d�E�����E�̂��ꂼ����g���̐U���̕����݂͌��ɐ����ɂȂ��Ă���Ƃ������Ƃ��킩��܂��B�܂��A�d���g�̐i�s�����́A�d�E�̐U�������������E�̐U�������ɉ��������E�˂��̌����Ƃ��āA�E�˂��̉��������Ƃ������Ƃ��킩��܂�(�E�˂��̖@�����Q��)�B
�������ɂȂ�܂�(�O�����Q��)�B�܂�A�d�E�����E�̂��ꂼ����g���̐U���̕����݂͌��ɐ����ɂȂ��Ă���Ƃ������Ƃ��킩��܂��B�܂��A�d���g�̐i�s�����́A�d�E�̐U�������������E�̐U�������ɉ��������E�˂��̌����Ƃ��āA�E�˂��̉��������Ƃ������Ƃ��킩��܂�(�E�˂��̖@�����Q��)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B