�g��������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
1�����g���������F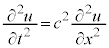
c�F�g���`�d���x
1�����g���������̈�ʉ��F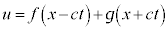
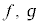 �͔C�ӂ̊�
�͔C�ӂ̊�
�����g�F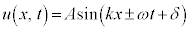 �@(�����͔g�̐i�s������\���B����x���������A����x��������)
�@(�����͔g�̐i�s������\���B����x���������A����x��������)
A�F�U���Ak�F�g���Aω�F�p�U�����Aδ�F�����ʑ�
3�����g���������F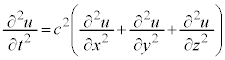
���ʔg�F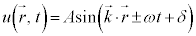 �@(
�@(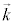 �F�g���x�N�g���B�����͔g�̐i�s������\���B����
�F�g���x�N�g���B�����͔g�̐i�s������\���B����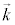 �̕����A����
�̕����A����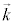 �Ƌt����)
�Ƌt����)
 ����`���1�����̔g�ŁA1�����̔g�������������߂Ă݂܂��B�E�}�̂悤��x�����Ƃ�A�����xρ�̌���x���Əd�Ȃ�Ƃ��A���ɓ���������T�Ƃ��܂��B�E�}�Ńs���N�F������
����`���1�����̔g�ŁA1�����̔g�������������߂Ă݂܂��B�E�}�̂悤��x�����Ƃ�A�����xρ�̌���x���Əd�Ȃ�Ƃ��A���ɓ���������T�Ƃ��܂��B�E�}�Ńs���N�F������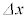 �̔�������PQ��������
�̔�������PQ��������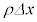 �ɂȂ�܂��B
�ɂȂ�܂��B
�E�}��P�_�Ō����ψ���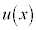 �C
�C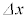 ���ꂽQ�_�Ō����ψ���
���ꂽQ�_�Ō����ψ���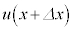 �CP�_������
�CP�_������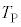 ��x���Ƃ̂Ȃ��p��α�CQ�_������
��x���Ƃ̂Ȃ��p��α�CQ�_������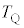 ��x���Ƃ̂Ȃ��p��β�Ƃ��܂��B�E�}�ŁA��������PQ�̕�����x���Ɛ����ȕ����Ɏ����́AP�_�Ŏ�
��x���Ƃ̂Ȃ��p��β�Ƃ��܂��B�E�}�ŁA��������PQ�̕�����x���Ɛ����ȕ����Ɏ����́AP�_�Ŏ�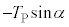 ��Q�_�Ŏ�
��Q�_�Ŏ�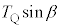 �̍��͂ŁA
�̍��͂ŁA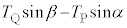 �ł��B��������PQ��x���ɐ����ȕ������^���������́A
�ł��B��������PQ��x���ɐ����ȕ������^���������́A
��������PQ��x�������ɂ͓����Ȃ��Ƃ��āAx���������͂̂肠���́A
����́A���ɓ�������T�ɓ������̂ŁA
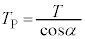 �C
�C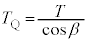
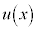 �̐ڐ��̌X���́A
�̐ڐ��̌X���́A
�_Q�ɂ�����ڐ��̌X���́A
����āA�@�́A
�ƂȂ�A���ӂ�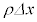 �Ŋ���ƁA
�Ŋ���ƁA
�����ŁA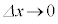 �Ƃ���ƁA
�Ƃ���ƁA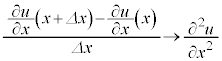 ���A
���A
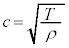 (����`���g�̓`�d���x�ł�)�Ƃ����ƁA
(����`���g�̓`�d���x�ł�)�Ƃ����ƁA
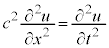 �@����A
�@����A
�Ƃ��āA
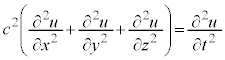 �@����B
�@����B
�A�ɁA
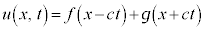 �@����C
�@����C
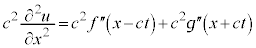
�E�ӂ́A
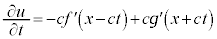 �C
�C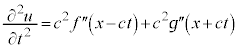
����āA�C�͇A�����܂��B�C�̂���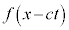 �́A
�́A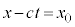 ��萔�Ƃ����
��萔�Ƃ����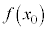 ���萔�ł��B���̂Ƃ��A
���萔�ł��B���̂Ƃ��A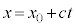 �C
�C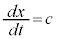 �ƂȂ�܂����A������ψ��̂Ƃ��낪���xc��x���������Ɉړ����Ă��邱�Ƃ��Ӗ����܂��B�܂�A
�ƂȂ�܂����A������ψ��̂Ƃ��낪���xc��x���������Ɉړ����Ă��邱�Ƃ��Ӗ����܂��B�܂�A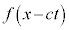 ��x���������ɐi�ޔg����\���Ă��܂��B���l�ɁA
��x���������ɐi�ޔg����\���Ă��܂��B���l�ɁA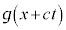 ��x���������ɐi�ޔg����\���Ă��܂��B�d���g���A�d���ꂪ�g���������A�C�B�����܂��B
��x���������ɐi�ޔg����\���Ă��܂��B�d���g���A�d���ꂪ�g���������A�C�B�����܂��B
�A�̉���ϐ��������āA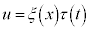 (
(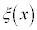 ��x�݂̂̊��A
��x�݂̂̊��A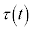 ��t �݂̂̊�)�Ƃ����A�������F
��t �݂̂̊�)�Ƃ����A�������F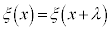 �C
�C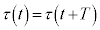 �����Ƃ��܂��B
�����Ƃ��܂��B
���A�A�́A
���ӂ�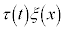 �Ŋ����āA
�Ŋ����āA
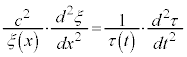 �@����D
�@����D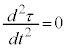 ���α�Cβ��萔�Ƃ���
���α�Cβ��萔�Ƃ���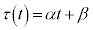 �ƂȂ�܂����A�������̏������A
�ƂȂ�܂����A�������̏������A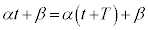 ���
���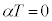 �@��
�@�� 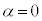 �C
�C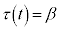
���l��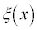 ���萔��
���萔��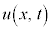 ���萔�ł��B����ł͔g���ɂȂ�܂���B
���萔�ł��B����ł͔g���ɂȂ�܂���B
�D�̒萔�����̒萔���Ƃ���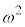 �Ƃ����ƁA
�Ƃ����ƁA
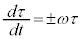 �C
�C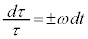 �C�ϕ����āA
�C�ϕ����āA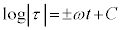 (C�F�ϕ��萔)�C
(C�F�ϕ��萔)�C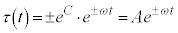 (
(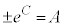 )
)
�������̏������A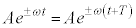 �C
�C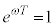 ���
���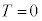
����ł͎������ɂȂ�Ȃ��̂ŁA�D�̒萔�͕��ƂȂ�A�D��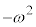 �Ƃ����ƁA
�Ƃ����ƁA
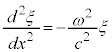 �@����E
�@����E
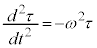 �@����F
�@����F
������A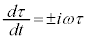 �C
�C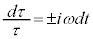 �C�ϕ����āA
�C�ϕ����āA
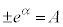 �Ƃ����ƁA
�Ƃ����ƁA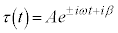 �@����G
�@����G
�G��ω��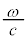 �ɂ��������āA�E�ɂ��Ă��A
�ɂ��������āA�E�ɂ��Ă��A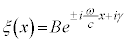 (B�Cγ�F�萔)�@����H
(B�Cγ�F�萔)�@����H
�G�́A�������̏������A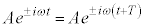 �@��
�@�� 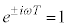 �@��
�@�� 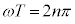 (n�F�����C
(n�F�����C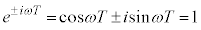 )
)
�����ł́A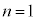 ���Ƃ��āA
���Ƃ��āA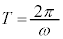 �������C
�������C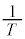 ���U�����A
���U�����A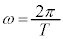 ���p�U�����ł��B
���p�U�����ł��B
�H���A�������̏������A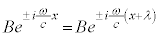 �@��
�@�� 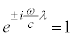 �@��
�@�� 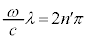 (
(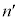 �F����)
�F����)
�������A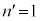 ���Ƃ��āA
���Ƃ��āA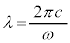 ���g���ł��B�܂��A
���g���ł��B�܂��A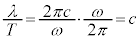 (�g�̌������Q��)�ł��B
(�g�̌������Q��)�ł��B
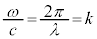 ��g���ƌ����܂��B�������āA
��g���ƌ����܂��B�������āA
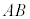 ���܂Ƃ߂�A�C
���܂Ƃ߂�A�C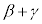 ��δ�Ƃ��Ak�̑O�̕�����k�Ɋ܂߂Ă��܂��ƁA
��δ�Ƃ��Ak�̑O�̕�����k�Ɋ܂߂Ă��܂��ƁA
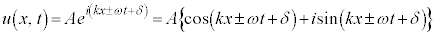 �@����I
�@����I
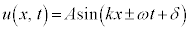 �@����J
�@����J
�I�C�J�ɂ����āA�O�q�����悤�ɁA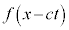 ��x���������ɐi�ޔg�A
��x���������ɐi�ޔg�A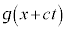 ��x���������ɐi�ޔg��\���̂ŁA
��x���������ɐi�ޔg��\���̂ŁA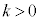 �̂Ƃ��A���������̂��̂�x���������ɐi�ޔg�A���������̂��̂�x���������ɐi�ޔg��\���܂��B�g�������ʔg�ł���ꍇ�ɂ́A�g�ʂ�x���ɐ����ł��B
�̂Ƃ��A���������̂��̂�x���������ɐi�ޔg�A���������̂��̂�x���������ɐi�ޔg��\���܂��B�g�������ʔg�ł���ꍇ�ɂ́A�g�ʂ�x���ɐ����ł��B
3�����̔g���������B�̉��́A
�܂��́A
�ŗ^�����܂��B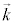 ��g���x�N�g��(
��g���x�N�g��(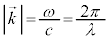 ���g���ɂȂ�܂�)�ƌ����A���̉��́A
���g���ɂȂ�܂�)�ƌ����A���̉��́A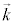 �̕����ɐi�݁A
�̕����ɐi�݁A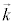 �Ɛ����ȕ����ɍL���镽�ʔg(�g�ʂ�
�Ɛ����ȕ����ɍL���镽�ʔg(�g�ʂ�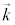 �Ɛ���)��\���܂��B�Ȃ��A���_���牓����������ɐi�ދ��ʔg(���ʔg�A���ʔg�ɂ��ẮA�z�C�w���X�̌������Q��)�́A���_�����������r�Ƃ��āA
�Ɛ���)��\���܂��B�Ȃ��A���_���牓����������ɐi�ދ��ʔg(���ʔg�A���ʔg�ɂ��ẮA�z�C�w���X�̌������Q��)�́A���_�����������r�Ƃ��āA
�ŗ^�����܂��B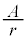 ���U���Ƃ݂�ƁA�U���͌��_����������ɔ���Ⴕ�܂��B
���U���Ƃ݂�ƁA�U���͌��_����������ɔ���Ⴕ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 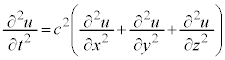
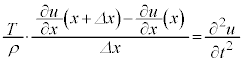
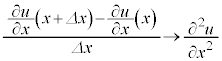 ���A
���A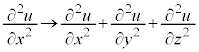
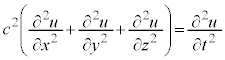 �@����B
�@����B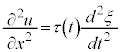 �C
�C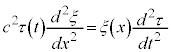
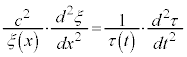 �@����D
�@����D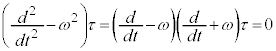
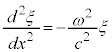 �@����E
�@����E