ホイヘンスの原理

ホイヘンスの原理　　　関連問題

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

媒質中を波動が伝わるとき、同一位相となる点を結んでできる面を波面と言う。
波面が平面である波動を平面波、波面が球面である波動を球面波と言う。
波動が伝わるとき、ある時点での波面上に並ぶ波源から発生する素元波が球面波となってできる球面群の包絡面が次の時点での波面となる、これを、ホイヘンスの原理と言う。

水面に小石を投げ込むと、小石が水中に没した点を中心とする円を描くようにして、波面ができます。円形の波面は次第に半径を大きくしながら周囲に広がっていきます。
ある1点(波源)で発生した単振動が周囲に同一の速さで伝わって行けば、山の部分、あるいは、谷の部分は、波源からの距離が等しいので、それらを連ねると、円周を描きます。これが球面波です。
船が水面を進んでいくときに、船首から両側に船が進んできた航路と鋭角を作るように直線を描いて進む波が見られます。これを船首波と言いますが、これが平面波です。
球面波も、波源から充分に遠方まで伝わって、波面の、円周あるいは球面の、半径が大きくなると、波面上の各点において、平面波として近似的に扱うことができます。
太陽光も地表のある点で観測する場合には、波源の太陽から充分に離れているので、平面波として扱います。

ある条件に従う直線の集合である直線群、あるいは、ある条件に従う曲線の集合である曲線群の全てと接するような、直線、または、曲線を、包絡線と言います。
また、ある条件に従う直線群、平面群、曲線群、曲面群の全てと接するような、平面、または、曲面を、包絡面と言います。

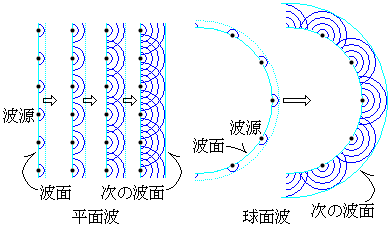ホイヘンスは、光の現象を説明するのに、次のような原理に基づいて考えることができると主張しました。
ある時点で生じている波面上に多数の波源を並べます。この波源から発生する波を素元波、または、二次波と言います。均質な媒質中であれば、一つ一つの素元波が球面波となって、同一半径の円周、または、球面となる波面を多数作ります。重ね合わせの原理によれば、これらを全て重ね合わせた波が次の時点での波面を作るはずです。ホイヘンスは、次の時点での波面は、これらの多数の円周、または、球面の包絡面になる、と、主張しました。これがホイヘンスの原理です。
右図に、平面波と球面波において、ある時点での波源から生ずる、多数の素元波が作る円周の波面と、その包絡線として生じる、次の時点での波面の様子を示しました。

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

　　物理基礎事項TOP　　物理TOP　　TOPページに戻る

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。

【広告】広告はここまでです。

苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。