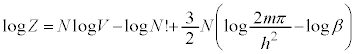���v�͊w�̊�b
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�C�̕��q�^���_�̉����Ƃ��āA�M�͊w�Ȃǂ̌��ۂ�����I�ȗ͊w���ۂ̏W���Ƃ��āA���v�I�ɑ����悤�Ƃ����u���v�͊w�v�Ƃ��������w�̕��삪����܂��B���v�͊w�̓�����̕������A������Ƃ������Ă݂܂��傤�B
�܂��A�e����̋C�̕��q���ǂ��������x���z�����Ă��邩���l���Ă݂܂��B
�e����ŋC�̕��q�͗l�X�ȕ����ɗl�X�ȑ����ʼn^�����Ă��܂��B�C�̕��q�̑��x��x�����Ay�����Az������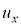 �C
�C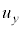 �C
�C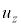 �Ƃ��āA
�Ƃ��āA
�ƂȂ�m�����l���܂��B���x�̒l�͘A���I�ɕ��z����ƍl������̂ŁA�m���́A�m�����x��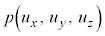 �Ƃ��čl���܂��B
�Ƃ��čl���܂��B
�m�����x���́A�S�m����1�ƂȂ�̂ŁA�e����Ŋm�����x���̐ϕ���1�ɂȂ�܂��B�e����Őϕ�����悢�̂ł����A�C�̕��q���猩��Ηe��͏[���ɑ傫���̂ŁA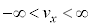 �C
�C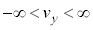 �C
�C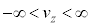 �͈̔͂Őϕ������(�̐ϕ����Q��)�A
�͈̔͂Őϕ������(�̐ϕ����Q��)�A
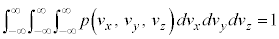 �@����@
�@����@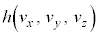 �̊��Ғl
�̊��Ғl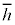 ��(���K���z���Q��)�A
��(���K���z���Q��)�A
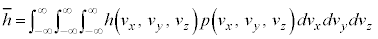 �@����A
�@����A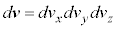 �Ƃ��āA�@�C�A���A���̂悤�ɏ����܂��B
�Ƃ��āA�@�C�A���A���̂悤�ɏ����܂��B
�@�F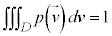
�A�F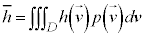
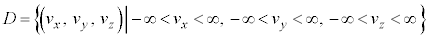 �ł��B
�ł��B
�C�̕��q�^���_�̂Ƃ��Ɠ��l�ɁA�C�̕��q�̉^���͕������������Ȃ��̂ŁA�C�̕��q��x�����̉^���Ay�����̉^���Az�����̉^�����Ɨ����Ƃ���ƁA�m���̏�@�藝�ɂ��A�m�����x��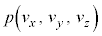 �́Ax�����Ay�����Az�����œ����`�̊m�����x��
�́Ax�����Ay�����Az�����œ����`�̊m�����x��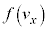 �C
�C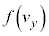 �C
�C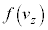 �̐ς̌`�ɏ�����͂��ł��B����āA
�̐ς̌`�ɏ�����͂��ł��B����āA
�܂��A�Ⴆ��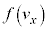 �́A�������̉^���ƕ������̉^���͑Ώ̂ɂȂ�͂��ŁA
�́A�������̉^���ƕ������̉^���͑Ώ̂ɂȂ�͂��ŁA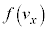 ��
��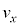 �̋���ł��B�]���āA
�̋���ł��B�]���āA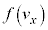 ��
��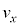 �̊����܂݂܂���B�܂�A
�̊����܂݂܂���B�܂�A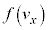 ��
��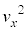 �̊��ł��B���̊������߂�
�̊��ł��B���̊������߂�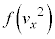 �Ə������Ƃɂ��܂��By�����Az���������l�ɍl����A
�Ə������Ƃɂ��܂��By�����Az���������l�ɍl����A
�Ƃ����`�ɏ����܂��B���l�ɍl����ƁA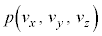 ���̂�
���̂�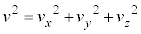 �̊�
�̊�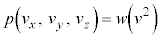 �̌`�ɕ\�����Ƃ��ł��āA
�̌`�ɕ\�����Ƃ��ł��āA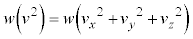 ���A
���A
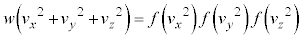 �@����B
�@����B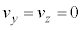 �Ƃ����ƁA
�Ƃ����ƁA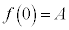 �Ƃ��āA
�Ƃ��āA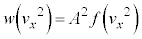
����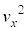 ��
��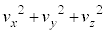 �ɓ���ւ���ƁA
�ɓ���ւ���ƁA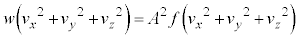
�B���A
���������f �͎w�����ł��B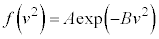 �@����C�@(�w�������G�ɂȂ邱�Ƃ��������Â炭�Ȃ�̂ŁA�w����
�@����C�@(�w�������G�ɂȂ邱�Ƃ��������Â炭�Ȃ�̂ŁA�w����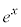 �������ł�
�������ł�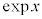 �Ə����܂�)�Ƃ������Ƃ��ł��ď㎮�ɑ������ƁA
�Ə����܂�)�Ƃ������Ƃ��ł��ď㎮�ɑ������ƁA
�ƂȂ�P���I�ɐ������܂��B������A
�@���A
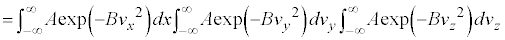
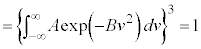 �@����D
�@����D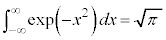 ���A�D�ɂ����āA
���A�D�ɂ����āA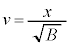 �Ƃ����ƁA
�Ƃ����ƁA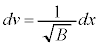 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA
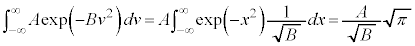 �@����E
�@����E
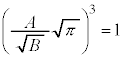 �@��
�@�� 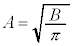
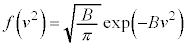
�A���A�^���G�l���M�[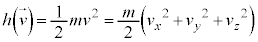 �̊��Ғl
�̊��Ғl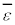 �́A
�́A
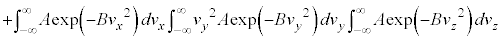
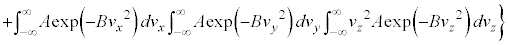 �@����F
�@����F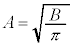 �ƇE���A
�ƇE���A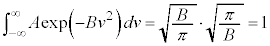
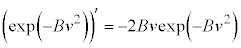 �C
�C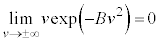 ���A�����ϕ��@��p���āA
���A�����ϕ��@��p���āA
�������F�ɑ������ƁA
�P���q���q���z�C�̂̏ꍇ�ɂ́A�C�̕��q�^���_���A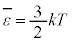 �C����āA
�C����āA
�C���A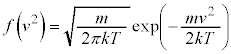
�� 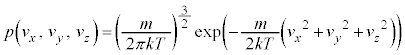 �@����G
�@����G ���ꂪ�A�P���q���q���z�C�̂̏ꍇ�̋C�̕��q�̑��x���z�ŁAMaxwell�̑��x���z�ƌĂ�Ă��܂��B�C�̕��q�̉^���ɕ��������Ȃ��ꍇ�ɂ́A���K���z�����Ă��邱�Ƃ��킩��܂��B
�����ŁA���X���������܂��B ��W�J�����Ƃ���
��W�J�����Ƃ��� �̌W���́A�������̂��܂ޏ����̐��Ƃ��āA
�̌W���́A�������̂��܂ޏ����̐��Ƃ��āA
�ƂȂ�܂��B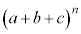 ��W�J�����Ƃ���
��W�J�����Ƃ���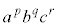 (
(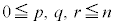 �C
�C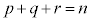 )�̌W���́A
)�̌W���́A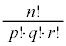 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA
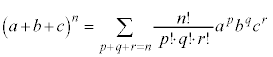 �@����H�@(
�@����H�@(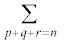 �́A
�́A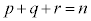 ���݂����S�Ă�
���݂����S�Ă�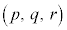 �̑g�ɂ��Ă̘a���Ӗ����܂�)
�̑g�ɂ��Ă̘a���Ӗ����܂�)
�C�̂̏�Ԃ��l����Ƃ��ɁAN�̋C�̕��q�̏�Ԃɂ��āA�̐�V�̗e���̐�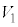 �C
�C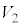 �C����C
�C����C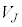 ��J�̕����ɕ����A�e�̐ς�
��J�̕����ɕ����A�e�̐ς�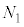 �C
�C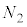 �C����C
�C����C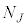 �̋C�̕��q������Ƃ���ƁA
�̋C�̕��q������Ƃ���ƁA
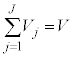 �C
�C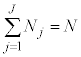
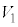 �C
�C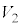 �C����C
�C����C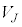 �ɋC�̕��q�����ꂼ�ꉽ���U�蕪���邩�A�Ƃ������@�̐��́A�������̂��܂ޏ����̐��ŁA
�ɋC�̕��q�����ꂼ�ꉽ���U�蕪���邩�A�Ƃ������@�̐��́A�������̂��܂ޏ����̐��ŁA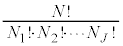 �ʂ肠��܂��B
�ʂ肠��܂��B
���̂����A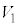 �C
�C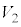 �C����C
�C����C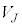 �ɐU�蕪�������
�ɐU�蕪�������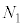 �C
�C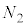 �C����C
�C����C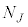 �ƂȂ�Ƃ��A�C�̕��q1����L����̐ς�
�ƂȂ�Ƃ��A�C�̕��q1����L����̐ς�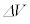 �Ƃ���ƁA�̐�
�Ƃ���ƁA�̐�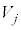 �̒���
�̒���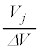 �̕������ł��܂����A
�̕������ł��܂����A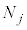 �̋C�̕��q��
�̋C�̕��q��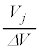 �̕����̂ǂ�ɓ��邩��
�̕����̂ǂ�ɓ��邩��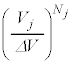 �ʂ肠��܂��B
�ʂ肠��܂��B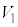 �C
�C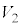 �C����C
�C����C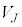 ��
��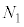 �C
�C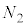 �C����C
�C����C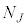 �̋C�̕��q���ǂ̂悤�ɓ��邩�͓Ɨ��Ɍ��܂�̂ŁA���̕��@�̐��́A
�̋C�̕��q���ǂ̂悤�ɓ��邩�͓Ɨ��Ɍ��܂�̂ŁA���̕��@�̐��́A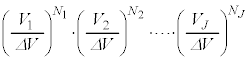 �ʂ肠��܂��B���z�C�̂̋C�̕��q���̐�V�̓����ɂǂ̂悤�ɕ��z���邩�A���̕��@�̑���W�́A
�ʂ肠��܂��B���z�C�̂̋C�̕��q���̐�V�̓����ɂǂ̂悤�ɕ��z���邩�A���̕��@�̑���W�́A
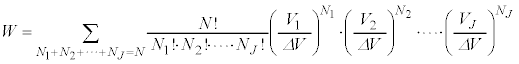 �@����I
�@����I
���A�H�Ɠ��l�ɂ��āA
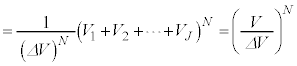 �@����J
�@����J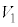 �C
�C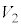 �C����C
�C����C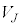 ��
��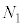 �C
�C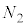 �C����C
�C����C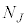 �̋C�̕��q������m���́A
�̋C�̕��q������m���́A
�J���A�S�m��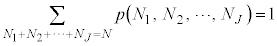 �ƂȂ�܂��B
�ƂȂ�܂��B
�M�͊w�ŋC�̂̋����ׂ�Ƃ��A�C�̕��q1�̈ʒu�A���x�ɒ��ڂ��闧�������I(microscopic)����ƌ����܂��B����ɑ��āA���́A�̐ρA���x�̂悤�ɋC�̑S�̂ɒ��ڂ��闧��������I(macroscopic)����ƌ����܂��B
�����I�Ȍ��ۂv�I�Ɉ������Ƃɂ���ċ����I�Ȍ��ۂ��l����̂����v�͊w�ł��B���v�I�Ɉ����ۂɁA�C�̕��q1�̈ʒu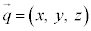 �Ɖ^����
�Ɖ^����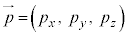 ������l���Ƃ�m�����l����̂ł����A�ʒu�Ɖ^���ʂ��A���I�Ȓl���Ƃ���̂Ƃ��āA�m�����x�����l���܂��B���̍ۂɁA6�̒l�Ax�Cy�Cz�C
������l���Ƃ�m�����l����̂ł����A�ʒu�Ɖ^���ʂ��A���I�Ȓl���Ƃ���̂Ƃ��āA�m�����x�����l���܂��B���̍ۂɁA6�̒l�Ax�Cy�Cz�C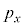 �C
�C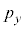 �C
�C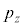 ��6�̍��W�ƌ��Ȃ��Đϕ�������s���܂��B�C�̕��q��N����A
��6�̍��W�ƌ��Ȃ��Đϕ�������s���܂��B�C�̕��q��N����A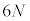 �̍��W
�̍��W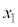 �C
�C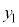 �C
�C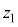 �C
�C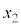 �C
�C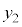 �C
�C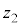 �C����C
�C����C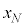 �C
�C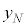 �C
�C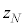 �C
�C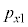 �C
�C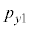 �C
�C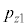 �C
�C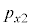 �C
�C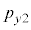 �C
�C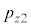 �C����C
�C����C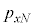 �C
�C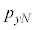 �C
�C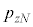 ��������̂Ƃ��čl���܂��B�������čl����
��������̂Ƃ��čl���܂��B�������čl����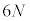 �̍��W������Ԃ��ʑ���Ԃƌ����܂��B
�̍��W������Ԃ��ʑ���Ԃƌ����܂��B
N�̋C�̕��q�̈ʒu�Ɖ^���ʂ��A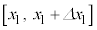 �C
�C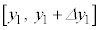 �C
�C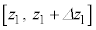 �C����C
�C����C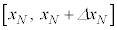 �C
�C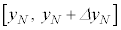 �C
�C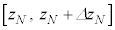 �C
�C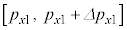 �C
�C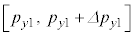 �C
�C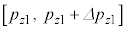 �C����C
�C����C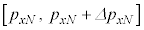 �C
�C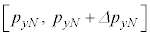 �C
�C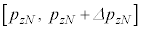 �͈̔�(
�͈̔�(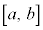 ��
��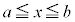 �Ƃ����͈�)�ɂ���m�����A
�Ƃ����͈�)�ɂ���m�����A
�Ƃ���ƁA�S�m����1�ɂȂ邱�Ƃ�\�����́A
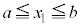 �C
�C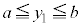 �C
�C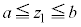 �C����C
�C����C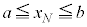 �C
�C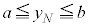 �C
�C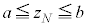
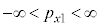 �C
�C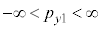 �C
�C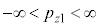 �C����C
�C����C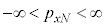 �C
�C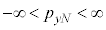 �C
�C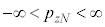
�ƒ����Ȃ��Ă��܂��̂ŁA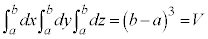 (�e��̑̐�)�ƂȂ�̂ŁA�����ł́A
(�e��̑̐�)�ƂȂ�̂ŁA�����ł́A
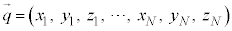 �C
�C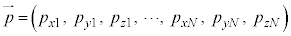 �C
�C
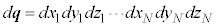 �C
�C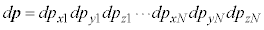 �C
�C
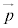 �̑��ݔ͈͂�D�Ƃ��āA
�̑��ݔ͈͂�D�Ƃ��āA
�Ə������Ƃɂ��܂��B
������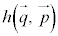 �̊��Ғl�́A
�̊��Ғl�́A
�ƂȂ�܂��B�܂��A�X�I��j�Ԗ�(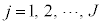 )�̃Z�����l���A���̈ʑ���ԏ�̔����̐ς�
)�̃Z�����l���A���̈ʑ���ԏ�̔����̐ς�
�Ƃ���ƁA������A
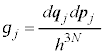 �@����K
�@����K
�n�C�[���x���O�̕s�m�萫�����F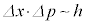
�ɏo�Ă���h�ł��B�ʑ���Ԃ��ׂ�������Ă����Ƃ��̍ŏ��P�ʂ̂悤�Ȃ��̂ł��B�������āA�I�ŁA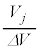 ���ʑ���Ԃ̔����̐�
���ʑ���Ԃ̔����̐�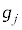 �Ƃ��A
�Ƃ��A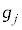 �ɓ��闱�q����
�ɓ��闱�q����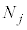 �Ƃ���ƁA
�Ƃ���ƁA
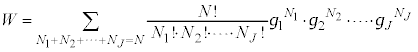 �@����L
�@����L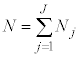
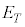 �C�S���q��N�����ł���Ƃ��܂��B���������n��micro canonical ensemble(�������W�c)�ƌ����܂��B
�C�S���q��N�����ł���Ƃ��܂��B���������n��micro canonical ensemble(�������W�c)�ƌ����܂��B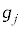 �ɓ��闱�q�����G�l���M�[��
�ɓ��闱�q�����G�l���M�[��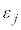 �Ƃ���ƁA
�Ƃ���ƁA
�X�^�[�����O�̌���(�K�i���ƕs�������Q��)�F ��p���ćL��ό`����ƁA
��p���ćL��ό`����ƁA
���̂Ƃ��AW�ő�ƂȂ�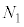 �C
�C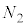 �C����C
�C����C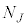 ���l���܂��B
���l���܂��B
���O�����W���̖���搔�@�Ƃ����Z�I���g����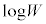 �̕ϕ����[���ɂ���m�������߂�ƁA�Z��
�̕ϕ����[���ɂ���m�������߂�ƁA�Z��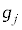 ��
��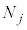 �̗��q������m��
�̗��q������m��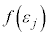 �́A
�́A
�����ŁA�S�m����1�Ƃ���ƁA
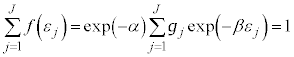 ��
�� 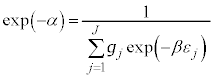
j�Ԗڂ̃Z����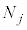 �̗��q������m����
�̗��q������m����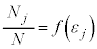 �ł��BMaxwell�̑��x���z�G�Ɣ�r����
�ł��BMaxwell�̑��x���z�G�Ɣ�r����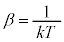 (
(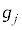 �ɓ����Ă��闱�q�̑�����
�ɓ����Ă��闱�q�̑�����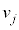 �Ƃ��āA
�Ƃ��āA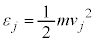 )�Ȃ̂ŁA
)�Ȃ̂ŁA
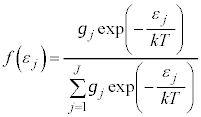 �@����M
�@����M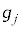 �����xT�̔M���ɐڂ��Ă��邱�Ƃ��Ӗ����Ă��܂��B���q1�̃G�l���M�[�̊��Ғl
�����xT�̔M���ɐڂ��Ă��邱�Ƃ��Ӗ����Ă��܂��B���q1�̃G�l���M�[�̊��Ғl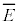 �́A
�́A
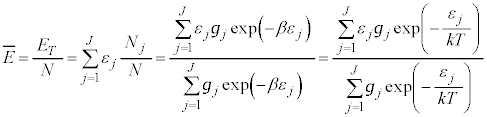 �@����N
�@����N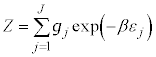 �z���ƌ����܂��B�K��p���Đϕ��\������ƁA
�z���ƌ����܂��B�K��p���Đϕ��\������ƁA
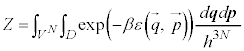 �@����O
�@����O
���D���z���O�́A�C�̕��qN����ʂł��Ȃ��Ƃ��́A��ʂł���Ƃ���N�̕��ו�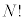 �Ŋ���K�v������܂��B���̂Ƃ��́A�O�́A
�Ŋ���K�v������܂��B���̂Ƃ��́A�O�́A 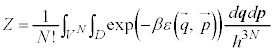 �@����P
�@����P�ƂȂ�܂��B
�����Ŋe���q����ʂł����A�e���q�̃G�l���M�[���A�^���G�l���M�[�݂̂ňʒu�ˑ������������A�e�����Ɋւ���a�̌`�ɗ^������Ƃ��A�܂�A
�̏ꍇ�ɂ́A
�����ɁA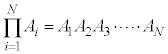 �ł��B����ɁA
�ł��B����ɁA
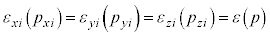 (
(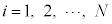 )�@����Q
)�@����Q
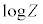 ��β�Ŕ�������ƁA
��β�Ŕ�������ƁA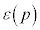 �����x�ˑ���(
�����x�ˑ���(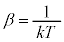 )��������
)��������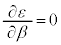 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A
�����ŁA
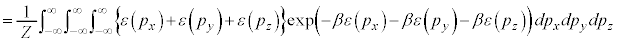
�́A���q1�̕��ς̉^���G�l���M�[�ł��B�����ł́A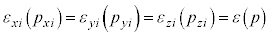 (
(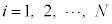 )�Ƃ����̂ŁAN�̗��q�̕��ω^���G�l���M�[��
)�Ƃ����̂ŁAN�̗��q�̕��ω^���G�l���M�[��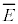 �Ɉ�v���܂��B����āA
�Ɉ�v���܂��B����āA
���q�̃G�l���M�[�̑��a�A�n�̑S�G�l���M�[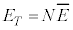 �́A�C�̂̓����G�l���M�[U�ł��B������A
�́A�C�̂̓����G�l���M�[U�ł��B������A
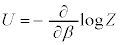 �@����R
�@����R
�P���q���q���z�C�̂ł́A���q�ԑ��ݍ�p�����āA���q�̕��i�^���̉^���G�l���M�[�݂̂��l���A
�Ƃ���ƁA����́A�ʒu�ˑ����������܂���B�P����L�Ɠ��l�ɂ���(�P���q���q���z�C�̂ł͋�̓I�Ɍv�Z�ł��܂�)�A���z��Z�́A
�����ŁA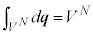 �C�܂��A
�C�܂��A
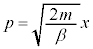 �Ƃ����ƁA
�Ƃ����ƁA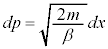 ���A���K���z���̐ϕ�������p���āA
���A���K���z���̐ϕ�������p���āA
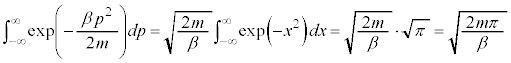 ��
�� 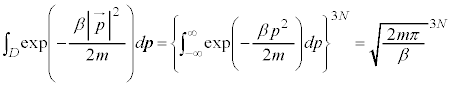
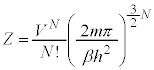 �@����S
�@����S���D���ݍ�p�̂Ȃ�N�̓��헱�q����Ȃ�n�̕��z���́A1���q�̕��z����z�Ƃ��Ĉ�ʂɁA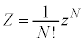 �̌`�ɕ\���܂��B
�̌`�ɕ\���܂��B
N�̓��헱�q����Ȃ�P���q���q���z�C�̕��z���̑ΐ��́A
�R���A
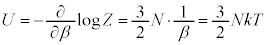 (
(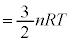 )
)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 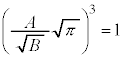 �@��
�@�� 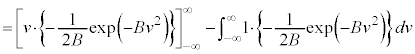
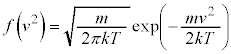
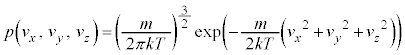 �@����G
�@����G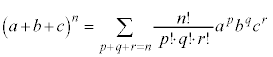 �@����H�@(
�@����H�@(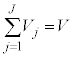 �C
�C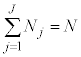
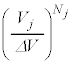 �ʂ肠��܂��B
�ʂ肠��܂��B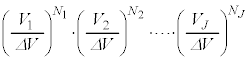 �ʂ肠��܂��B���z�C�̂̋C�̕��q���̐�V�̓����ɂǂ̂悤�ɕ��z���邩�A���̕��@�̑���W�́A
�ʂ肠��܂��B���z�C�̂̋C�̕��q���̐�V�̓����ɂǂ̂悤�ɕ��z���邩�A���̕��@�̑���W�́A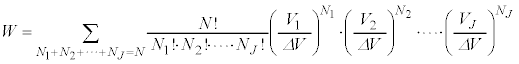 �@����I
�@����I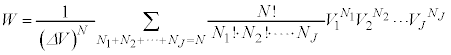
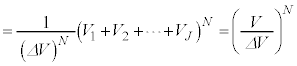 �@����J
�@����J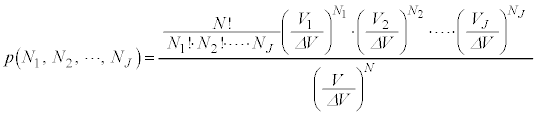
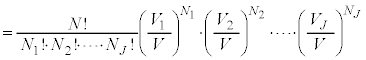
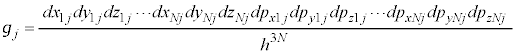
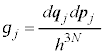 �@����K
�@����K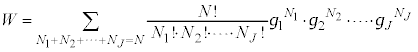 �@����L
�@����L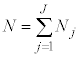
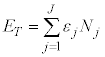
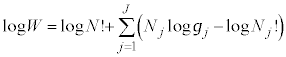
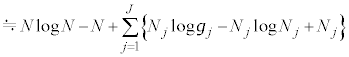
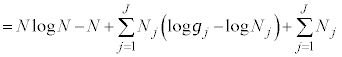
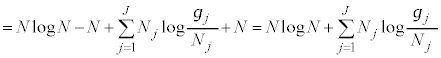
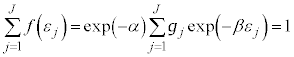
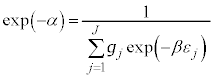
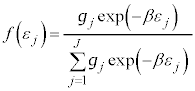
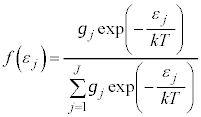 �@����M
�@����M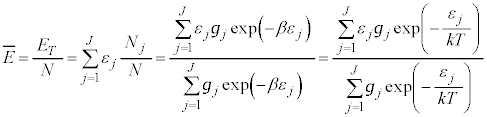 �@����N
�@����N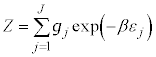 �z���ƌ����܂��B�K��p���Đϕ��\������ƁA
�z���ƌ����܂��B�K��p���Đϕ��\������ƁA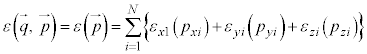
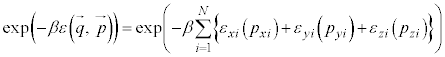
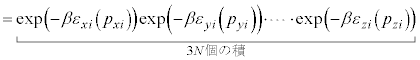
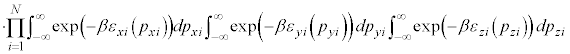
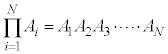 �ł��B����ɁA
�ł��B����ɁA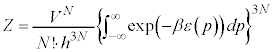
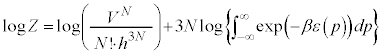
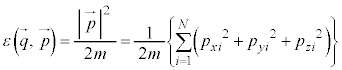
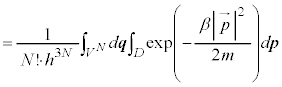
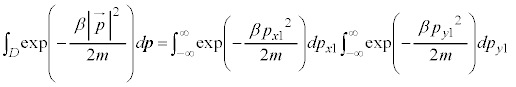
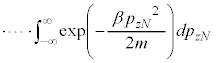
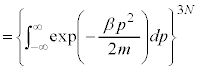
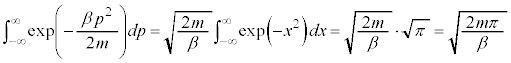
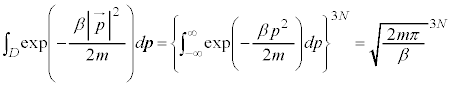
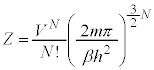 �@����S
�@����S