���K���z�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
����_���Ŏ��n���ꂽ�g�}�g973�̏d�ʂ��v�������Ƃ���A���̕\�̂悤�ɂȂ����Ƃ��܂��B
| �K��(g) | �K���l | �x�� | ���Γx�� |
| 100�ȏ�`120���� | 110 | 17 | 0.0175 |
| 120�ȏ�`140���� | 130 | 158 | 0.1624 |
| 140�ȏ�`160���� | 150 | 439 | 0.4512 |
| 160�ȏ�`180���� | 170 | 267 | 0.2744 |
| 180�ȏ�`200���� | 190 | 81 | 0.0832 |
| 200�ȏ�`220���� | 210 | 11 | 0.0113 |
| �@�v�@ | �@ | 973 | 1.0000 |
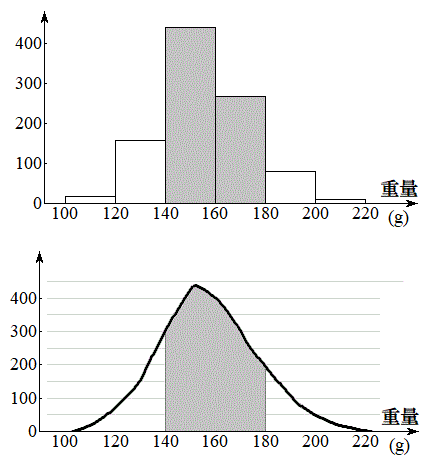 �\���̑��Γx�����K���lX�ɑ����m���ƍl����ƁA���̕\�͈���m�����z��^���܂��B
�\���̑��Γx�����K���lX�ɑ����m���ƍl����ƁA���̕\�͈���m�����z��^���܂��B
�����Ƀg�}�g�̏d�ʂ��Ƃ�A�c���ɑ��Γx�����Ƃ��āA���̕\�̃q�X�g�O������`���ƁA�E�}�̂悤�ɂȂ�܂����A�g�}�g�̎���X��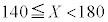 �ƂȂ�m��0.7256�́A�E��}�̊D�F���F���̖ʐςɂȂ�܂��B
�ƂȂ�m��0.7256�́A�E��}�̊D�F���F���̖ʐςɂȂ�܂��B
�g�}�g�̌��𑝂₵�A�K�����ׂ������čs���ƁA�q�X�g�O�����͎���ɘA���ȋȐ��ɋ߂Â��Ă����܂��B
�����ŁA�m���ϐ�X���A���Ȓl���Ƃ�Ƃ��āA�m�����z��\���Ȑ�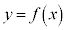 ���l���A����
���l���A����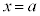 �C����
�C����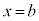 �C�Ȑ�
�C�Ȑ�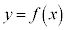 �Cx���ň͂܂�镔��(�E���}�̊D�F���F���A
�Cx���ň͂܂�镔��(�E���}�̊D�F���F���A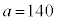 �C
�C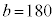 )���ʐ���
)���ʐ���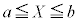 �ƂȂ�m���Ƃ��܂��B���̋Ȑ�
�ƂȂ�m���Ƃ��܂��B���̋Ȑ�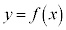 �z�Ȑ��ƌ����܂����A��`���
�z�Ȑ��ƌ����܂����A��`���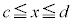 �Ƃ��āA�ȉ��̂悤�Ȑ����������܂��B
�Ƃ��āA�ȉ��̂悤�Ȑ����������܂��B
(i) �S���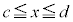 �ɂ�����
�ɂ�����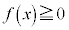 (ii)
(ii) 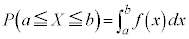 (��ϕ����Q��)
(��ϕ����Q��)
(iii) 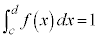
���̂Ƃ��AX��A���^�m���ϐ��A�m�����z��A���^�m�����z�A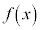 ���m�����x���ƌ����܂��B
���m�����x���ƌ����܂��B
�܂��A��L�̘A���^�m�����z�ɂ��āA���Ғl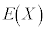 �A���U
�A���U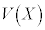 ���ȉ��̂悤�ɒ�`���܂��B
���ȉ��̂悤�ɒ�`���܂��B
�W�����́A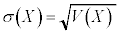 �ł��B
�ł��B
�A���^�m�����z�̒��ŁA�m�����x�����A
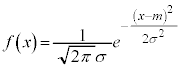 �@����@
�@����@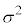 )�ƂȂ�܂����A��������K���z�ƌ����A
)�ƂȂ�܂����A��������K���z�ƌ����A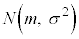 �ƕ\���܂��B
�ƕ\���܂��B
���ɁA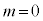 �C
�C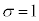 �Ƃ���
�Ƃ���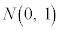 ���W�����K���z�ƌ����܂��B�W�����K���z�̊m�����x���́A
���W�����K���z�ƌ����܂��B�W�����K���z�̊m�����x���́A
�ł��B
�m���ϐ�X�����K���z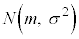 �ɏ]���Ƃ��A�m���ϐ�
�ɏ]���Ƃ��A�m���ϐ�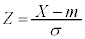 �́A�@�ɂ����āA
�́A�@�ɂ����āA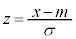 �Ƃ������Ƃɂ��A�m�����x�����A
�Ƃ������Ƃɂ��A�m�����x�����A
�Ƃ��āA�W�����K���z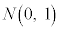 �ɏ]���܂��B
�ɏ]���܂��B
�W�����K���z���l���闝�R�́A���ȏ����̑���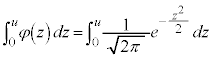 �̒l�̕\(�u���K���z�\�v�ƌ����܂�)���f�ڂ���Ă��āA���̕\�𗘗p���邱�Ƃɂ��A�قڐ��K���z�ɏ]���ƌ��Ȃ���鎖�ۂɂ��Ċm�����v�Z���邱�Ƃ��ł��邩��ł��B
�̒l�̕\(�u���K���z�\�v�ƌ����܂�)���f�ڂ���Ă��āA���̕\�𗘗p���邱�Ƃɂ��A�قڐ��K���z�ɏ]���ƌ��Ȃ���鎖�ۂɂ��Ċm�����v�Z���邱�Ƃ��ł��邩��ł��B
�Ⴆ�A�ŏ��Ɍf�������n���ꂽ�g�}�g�̏d�ʂł����A���ꂼ��̊K���ɂ�����l�𒆉��l�ő�\�����ĕ��ςƕ��U�����߂�ƁA���ς�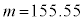 �C���U��
�C���U��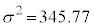 (�W������
(�W������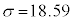 )�ƂȂ�܂��B�g�}�g�̏d��X�����K���z
)�ƂȂ�܂��B�g�}�g�̏d��X�����K���z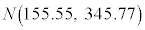 �ɏ]���A����ɂ́A
�ɏ]���A����ɂ́A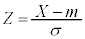 ���W�����K���z
���W�����K���z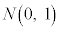 �ɏ]���A�Ƃ��čl����ƁA
�ɏ]���A�Ƃ��čl����ƁA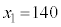 �C
�C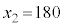 �ɑ��āA
�ɑ��āA
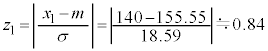 �C
�C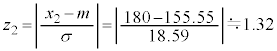
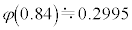 (
(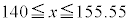 �ƂȂ�m��)�C
�ƂȂ�m��)�C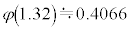 (
(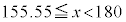 �ƂȂ�m��)�ƂȂ�̂ŁA���K���z�Ƃ��čl�����Ƃ��ɁA�g�}�g�̏d�ʂ�140g�ȏ�180g�����ƂȂ�m���́A
�ƂȂ�m��)�ƂȂ�̂ŁA���K���z�Ƃ��čl�����Ƃ��ɁA�g�}�g�̏d�ʂ�140g�ȏ�180g�����ƂȂ�m���́A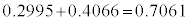 �ƂȂ�A��ɏq�ׂ��m��0.7256�Ƌ߂��l�ɂȂ�܂��B
�ƂȂ�A��ɏq�ׂ��m��0.7256�Ƌ߂��l�ɂȂ�܂��B
 n��T�C�R���𓊂���1�̖ڂ��o���X�Ƃ���ƁA�m���ϐ�X�́A���z
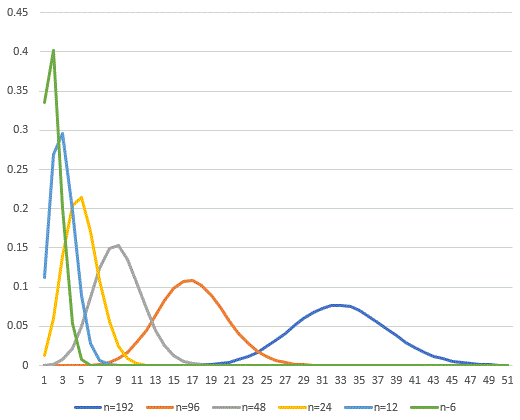
n��T�C�R���𓊂���1�̖ڂ��o���X�Ƃ���ƁA�m���ϐ�X�́A���z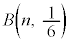 �ɏ]���܂��B�E�}�́A�\�v�Z�\�t�gEXCEL��BINOM.DIST���ƃO���t�@�\��p���āAn = 6�C12�C24�C48�C96�C192�ɂ��āA���z�̃O���t��`�������̂ł��Bn���傫���Ȃ�̂ɏ]���āA�O���t�͐��K���z�Ȑ��ɋ߂Â��Ă��܂��B
�ɏ]���܂��B�E�}�́A�\�v�Z�\�t�gEXCEL��BINOM.DIST���ƃO���t�@�\��p���āAn = 6�C12�C24�C48�C96�C192�ɂ��āA���z�̃O���t��`�������̂ł��Bn���傫���Ȃ�̂ɏ]���āA�O���t�͐��K���z�Ȑ��ɋ߂Â��Ă��܂��B
n���[���ɑ傫���ꍇ�ɂ��ẮA���z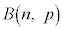 ���ߎ��I�ɐ��K���z
���ߎ��I�ɐ��K���z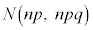 �ƍl����ƁA�m���ϐ�
�ƍl����ƁA�m���ϐ�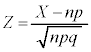 �͕W�����K���z
�͕W�����K���z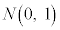 �ɏ]���̂ŁA���K���z�\��p���āA�m���Ȃǂ��v�Z���邱�Ƃ��ł��܂��B
�ɏ]���̂ŁA���K���z�\��p���āA�m���Ȃǂ��v�Z���邱�Ƃ��ł��܂��B
�Ⴆ�A384��T�C�R���𓊂���1�̖ڂ��o���X�Ƃ���ƁA�m���ϐ�X�́A���z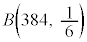 �ɏ]���܂��B���ς�
�ɏ]���܂��B���ς�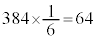 �C���U��
�C���U��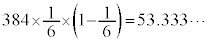 �C�W������
�C�W������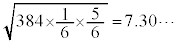 �ł��B
�ł��B
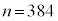 ���[���ɑ傫���ƍl���āA�m���ϐ�X�����K���z
���[���ɑ傫���ƍl���āA�m���ϐ�X�����K���z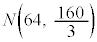 �ɏ]���ƍl���A
�ɏ]���ƍl���A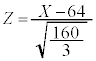 �Ƃ����Ɗm���ϐ�Z�͕W�����K���z�ɏ]���̂ŁA1�̖ڂ�70��ȏ�o��m���́A
�Ƃ����Ɗm���ϐ�Z�͕W�����K���z�ɏ]���̂ŁA1�̖ڂ�70��ȏ�o��m���́A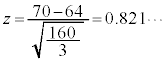 ���A���K���z�\��
���A���K���z�\��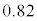 �̂Ƃ����ǂ��0.2939 (����͕��ςł���64��ȏ�ł����Ă���70��ȉ��ƂȂ�m��)�C����āA
�̂Ƃ����ǂ��0.2939 (����͕��ςł���64��ȏ�ł����Ă���70��ȉ��ƂȂ�m��)�C����āA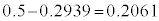 (0.5��������̂́A���ς�64��ȏ�o��m����0.5������ł�)�Ƃ��Ċm�����v�Z���邱�Ƃ��ł��܂��B
(0.5��������̂́A���ς�64��ȏ�o��m����0.5������ł�)�Ƃ��Ċm�����v�Z���邱�Ƃ��ł��܂��B
�m�����x���Ɋւ���������A���K���z�A�W�����K���z�̏ꍇ�ɂ��āA�l�@���Ă����܂��B
�ϕ�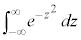 �́A�F�X�Ɠ���ȍH�v�����č��Z�͈͓̔��̒m���݂̂�p���ċ��߂悤�A�Ƃ����������͌����܂����A��ʓI���@�ł́A���Z�͈͓̔��ł͋��߂��܂���B
�́A�F�X�Ɠ���ȍH�v�����č��Z�͈͓̔��̒m���݂̂�p���ċ��߂悤�A�Ƃ����������͌����܂����A��ʓI���@�ł́A���Z�͈͓̔��ł͋��߂��܂���B
���Z�͈̔͊O�ł����A�ȉ��̂悤���d�ϕ���p���Čv�Z������@���m���Ă��܂��B
���_ �C
�C �C
�C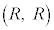 �C
�C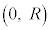 ��4�_��4���_�Ƃ��鐳���`S�́A���_�𒆐S�Ƃ��锼�aR�̉~��
��4�_��4���_�Ƃ��鐳���`S�́A���_�𒆐S�Ƃ��锼�aR�̉~��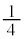 (
(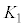 �Ƃ��܂�)���܂�ł��āA���_�𒆐S�Ƃ��锼�a
�Ƃ��܂�)���܂�ł��āA���_�𒆐S�Ƃ��锼�a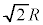 �̉~��
�̉~��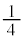 (
(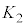 �Ƃ��܂�)�ɂ͊܂܂�܂��B�]���āAS���
�Ƃ��܂�)�ɂ͊܂܂�܂��B�]���āAS���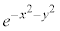 �̐ϕ��́A
�̐ϕ��́A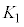 ��ł̐ϕ������傫���A
��ł̐ϕ������傫���A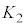 ��ł̐ϕ������������Ȃ�܂��B����āA
��ł̐ϕ������������Ȃ�܂��B����āA
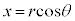 �C
�C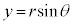 �Ƃ���ƁA
�Ƃ���ƁA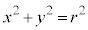 �C
�C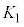 �ł́A
�ł́A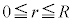 �C
�C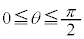 �C
�C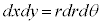 (�������W�n�E�~�����W�n�E�����W�n���Q��)���A
(�������W�n�E�~�����W�n�E�����W�n���Q��)���A
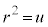 �Ƃ����ƁA
�Ƃ����ƁA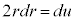 �Cr�F0��R�̂Ƃ��Au�F0��
�Cr�F0��R�̂Ƃ��Au�F0��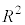 ���A
���A
���l�ɁA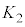 �ł́A
�ł́A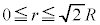 �C
�C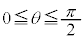 �Ȃ̂ŁA
�Ȃ̂ŁA
�܂��AS�ł́A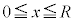 �C
�C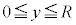 ���A
���A
������A
�����ŁA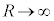 �Ƃ���ƁA���Ӂ�
�Ƃ���ƁA���Ӂ�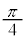 �C�E�Ӂ�
�C�E�Ӂ�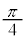 �C�͂��݂����̌������A
�C�͂��݂����̌������A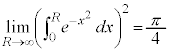
����āA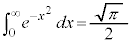 �C
�C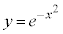 �͋���Ȃ̂ŁA
�͋���Ȃ̂ŁA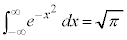
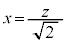 �Ƃ����ƁA
�Ƃ����ƁA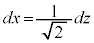
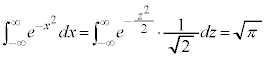 �@��
�@�� 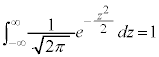 �@����A
�@����A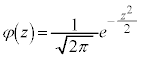 �́A�m�����x���̏��������܂��B
�́A�m�����x���̏��������܂��B
�A�ɂ����āA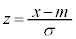 �Ƃ����ƁA
�Ƃ����ƁA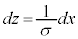
������A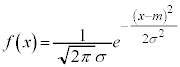 �@����@�@�́A�m�����x���̏��������܂��B
�@����@�@�́A�m�����x���̏��������܂��B
�m���ϐ�X���A���Ȓl���Ƃ�Ƃ��A�m�����z��\���Ȑ�(���z�Ȑ�)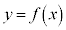 ���l���A
���l���A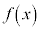 �̒�`���
�̒�`���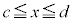 �Ƃ��āA�ȉ��̂悤�Ȑ��������Ƃ��A�m�����z��A���^�m�����z�ƌ����B
�Ƃ��āA�ȉ��̂悤�Ȑ��������Ƃ��A�m�����z��A���^�m�����z�ƌ����B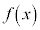 ����Ɋm�����x���ƌ����B
����Ɋm�����x���ƌ����B
(i) �S���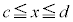 �ɂ�����
�ɂ�����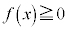 (ii)
(ii) 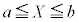 �ƂȂ�m���F
�ƂȂ�m���F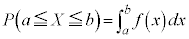 (iii)
(iii) 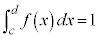
���̂Ƃ��A�m���ϐ�X�̕���(���Ғl)�F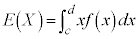 (
(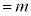 �Ƃ���)�C�m���ϐ�X�̕��U�F
�Ƃ���)�C�m���ϐ�X�̕��U�F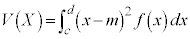 �C�m���ϐ�X�̕W�����F
�C�m���ϐ�X�̕W�����F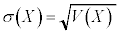
�A���^�m�����z�ŁA�m�����x����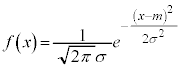 (��`��͑S����)�ƂȂ���̂��A���K���z�ƌ����B���ς�m�C�W������σ�C���̐��K���z��
(��`��͑S����)�ƂȂ���̂��A���K���z�ƌ����B���ς�m�C�W������σ�C���̐��K���z��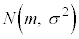 �ƕ\���B
�ƕ\���B
���ɁA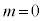 �C
�C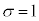 �ƂȂ鐳�K���z
�ƂȂ鐳�K���z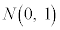 ��W�����K���z�ƌ����B�W�����K���z�̊m�����x���́A
��W�����K���z�ƌ����B�W�����K���z�̊m�����x���́A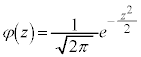
�W�����K���z�ŁAu�̒l��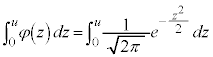 �̒l(�m��
�̒l(�m��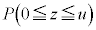 �ɂȂ�)�Ƃ̑Ή��\�𐳋K���z�\�ƌ����B
�ɂȂ�)�Ƃ̑Ή��\�𐳋K���z�\�ƌ����B
�m���ϐ�X�����K���z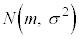 �ɏ]���Ƃ��A�m���ϐ�
�ɏ]���Ƃ��A�m���ϐ�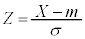 �́A�W�����K���z
�́A�W�����K���z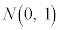 �ɏ]���B
�ɏ]���B
n���[���ɑ傫���Ƃ��A���z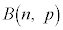 ���ߎ��I�ɐ��K���z
���ߎ��I�ɐ��K���z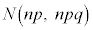 �ƍl���邱�Ƃ��ł���B�m���ϐ�
�ƍl���邱�Ƃ��ł���B�m���ϐ�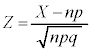 �͕W�����K���z
�͕W�����K���z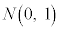 �ɏ]���B
�ɏ]���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 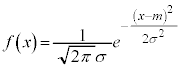 �@����@
�@����@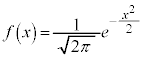
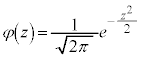
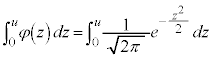 �̒l�̕\(�u���K���z�\�v�ƌ����܂�)���f�ڂ���Ă��āA���̕\�𗘗p���邱�Ƃɂ��A�قڐ��K���z�ɏ]���ƌ��Ȃ���鎖�ۂɂ��Ċm�����v�Z���邱�Ƃ��ł��邩��ł��B
�̒l�̕\(�u���K���z�\�v�ƌ����܂�)���f�ڂ���Ă��āA���̕\�𗘗p���邱�Ƃɂ��A�قڐ��K���z�ɏ]���ƌ��Ȃ���鎖�ۂɂ��Ċm�����v�Z���邱�Ƃ��ł��邩��ł��B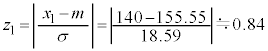 �C
�C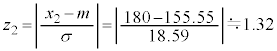
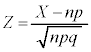 �͕W�����K���z
�͕W�����K���z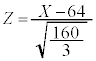 �Ƃ����Ɗm���ϐ�Z�͕W�����K���z�ɏ]���̂ŁA1�̖ڂ�70��ȏ�o��m���́A
�Ƃ����Ɗm���ϐ�Z�͕W�����K���z�ɏ]���̂ŁA1�̖ڂ�70��ȏ�o��m���́A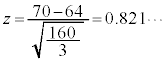 ���A���K���z�\��
���A���K���z�\��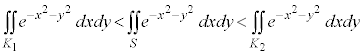
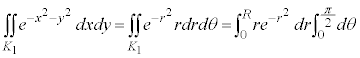
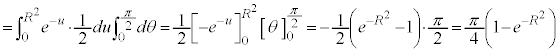
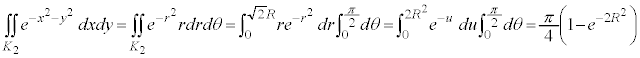
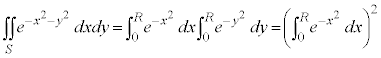
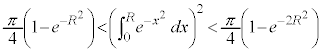
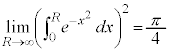
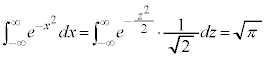 �@��
�@�� 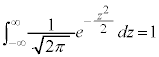 �@����A
�@����A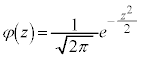 �́A�m�����x���̏��������܂��B
�́A�m�����x���̏��������܂��B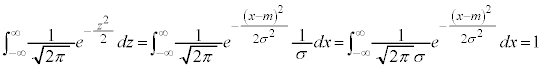
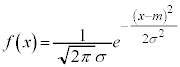 �@����@�@�́A�m�����x���̏��������܂��B
�@����@�@�́A�m�����x���̏��������܂��B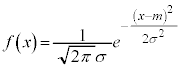 (��`��͑S����)�ƂȂ���̂��A���K���z�ƌ����B���ς�m�C�W������σ�C���̐��K���z��
(��`��͑S����)�ƂȂ���̂��A���K���z�ƌ����B���ς�m�C�W������σ�C���̐��K���z��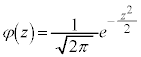
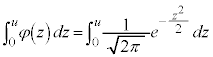 �̒l(�m��
�̒l(�m��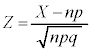 �͕W�����K���z
�͕W�����K���z