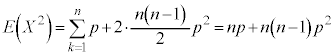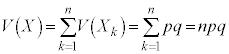���z�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
3��T�C�R���𓊂���1�̖ڂ��o���X�Ƃ���ƁA�������s�̌������A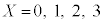 �ƂȂ�m��
�ƂȂ�m��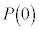 �C
�C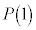 �C
�C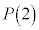 �C
�C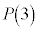 �́A
�́A
�ƂȂ�̂ŁA�ȉ��̊m�����z�̕\�������܂��B
��ʓI�ɁA1��̎��s�ɂ����āA����A���N����m����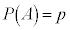 (
(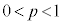 )�Ƃ��āA
)�Ƃ��āA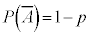 (
(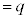 �Ƃ��܂�)�Cn�s���s���Ƃ��An��k��A���N����m��
�Ƃ��܂�)�Cn�s���s���Ƃ��An��k��A���N����m��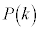 �́A�������s�̌������A
�́A�������s�̌������A
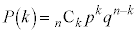 �@����@
�@����@
�A���A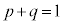 ���A
���A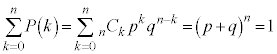 (�藝���Q��)�ɒ��ӂ��Ă��������B
(�藝���Q��)�ɒ��ӂ��Ă��������B
�\(��)�̊m�����z�����z�ƌ����A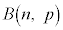 �ƕ\���܂��B
�ƕ\���܂��B
n��̎��s�̂����Ŏ���A���N�����X�Ƃ���ƁA�m���ϐ�X�͓��z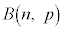 �ɏ]���܂��B
�ɏ]���܂��B
3�̃T�C�R���𓊂���1�̖ڂ��o���T�C�R���̌���X�Ƃ����m�����z�́A���z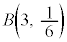 �ɂȂ�܂��B
�ɂȂ�܂��B
���z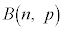 �ɏ]���m���ϐ�X�̕���
�ɏ]���m���ϐ�X�̕���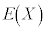 �́A�@��p���Ē�`�ʂ�Ɍv�Z����ƁA
�́A�@��p���Ē�`�ʂ�Ɍv�Z����ƁA
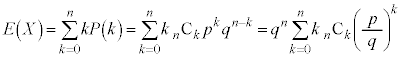 �@����A
�@����A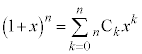 �Cx����������ƁA
�Cx����������ƁA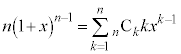
�����ŁA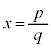 �Ƃ���ƁA
�Ƃ���ƁA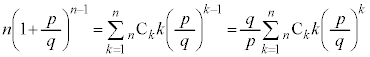
�� 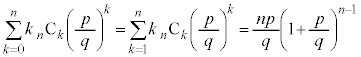 (�����̃C�R�[���́A
(�����̃C�R�[���́A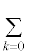 �̒���
�̒���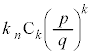 ��
��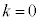 �̂Ƃ�0�Ȃ̂ŁA
�̂Ƃ�0�Ȃ̂ŁA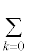 ��
��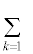 �Ƃœ������Ȃ邱�Ƃɒ���)
�Ƃœ������Ȃ邱�Ƃɒ���)
������A�ɑ�����āA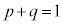 ���A
���A
�����Ƃ��Ak��ڂ̎��s�ɂ����āA����A���N����Ƃ���1�A�N����Ȃ��Ƃ���0�ƂȂ�m���ϐ���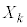 �Ƃ���ƁA
�Ƃ���ƁA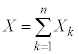 ��n��̎��s�̒��Ŏ���A���N����ł��B
��n��̎��s�̒��Ŏ���A���N����ł��B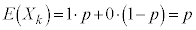 �ł����āA�u�a�̊��Ғl�͊��Ғl�̘a�v��p����ƁA
�ł����āA�u�a�̊��Ғl�͊��Ғl�̘a�v��p����ƁA
�ƊȒP��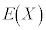 �����߂��܂��B
�����߂��܂��B
���z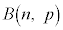 �ɏ]���m���ϐ�X�̕��U
�ɏ]���m���ϐ�X�̕��U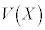 �́A���U�̌���
�́A���U�̌���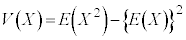 ��p���ċ��߂悤�Ƃ���ƁA
��p���ċ��߂悤�Ƃ���ƁA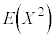 �����ł��B
�����ł��B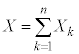 ���A
���A
�u�a�̊��Ғl�͊��Ғl�̘a�v��p����ƁA
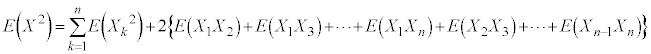 �@����B
�@����B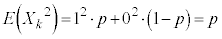 �@����C�@�ł��B
�@����C�@�ł��B
�܂��A1��ڂ̎��s��2��ڂ̎��s�ɂ��āA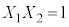 �ƂȂ�̂�
�ƂȂ�̂�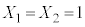 �̏ꍇ�����ł��̊m����
�̏ꍇ�����ł��̊m����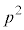 �C����
�C����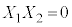 �ł��̊m����
�ł��̊m����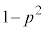 �Ȃ̂ŁA
�Ȃ̂ŁA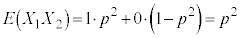 �C����
�C����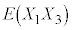 �C����C
�C����C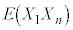 �C
�C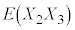 �C����C
�C����C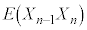 �����l�ɁA
�����l�ɁA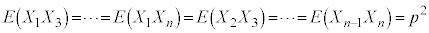
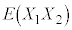 �C
�C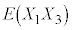 �C����C
�C����C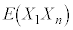 �C
�C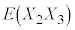 �C����C
�C����C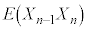 �́A�S���ŁA�قȂ�n����2��I���g�ݍ��킹�̐�
�́A�S���ŁA�قȂ�n����2��I���g�ݍ��킹�̐�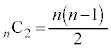 ����̂ŁA
����̂ŁA
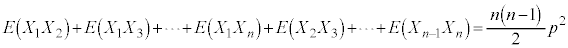 �@����D
�@����D
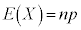 �������̂ŁA������A
�������̂ŁA������A
�ƂȂ�܂��B
������A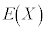 �Ɠ��l�ɁAn��̎��s�̊e��ɂ��āA
�Ɠ��l�ɁAn��̎��s�̊e��ɂ��āA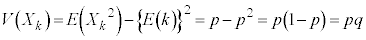
�ƂȂ�̂ŁAn��̎��s�̊e�݂��ɓƗ��ł��邱�Ƃ��l�����(�������z���Q��)�A
�Ƃ���ΊȒP�ɋ��߂��܂��B
�W�����́A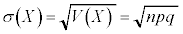 �ƂȂ�܂��B
�ƂȂ�܂��B
�m���ϐ�X�ɂ��āA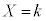 (
(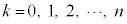 )�ƂȂ�m����
)�ƂȂ�m����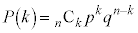 �ƂȂ�m�����z����z�ƌ����A
�ƂȂ�m�����z����z�ƌ����A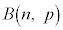 �ƕ\���B
�ƕ\���B
�m���ϐ�X�����z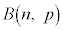 �ɏ]���Ƃ��A
�ɏ]���Ƃ��A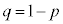 �Ƃ��āA
�Ƃ��āA
����(���Ғl)�F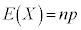 �C���U�F
�C���U�F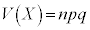 �C�W�����F
�C�W�����F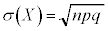
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 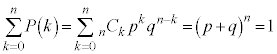 (�藝���Q��)�ɒ��ӂ��Ă��������B
(�藝���Q��)�ɒ��ӂ��Ă��������B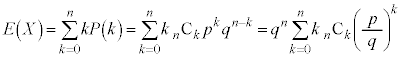 �@����A
�@����A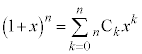 �Cx����������ƁA
�Cx����������ƁA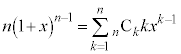
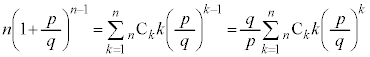
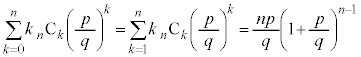 (�����̃C�R�[���́A
(�����̃C�R�[���́A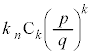 ��
��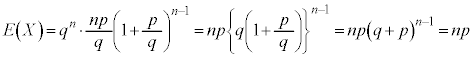
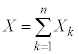 ��n��̎��s�̒��Ŏ���A���N����ł��B
��n��̎��s�̒��Ŏ���A���N����ł��B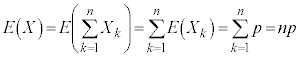
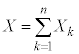 ���A
���A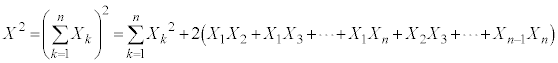
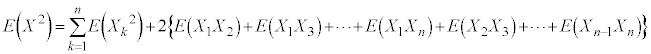 �@����B
�@����B