同時分布
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
箱の中にAと書かれたカードが3枚、Bと書かれたカードが2枚入っています。袋Aには赤球1個、白球2個、青球3個が入っており、袋Bには赤球3個、白球1個、青球2個が入っています。カード5枚を引くのは同様に確からしく、袋の中の6球を取り出すのは同様に確からしいとします。箱からカードを1枚引いて、カードに書かれている袋から球を1個取り出すとします。カードA,カードBを引くそれぞれの場合に、袋から赤球、白球、青球を取り出す確率を表にすると、以下の表(*)のようになります。
このように、Xが取り得る値、A,B,また、Yが取り得る値、赤、白、青のすべての組に対してそれぞれ確率が定まるような分布を、X,Yの同時分布と言います。
一般的に、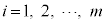 ,
,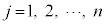 として、確率変数Xの取り得る値
として、確率変数Xの取り得る値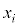 ,確率変数Yが取り得る値
,確率変数Yが取り得る値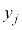 について、確率
について、確率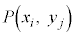 が以下の表(**)のように定まり、
が以下の表(**)のように定まり、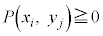 ,
,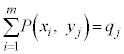 ,
,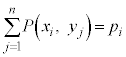 ,
,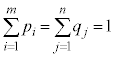 であれば、この分布がX,Yの同時分布です。
であれば、この分布がX,Yの同時分布です。
確率変数X,Yの平均(期待値)は(確率分布を参照)、
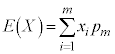 ,
,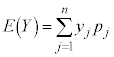
表(**)の分布に従う確率変数X,Yの和となる確率変数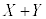 の平均(期待値)は、
の平均(期待値)は、
となります。「和の期待値は期待値の和」になっています。
また、a,bを定数として、確率変数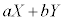 の平均(期待値)は、
の平均(期待値)は、
2つの事象A,Bにおいて、事象Aが起こるか起こらないか、ということが、事象Bの起こる確率に影響しないとき、事象Aと事象Bは互いに独立である、と言います。このとき、事象Aと事象Bがともに起こる確率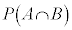 は、
は、
となります。それに対して、事象Aが起こるか起こらないか、ということが、事象Bの起こる確率に影響するとき、事象Bは事象Aに従属する、と言います。このとき、事象Aが起きたという条件の下に事象Bが起こる確率を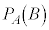 (条件付確率と言います)として、事象Aと事象Bがともに起こる確率
(条件付確率と言います)として、事象Aと事象Bがともに起こる確率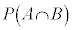 は、
は、
となります。表(*)の分布は、例えば、Aと書かれたカードを引いて赤球を取り出す確率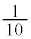 は、Aと書かれたカードを引く確率
は、Aと書かれたカードを引く確率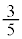 と、Aと書かれたカードを引くという条件の下に赤球を取り出す確率
と、Aと書かれたカードを引くという条件の下に赤球を取り出す確率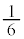 の積、つまり、
の積、つまり、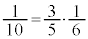 になっていて、赤球を取り出す事象が、Aと書かれたカードを引く事象に従属しています。このとき、確率変数Xと確率変数Yとは独立ではありません。
になっていて、赤球を取り出す事象が、Aと書かれたカードを引く事象に従属しています。このとき、確率変数Xと確率変数Yとは独立ではありません。
仮に、表(*)の分布で、袋Aも袋Bも袋の中に、赤球1個、白球2個、青球3個入っているとすれば、赤球を取り出す確率、白球を取り出す確率、青球を取り出す確率は、カードAを引くか引かないかに依存しなくなります。この場合には、確率変数Xと確率変数Yとは互いに独立です。
表(**)の分布で、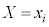 (
(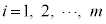 )となる事象と
)となる事象と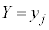 (
(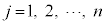 )となる事象が同時に起こるとき、この2つの事象が独立であれば、
)となる事象が同時に起こるとき、この2つの事象が独立であれば、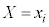 となる確率
となる確率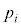 は、
は、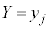 となる確率に影響せず、
となる確率に影響せず、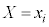 かつ
かつ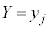 となる確率は、
となる確率は、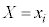 となる確率
となる確率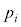 は、
は、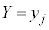 となる確率
となる確率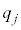 の積になります。つまり、
の積になります。つまり、
このとき、確率変数Xと確率変数Yとは互いに独立です。
表(**)の分布において、確率変数Xと確率変数Yとが互いに独立であるとき、確率変数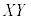 の平均(期待値)は、
の平均(期待値)は、
また、このとき、確率変数Xと確率変数Yの和となる確率変数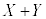 の分散は、
の分散は、
また、a,bを定数として、確率変数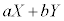 の分散は、
の分散は、
同様に、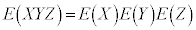 ,
,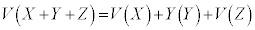 が成り立ちます。
が成り立ちます。
確率変数Xの取り得る値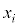 (
(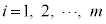 ),確率変数Yが取り得る値
),確率変数Yが取り得る値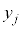 (
(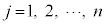 )に対して、以下の性質をもつ確率
)に対して、以下の性質をもつ確率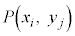 が定まるとき、この関係を同時分布と言う。
が定まるとき、この関係を同時分布と言う。
和の平均(期待値):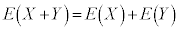 ,また、a,bを定数として、
,また、a,bを定数として、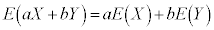
同時分布において、確率変数X,Yが独立であるとき、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
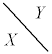
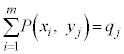 ,
,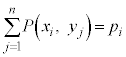 ,
,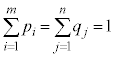 であれば、この分布がX,Yの同時分布です。
であれば、この分布がX,Yの同時分布です。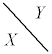
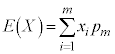 ,
,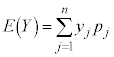
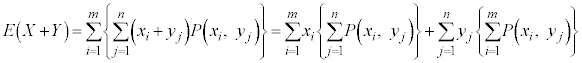
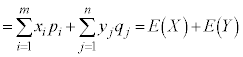
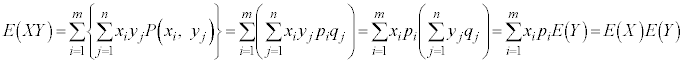
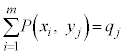 ,
,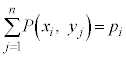 ,
,