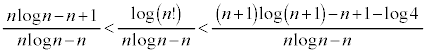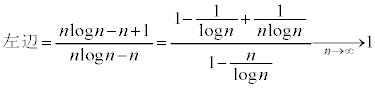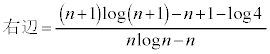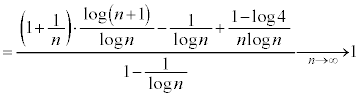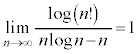�K�i���ƕs�����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
1�C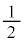 �C
�C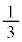 �C����C
�C����C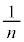 �C��� �Ƒ�������a����ƌ����܂��B���a����̑�n���܂ł̘a�F
�C��� �Ƒ�������a����ƌ����܂��B���a����̑�n���܂ł̘a�F
�@�@�@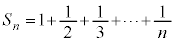
���A��ʓI��n�̎��ŕ\�����Ƃ͂ł��܂���B
�ł����A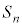 ����̂ǂꂭ�炢�̐��Ȃ̂��ׂ���@������܂��B
����̂ǂꂭ�炢�̐��Ȃ̂��ׂ���@������܂��B
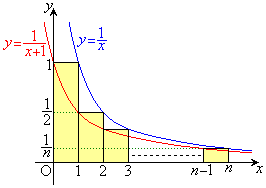 �E�}�ɂ����āA���F�œh��ꂽ�����̖ʐς̘a�́A
�E�}�ɂ����āA���F�œh��ꂽ�����̖ʐς̘a�́A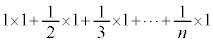 �ƂȂ�A���a����̑�n���܂ł̘a
�ƂȂ�A���a����̑�n���܂ł̘a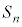 �ɂȂ�܂��B
�ɂȂ�܂��B
���̖ʐς́A�Ȑ��F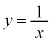 �ƒ���
�ƒ���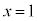 �C����
�C����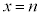 �Cx���Ƃň͂܂ꕔ���̖ʐς�1 (�E�}��
�Cx���Ƃň͂܂ꕔ���̖ʐς�1 (�E�}��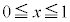 �̕����ɑ��݂���l�p�`�|�{���͐����`�ł����|�̖ʐ�)������������A�����������A�Ȑ��F
�̕����ɑ��݂���l�p�`�|�{���͐����`�ł����|�̖ʐ�)������������A�����������A�Ȑ��F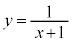 ��y���Cx���C����
��y���Cx���C����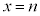 �Ƃň͂܂�镔���̖ʐ�B�����傫�����Ƃ́A�}������킩��܂��B�]���āA
�Ƃň͂܂�镔���̖ʐ�B�����傫�����Ƃ́A�}������킩��܂��B�]���āA
�Ƃ����s�����������ɍ�邱�Ƃ��ł��܂��B��w�����̓��ĂƂ��ẮA�E�}�������ď�L�̂悤�ɐ�������Ώ[���ł����A�����ł́A�����������J�ɏ����Ă݂܂��B
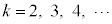 �Ƃ��āA
�Ƃ��āA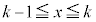 ����x�ɂ��āA
����x�ɂ��āA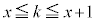 ���������܂��B���̂Ƃ��A
���������܂��B���̂Ƃ��A
�e�ӂɐϕ��L�������Ă��s�����̌����͕ς��Ȃ�(��ϕ��ƕs�������Q��)�̂ŁA
�����ŁA
�ł��B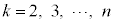 �ɂ��Ęa���Ƃ�ƁA
�ɂ��Ęa���Ƃ�ƁA
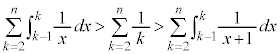 �@����@
�@����@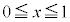 �ɂ����ẮA
�ɂ����ẮA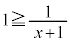 ���A
���A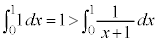
������A�@�̍��ӂƒ��ӂɂ́A1�������A�E�ӂɂ�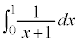 �������Ă��s�����͐������܂��B
�������Ă��s�����͐������܂��B
���D�Ȃ��A����Ȗʓ|�Ȃ��Ƃ����邩�ƌ����ƁA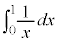 ���v�Z�ł��Ȃ�����ł��B
���v�Z�ł��Ȃ�����ł��B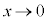 �̂Ƃ��A
�̂Ƃ��A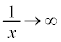 �ƂȂ��Ă��܂��܂��B
�ƂȂ��Ă��܂��܂��B ������A
�͂��݂����̌������A
�ł��邱�Ƃ��킩��܂��B
�ȏ�Ɠ��l�ɂ��āA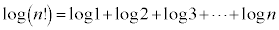 �ɂ��Ă����ׂ邱�Ƃ��ł��܂��B
�ɂ��Ă����ׂ邱�Ƃ��ł��܂��B
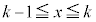 �̂Ƃ��A
�̂Ƃ��A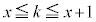 ���A
���A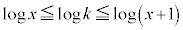
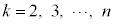 �ɂ��Ęa���Ƃ�ƁA
�ɂ��Ęa���Ƃ�ƁA
���̕s�����̒��ӂ́A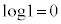 �Ȃ̂ŁA
�Ȃ̂ŁA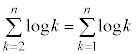 �Ƃł��܂��B����āA
�Ƃł��܂��B����āA
����āA�͂��݂����̌������A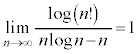
������n���\���ɑ傫���Ƃ��A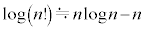 (�X�^�[�����O�̌���)
(�X�^�[�����O�̌���)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 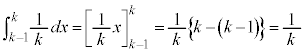
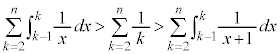 �@����@
�@����@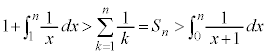
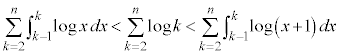
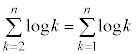 �Ƃł��܂��B����āA
�Ƃł��܂��B����āA